Диаграмма Хассе с примерами

Сразу хочу сказать, что здесь никакой воды про диаграмма хассе, и только нужная информация. Для того чтобы лучше понимать что такое диаграмма хассе , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

диаграмма хассе (xasse diagramma, Hasse diagram)— вид диаграмм, используемый для представления конечного частично упорядоченного множества в виде рисунка его транзитивного сокращения. Конкретно, для частично упорядоченного множества диаграмма представляет каждый элемент как вершины на плоскости и отрезки или кривые, идущие вверх от элемента к элементу , если и не существует элемента , для которого . Эти кривые могут пересекаться, но не должны проходить через вершины, если только они не являются концами линии. Такая диаграмма с помеченными вершинами однозначно определяют частичный порядок.

Впервые систематически такого рода визуализация описана Биркгофом в 1948 году , им же дано название в честь использовавшего подобные диаграммы Хельмута Хассе, однако такого рода рисунки встречаются и в более ранних трудах, например, в учебнике французского математика Анри Фохта (нем. Henri Vogt) 1895 года издания .

Определение диаграммы Хассе.

Любое частично-упорядоченное мн-во можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости. Если элемент у покрывает элемент х, то х и у соединяются отрезком, причем точка х располагается ниже точки у. Такие схемы называют диаграммами Хассе.

Элемент у покрывает элемент х:

Пусть А ≠ ∅ и card A < ∞. Пусть p (подмножество А²) — отношение порядка. Элемент у покрывает элемент х, если у ≤ х и не существует u ∈ A (x < u < y).

Отношения частичного порядка, то есть рефлексивные, антисимметричные и транзитивные, на которые накладывают ряд дополнительных свойств, изучаются в рамках раздела математики с экзотическим названием ТЕОРИЯ РЕШЕТОК. Это название пугает, поэтому в нашей стране первоначально слово lattice переводили как "структура". Но когда в математике все шире стал употребляться термин structure, то пришлось ему отдать русское слово структура, а решетки стали и у нас в стране решетками.
Можно предположить, что название "решетки" возникло в связи с использованием так называемых диаграмм Хассе3, которые напоминают экстравагантные решетки для окон...
Начнем с примеров решеток.
Возьмем слова: о, ор, вор, ворот, кол, олово, коловорот - и упорядочим их по вхождению одних слов в другие (не забывая, что каждое слово входит само в себя). Это будет наша первая решетка.
Можно убедиться, что здесь выполняются все свойства частичного порядка. А о дополнительных свойствах поговорим позже.
Числа: 1, 2, 3, 4, 6, 9, 12, 18, 36 с отношением «делить нацело» так же образуют решетку.
Обычные действительные числа с отношением "больше или равно" дают одну из самых распространенных решеток. Хотя для нас она менее экзотическая. Можно сказать, простая как бревно...
Множество всех подмножеств какого-то множества с отношением включения дает решетку, причем, с рядом замечательных свойств.

Отношения, похожие на отношения порядка, но не обладающие свойством транзитивности, называют отношениями ТОЛЕРАНТНОСТИ.
Хорошей иллюстрацией этого отношения служат многие известные картинки Эшера, где, например, птицы плавно превращаются в рыб и т.п.

Удобство диаграмм

Хотя диаграммы Хассе является простым и интуитивно ясным средством для работы с конечным частично упорядоченным множеством, весьма сложно нарисовать «хорошую», удобную для визуального восприятия диаграмму для достаточно нетривиального множества из-за большого количества возможных вариантов отображения. Простая техника, предполагающая начать с минимальных элементов и рисовать вышележащие элементы последовательно часто дает плохие результаты — симметрии и внутренние структуры легко потерять.

Например, булеан множества из четырех элементов, упорядоченного операцией включения может быть представлен любой из четырех нижеприведенных диаграмм (каждое подмножество снабжено меткой с бинарной кодировкой, показывающей, содержится соответствующий элемент в подмножестве — 1, или нет — 0):

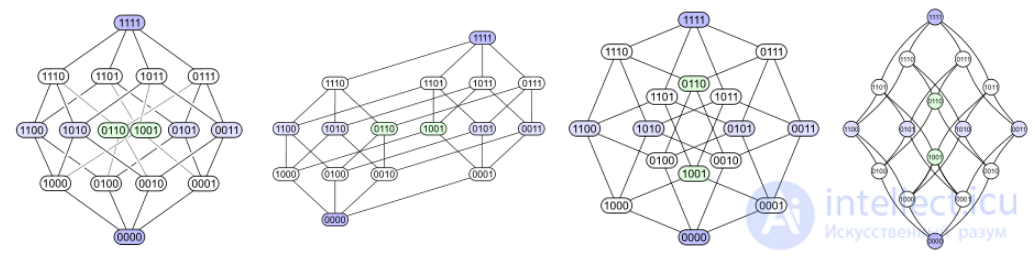
Первая диаграмма демонстрирует структуру уровней. Об этом говорит сайт https://intellect.icu . Вторая диаграмма имеет ту же структуру уровней, но на ней некоторые ребра удлинены, чтобы подчеркнуть, что четырехмерный куб является объединением двух трехмерных. Третья диаграмма показывает некоторую внутреннюю симметрию. В четвертой диаграмме вершины упорядочены подобно матрице 4×4.

Планарность

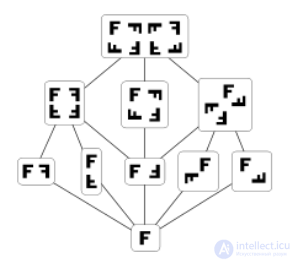
Диаграмма Хассе подгрупповой решетки диэдрической группы не имеет пересекающихся ребер.

Некоторые свойства частичных порядков относительно планарности их диаграммы Хассе (то есть возможности нарисовать ее без пересечения ребер):

• Если частичный порядок является решеткой, то его можно нарисовать без пересечений тогда и только тогда, когда размерность порядка не менее двух .
• Если частичный порядок имеет по меньшей мере один минимальный или максимальный элемент, то можно за линейное время проверить, существует ли диаграмма без пересечений .
• Определить, можно ли частичный порядок представить планарной диаграммой Хассе, в общем случае NP-полная задача .
• Если заданы -координаты элементов частичного порядка, то за линейное время может быть найдена его диаграмма Хассе, сохраняющая заданные координаты, если только такая диаграмма существует . В частности, если частный порядок имеет уровни, можно за линейное время определить, имеется ли диаграмма Хассе без пересечений, у которой высота каждой вершины пропорциональна ее рангу.

Определения

Наибольший (Величайший) и Наименьший элемент. Наименьший элемент диаграммы является тем элементом, который начинает диаграмму, а наибольшим (величайшим), тем элементом, который ее заканчивает. Причем если наибольших (величайших) или наименьших элементов несколько, то в ответ будет записываться, что наибольшего или наименьшего элемента нет. Другими словами, наибольший (величайший) и наименьший элемент на диаграмме Хассе — только один.

Возвращаясь к первому примеру, там сразу видно, что наименьшим элементом у нас будет Ø, а наибольшим (величайшим) {3;6;4}. Во втором примере наименьшим элементом будет 1, а наибольшего (величайшего) элемента не будет, т.к. наибольшими (величайшим) элементами могут быть сразу 4 и 10, следовательно, наибольшего (величайшего) элемента во втором примере нет.

Максимальные элементы — это те, которые не заменяются другим элементом. Минимальные элементы — это те, которым не предшествует другой элемент.

Нотация UML

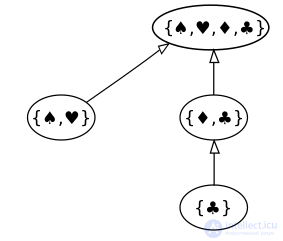
Выражение примера с помощью стандартных соединителей наследования UML. Каждый набор представляет собой отдельный объект (стандартные блоки UML имеют прямоугольную форму).

Стандартная диаграмма для цепочки включений - это класс UML , связывающий множества отношением наследования. На рисунке показан вложенный набор сбора , C :

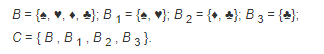
В программной инженерии классы программной системы и отношения наследования между этими классами часто изображаются с помощью диаграммы классов , формы диаграммы Хассе, в которой ребра, соединяющие классы, нарисованы в виде сегментов сплошной линии с незамкнутым треугольником на конце суперкласса. .

Диаграмма классов , изображающая множественное наследование

Примеры

пример 1

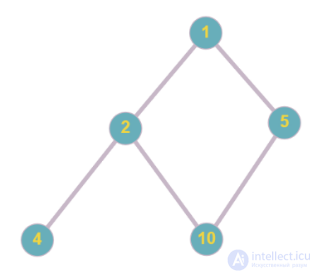
Рис.1 Диаграмма Хассе для второго отношения

Построим диаграмму Хассе для отношения Ω, где Ω: быть делителем.

Возьмем множество A = {1;2;4;5;10}. Построенная диаграмма показана на Рис. 1.

пример 2

Возьмем некоторое множество A = {3;6;4} и построим отношение ƿ, где ƿ: P(A) x P(A). P(A) – множество всех подмножеств, его можно представить в таком виде: { Ø, {3}, {6}, {4}, {3;6}, {6;4}, {3;4}, {3;6;4}}. Построим диаграмму Хассе данного отношения. На Рисунке 2, приведена эта диаграмма.

Отметим, что в этой диаграмме один элемент “Покрывает” другой, то есть, если мы берем два случайных элемента, то они не равны друг – другу и одни из этих элементов предшествует другому. К примеру, возьмем из диаграммы элемент Ø и {3}, они не равны друг – другу и один предшествует другому.

Еще одним свойством диаграммы Хассе является то, что из любой части диаграммы можно добраться в любую другую

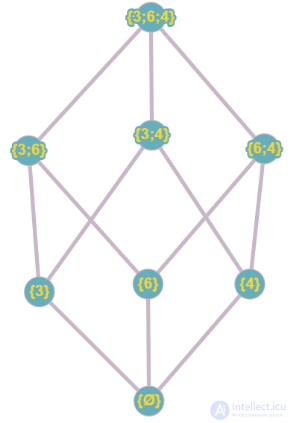
Рис.2 Диаграмма Хассе для отношения

пример 3

Булеан ( англ. power set , нем. potenzmenge ) — в теории множеств , это множество всех подмножеств данного множества �, сказывается�(�) или 2�(поскольку она соответствует множеству отражений с � в 2={0,1}).

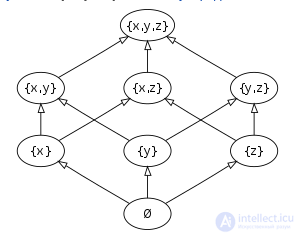
Булеан of { x , y , z } частично упорядочен по включению :

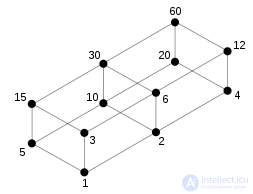
Множество A = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60} всех делителей числа 60, частично упорядочено по делимости :

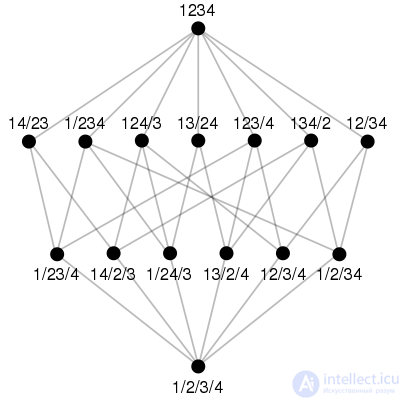
Множество всех 15 разбитий множества { 1, 2, 3, 4 }, где более грубое разбиение выше более мелкого:

Пример 7.

Пусть созвездие Рака представляет собой диаграмму Хассе отношения частичного порядка.

Перечислите упорядоченные пары отношения и найдите его двоичную матрицу.

Решение.

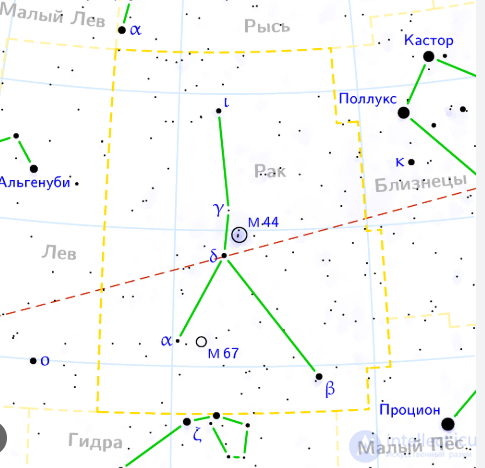
Рассмотрим множествоB={α,β,δ,γ,ι}.Элементы множества обозначают звезды в созвездии. Поскольку данное отношение является частичным порядком, оно должно обладать тремя свойствами: рефлексивностью, антисимметрией и транзитивностью. Поэтому оно содержит следующие упорядоченные пары:

(α,α),(α,δ),(α,γ),(α,ι),(β,β),(β,δ),(β,γ),(β,ι),(δ,δ),(δ,γ),(δ,ι),(γ,γ),(γ,ι),(ι,ι).

Отношение частичного порядка можно легко преобразовать в матричное представление:

Применение Диаграмм Хассе

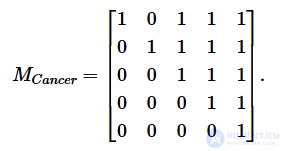
Диаграмма Хассе имеет широкое применение в различных областях, особенно в теории частично упорядоченных множеств. Вот некоторые примеры применения диаграммы Хассе:

1. Теория решеток: Диаграммы Хассе активно используются в теории решеток для изучения и визуализации структуры решеток и их свойств. Они позволяют наглядно представить отношение порядка и структуру элементов в решетке.

2. Таксономия и классификация: Диаграммы Хассе часто применяются в таксономии и классификации для организации и визуализации отношений между различными категориями или классами. Они помогают понять иерархическую структуру и взаимосвязи между различными понятиями.

3. Анализ данных: В анализе данных диаграммы Хассе могут использоваться для визуализации иерархии или иерархических отношений между данными или переменными. Они могут помочь исследователям лучше понять структуру данных и их связи.

4. Логика и алгебра: Диаграммы Хассе также находят применение в логике и алгебре. Они используются для визуализации и изучения структуры алгебраических систем, таких как булевы алгебры и алгебры множеств.

5. Исследование порядка: Диаграммы Хассе являются мощным инструментом для исследования отношений порядка и свойств частично упорядоченных множеств. Они позволяют выявить минимальные и максимальные элементы, цепи, антицепи и другие свойства структуры.

Это лишь некоторые примеры применения диаграммы Хассе. Ее гибкость и интуитивная наглядность делают ее полезным инструментом в различных областях, где необходимо визуализировать и анализировать структуру и отношения между элементами.

Вау!! 😲 Ты еще не читал? Это зря!

• Карты Карно
• Окружности Вилларсо
• диаграмма венна , диаграмма эйлера ,
• диаграмма Венна
• Теория множеств
• теория решеток
• отношения ПОРЯДКА
• круги Эйлера
• Карта Карно
• Окружности Вилларсо
• Диаграмма паука ( унитарная паутинная диаграмма)

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про диаграмма хассе Надеюсь, что теперь ты понял что такое диаграмма хассе и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.