Лекция
Привет, Вы узнаете о том , что такое толщина графа, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое толщина графа, род графа, укладка графа на торе , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Родом графа (англ. genus) g(G) обозначается наименьшее количество ручек, которое необходимо добавить к сфере, чтобы граф был уложен на этой поверхности без пересечений.
Для планарных графов g = 0,
для графа К5 g = 1.
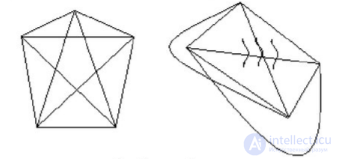
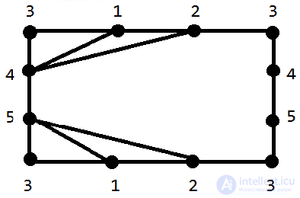
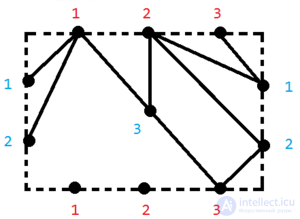
Если нужно, чтобы данный на рисунке граф был без пересечений нужна 1 ручка.
При проектировании транспортных сетей встает задача об укладке графа на плоскости, но не каждый граф планарен. Если сеть представляет из себя непланарный граф, то придется делать перекрестки или строить мосты. Постройка мостов обойдется дороже постройки обычной дороги, а перекрестки увеличивают время поездки. Поэтому перед началом работы будет полезно вычислить род, толщину, крупность и число срещиваний графа.
Графы К5, К3,3, К4,4, К7 - тороидальные графы, то есть у них род g = 1.
Для любой поверхности имеется конечный набор графов,
который ее характеризует, то есть тех графов, которые
нельзя уложить на данной поверхности.
Обобщение ТЕОРЕМЫ Эйлера на графы рода g.
Пусть дан G(p, q), имеющий f-граней, то для него справедливо: p + f - q = 2 - 2g
СЛЕДСТВИЕ 1. Для любого связанного графа с р-вершинами и q-ребрами, причем р 4, справедливо:
g = ] (q - 3p + 1)/6 [
СЛЕДСТВИЕ 2. Для полных графом справедливо
g(Kp) = ] (p - 3)(p - 4)/12 [
толщина графа (англ. thickness) - это минимальное количество планарных подграфов графа G, таких что их объединение дает граф G.
Известно, что толщина полных графов равна
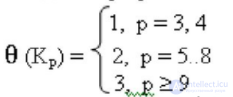
Так как в планарном графе q = 3p - 6, то 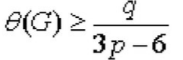
Так как в полном графе q = p(p - 1)/2, то 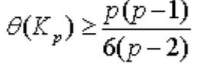
По определению, если существует набор k планарных графов, имеющих одинаковый набор вершин, объединение которых дает граф G , то толщина графа G не больше k . Таким образом, планарный граф имеет толщину 1 . Графы с толщиной 2 называются двупланарными графами. Концепция толщины возникла в гипотезе Фрэнка Харари: любой граф с 9 вершинами либо сам, либо его дополнение, является непланарным. Эта гипотеза верна, так как полный граф K9 не является бипланарным.
Толщина полного графа θ(Kn)=⌊n+76⌋ но толщина графов K9 и K10 равна 3 .
ТЕОРЕМА (о степенях вершин в планарном графе).
В любом планарном графе существует вершина, степень которой не больше 5.
Доказательство:
Допустим, такой вершины нет, тогда
степень каждой вершины не меньше 6, следовательно,
6р <= 2q, то есть q >=3p.
Но для планарных графов
q <=3p - 6.
Получили противоречие.
| Определение: |
| Крупностью (англ. Об этом говорит сайт https://intellect.icu . coarseness) ξ графа G называется наибольшее число непланарных графов в G , не пересекающихся по ребрам. |
Формулы для вычисления крупности полного графа не такие простые, как для других топологических инвариантов.
Крупность планарного графа равна 0 , так как планарный граф не может содержать непланарный подграф.
Крупность ξ(K5)=1 и ξ(K3,3)=1 , так как K5 и K3,3 содеражат только один непланарный подграф.
| Определение: |
| Числом скрещиваний (англ. crossing number) ν графа G называется наименьшее число пересечений ребер, которое будет при укладке G на плоскости. |
Точное значения числа скрещиваний не известно, установлена только верхняя оценка.
Число скрещиваний полного графа ν(Kn)⩽14⌊n2⌋⌊n−12⌋⌊n−22⌋⌊n−32⌋
Число скрещиваний полного двудольного графа ν(Kn,m)⩽⌊n2⌋⌊n−12⌋⌊m2⌋⌊m−12⌋
Укладу планарного графа можно сделать с помощью гамма-алгоритма, где число скрещиваний будет равно 00.
| Определение: |
| Если граф можно уложить на торе, то он тороидальный. |
Тороидальный граф G имеет род γ(G)⩽1
Исследование, описанное в статье про толщина графа, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое толщина графа, род графа, укладка графа на торе и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про толщина графа
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.