Перестановки сочетания и размещения и бином Ньютона примеры кратко

Привет, сегодня поговорим про перестановки, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое перестановки, сочетания, размещения , бином ньютона , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Для формулирования и решения задач по комбинаторике используют следующие конфигурации: перестановки , размещения , сочетания .

Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до n, где n - число элементов множества.

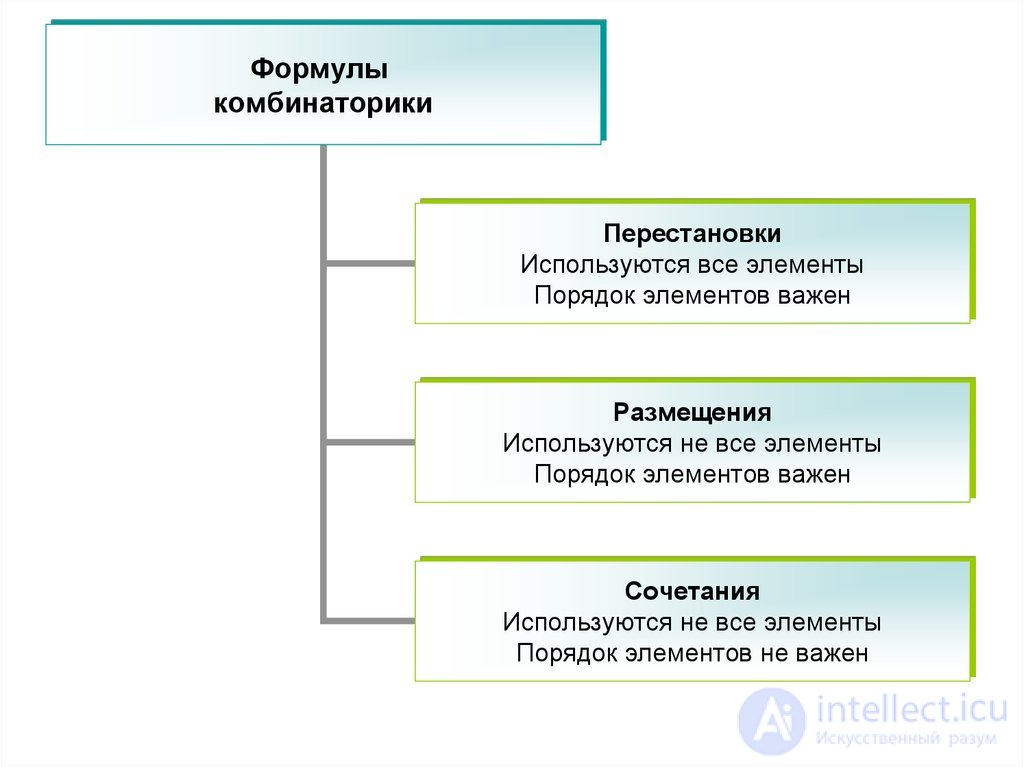
Внизу приведены все формулы и примеры когда их нужно применять

Перестановка.

Пусть мы имеем некое упорядоченное множество N состоящее из n различных элементов. Перестановкой из n элементов называется такой набор элементов множества, которые отличаются от исходного лишь порядком элементов. Обычно перестановка обозначается как Pn и рассчитывается по формуле:

Pn = n!

Пример:

Найти число перестановок множества, состоящего из трех элементов: A, B, C.

Согласно формуле, количество перестановок будет равно 3! = 6.

Действительно, это наборы (ABC),(ACB),(BAC),(BCA),(CAB),(CBA).

Размещение.

Пусть мы имеем некое упорядоченное множество N состоящее из n различных элементов. Размещением из n элементов по k будет называться упорядоченное подмножество из k не повторяющихся элементов выбранные из множества, состоящего изn элементов. Обычно размешение обозначается как A_n^k и рассчитывается по формуле:

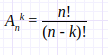
Пример:

Найти число размещений множества, состоящего из четырех элементов: A, B, C, D по два, т.е. Об этом говорит сайт https://intellect.icu . сколько различных размещений по два элемента можно составить из указанного множества.

Согласно формуле, количество размещений будет равно 4!/(4-2)! = 24/2 = 12.

Действительно, это наборы (AB),(BA),(AC),(CA),(AD),(DA),(BC),(CB),(BD),(DB),(CD),(DC).

Сочетание.

Пусть мы имеем некое упорядоченное множество N состоящее из n различных элементов. Сочетанием из n элементов по k будет называться подмножество из k не повторяющихся элементов выбранные из множества, состоящего из n элементов. Подмножества, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений. Обычно сочетание обозначается как 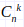и рассчитывается по формуле:

Пример:

Найти число сочетаний множества, состоящего из четырех элементов: A, B, C, D по два.

Согласно формуле, количество сочетаний будет равно 4!/2!(4-2)! = 24/4 = 6.

Действительно, это наборы (AB),(AC),(AD),(BC),(BD),(CD).

Свойства сочетаний:

1. С_n⁰ = 1.

2. С_n^k = С_n^{n - k}.

3. С_n^k = С_{n - 1}^{k - 1} + С_{n - 1}^k

4. С_n⁰ + С_n¹ + С_n² + ... + С_n^{n - 1} + С_nⁿ = 2ⁿ.

Сочетание играет важную роль в математике. В частности, он используется в биноме Ньютона.

бином ньютона .

Бином Ньютона - это отношение, позволяющая представить выражение (a + b)n (n ∈ Z+) в виде многочлена, а именно:

(a + b)ⁿ = aⁿ + С_n¹a^{n - 1}b + С_n²a^{n - 2}b² + ... + С_n^ka^{n - k}b^k + ... + С_n^{n - 1}ab^{n - 1} + bⁿ.

Числа С_n¹, С_n², ... , С_n^{n - 1} называются биномиальными коэффициентами.

С помощью следующей таблицы можно определить значения биномиальных коэффициентов для любой степени. Строится он следующим образом - любое число образуется суммой рядом стоящих чисел над ним.

Это стало причиной тому что данная таблица называется треугольник Паскаля.

Слева указана степень n, справа значения соответствующих биномиальных коэффициентов.

Пример:

Представить в виде многочлена (a + 1)4.

Согласно таблице, в случае четвертой степени коэффициенты результирующего многочлена будут равны 1, 4, 6, 4, 1.

И, действительно (a + 1)4 = a4 + 4a3 + 6a2 + 4a + 1.

Сводка формул для всех видов перестановок

Вау!! 😲 Ты еще не читал? Это зря!

• перестановки , сочетания , размещения , перестановки с повторениями ,
• сводка формул для всех видов соединений , комбинаторика , перестановки , размещения с повторениями ,

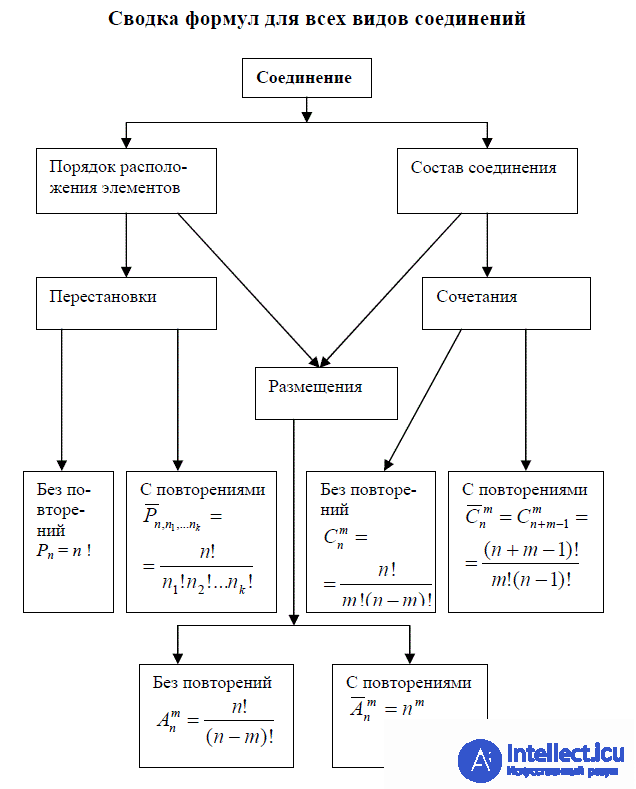
На этом все! Теперь вы знаете все про перестановки, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое перестановки, сочетания, размещения , бином ньютона и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Из статьи мы узнали кратко, но содержательно про перестановки