Блоковый граф (кликовое дерево) и Связанные классы графов кратко

Привет, Вы узнаете о том , что такое блоковый граф, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое блоковый граф, кликовое дерево, связанные классы графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

блоковый граф ( кликовое дерево ) — вид неориентированного графа, в котором каждая компонента двусвязности (блок) является кликой .Блоковые графы можно описать графами пересечений блоков произвольных неориентированных графов.

Кликой неориентированного графа называется подмножество его вершин, любые две из которых соединены ребром. Клики являются одной из основных концепций теории графов и используются во многих других математических задачах и построениях с графами. Клики изучаются также в информатике — задача определения, существует ли клика данного размера в графе (Задача о клике) является NP-полной. Несмотря на эту трудность, изучаются многие алгоритмы для поиска клик.

Блоковый граф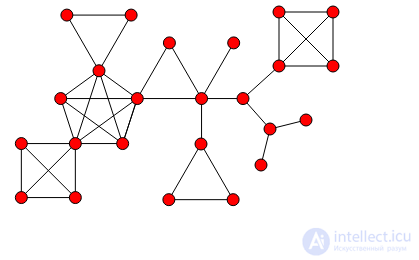

Описание

Блоковые графы — это в точности те графы, в которых для каждых четырех вершин , и наибольшие два из трех расстояний , , всегда равны^[

Их можно также описать с помощью запрещенных подграфов, как графов, не содержащих алмазов или циклов длины четыре или более в качестве порожденного подграфа. Об этом говорит сайт https://intellect.icu . То есть, они являются хордальными графами без алмазов . Они являются также графами Птолемея (хордальными дистанционно-наследуемыми графами ), в которых любые две вершины на расстоянии два соединены единственным кратчайшим путем, и хордальными графами, в которых любые две клики имеют максимум одну общую вершину.

Граф является блоковым тогда и только тогда, когда пересечение любых двух связных подмножеств вершин графа либо пусто, либо связно. Таким образом, связные подмножества вершин в связном блоковом графе образуют выпуклую геометрию^[en], и этим свойством не обладает никакой другой вид графов По причине этого свойства в связном блоковом графе любое множество вершин имеет единственное минимальное связное надмножество, замыкание множества в выпуклой геометрии. Связные блоковые графы — это в точности те графы, в которых существует единственный порожденный путь, соединяющий любые две пары вершин .

связанные классы графов

Блоковые графы являются хордальными и дистанционно-наследуемыми графами. Дистанционно-наследуемые графы — это графы, в которых любые два порожденных пути между двумя вершинами имеют одну и ту же длину, что слабее требования блоковых графов как имеющих единственный порожденный путь между любыми двумя вершинами. Поскольку и хордальные графы, и дистанционно-наследуемые графы являются подклассами совершенных графов, блоковые графы тоже совершенны.

Любое дерево является блоковым графом. Другой пример класса блоковых графов дают мельницы.

Любой блоковый граф имеет прямоугольность, не превосходящую двух

Блоковые графы являются примером псевдо-медианных графов — для любых трех вершин либо существует единственная вершина, лежащая на трех кратчайших путях между этими тремя вершинами, либо существует единственный треугольник, ребра которого лежат на этих кратчайших путях.

Реберные графы деревьев — это блоковые графы, в которых любая разрезающая вершина инцидентна максимум двум блокам, или, что то же самое, блоковые графы без клешней. Реберные графы деревьев используются для поиска графов с заданным числом ребер и вершин, в котором наибольший порожденный подграф, являющийся деревом как можно меньшего размера

Блоковые графы неориентированных графов

Блоковый граф для заданного графа (обозначается ) — граф пересечений блоков графа : имеет вершину для каждой двусвязной компоненты графа и две вершины графа смежны, если соответствующие два блока разделяют (имеют общий) шарнир (в терминах Харари — точка сочленения). Если — граф с одной вершиной, то по определению будет пустым графом. заведомо является блочным — он имеет одну двусвязную компоненту для каждой точки сочленения графа и каждая двусвязная компонента, образованная таким путем, будет кликой. Обратно, любой блоковый граф является графом для некоторого . Если — дерево, то совпадает с реберным графом графа .

Граф имеет вершину для каждой точки сочленения графа . Две вершины смежны в , если они принадлежат одному и тому же блоку в

Вау!! 😲 Ты еще не читал? Это зря!

• рёберный граф , производный граф , покрывающий граф ,
• Флаговый комплекс
• клика

Исследование, описанное в статье про блоковый граф, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое блоковый граф, кликовое дерево, связанные классы графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.