Лекция
Привет, сегодня поговорим про кограф, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое кограф, дополнительно сводимый граф, свободный от p граф , кодеревья, кодерево , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
В теории графов кограф , или дополнительно сводимый граф , или свободный от P4 граф — это граф, который можно получить из графа с единственной вершиной K1 путем операций дополнения и объединения графов. Таким образом, семейство кографов — это наименьший класс графов, содержащий K1 и замкнутый относительно дополнения и объединения.
Кографы открывались независимо несколькими авторами, начиная с 1970-х годов. Самые ранние упоминания можно найти у Янга(Jung 1978), Лерчса (Lerchs 1971), Зайнше (Seinsche 1974) и Самнера (Sumner 1974). Эти графы назывались D*-графами (Jung 1978), наследственными графами Дейси (после работы Джеймса Дейси (James C. Dacey, Jr.) об ортомодуляных решетках[en]. Смотрите работу Самнера (Sumner 1974)) и графы с двумя потомками Барлета и Ури (Burlet, Uhry 1984).
Смотрите книгу Брандштедта, Ли и Шпинрада (Brandstädt, Le, Spinrad 1999), где кографы рассмотрены более детально, включая факты, приведенные здесь.
Любой кограф можно построить, следуюя следующим правилам:
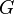 — кограф, то его дополнение
— кограф, то его дополнение 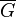 тоже кограф;
тоже кограф;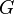 и
и 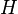 — кографы, то их несвязанное объединение
— кографы, то их несвязанное объединение 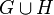 тоже кограф.
тоже кограф.Можно дать несколько других описаний кографов. Среди них:
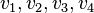 , если
, если 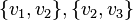 и
и 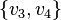 — ребра графа, то хотя бы одно из
— ребра графа, то хотя бы одно из 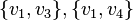 или
или 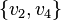 тоже является ребром (Corneil, Lerchs, Burlingham 1981).
тоже является ребром (Corneil, Lerchs, Burlingham 1981).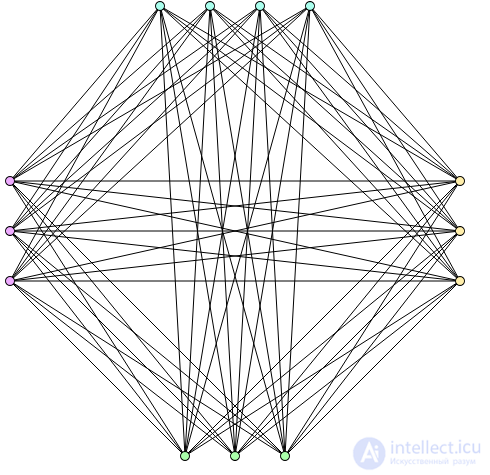
Граф Турана T(13,4) как пример кографа
Все полные графы, полные двудольные графы, пороговые графы и графы Турана являются кографами. Об этом говорит сайт https://intellect.icu . Любой кограф является дистанционно-наследуемымсовершенным графом сравнимости.
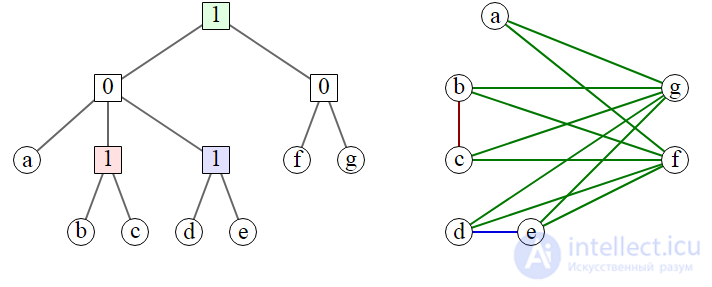
Кодеревья и соответствующие кографы. Каждое ребро (u,v) в кографе имеет соответствующий цвет ближайшего общего родителя вершин u и v в кодереве.
кодерево — это дерево, в котором внутренние вершины помечены числами 0 и 1. Любое кодерево Tопределяет кограф G, имеющий листья кодерева T в качестве вершин, а поддерево, имеющее корень в вершине T, соответствует порожденному подграфу в G, определенному множеством листьев-потомков этой вершины:
Эквивалентный путь построения кографа из кодерева заключается в том, что две вершины соединяются ребром в том и только в том случае, когда наименьший общий предок соответствующих листьев помечен 1. И наоборот, любой кограф можно представить кодеревом таким способом. Если потребовать, чтобы все метки на всех путах от корня к листьям чередовались, такое представление будет единственным (Corneil, Lerchs, Burlingham 1981).
Кограф можно распознать за линейное время и построить при этом представление в виде кодерева, если использовать модульное разложение[en] (Corneil, Perl, Stewart 1985), очистку разложения[en] (Habib, Paul 2005) или разложение расщеплением (Gioan, Paul 2008). Как только кодерево построено, многие знакомые задачи теории графов можно решить посредством прохода снизу вверх по кодереву.
Например, чтобы найти максимальную клику в кографе, вычисляем, проходя снизу вверх, максимальную клику в каждом подграфе, представленным поддеревом кодерева. Для каждой вершины с меткой 0 максимальная клика – это максимальная клика, полученная у потомков вершины. Для вершины с меткой 1 максимальная клика будет объединением клик, вычисленных для потомков вершины, а размер этой клики равен сумме размеров клик. Таким образом, попеременно беря максимальный размер и суммируя значения для каждой вершины кодерева, мы вычислим максимальный размер клики, а попеременно выбирая максимальную клику и объединяя, построим саму максимальную клику. Похожий подход прохода снизу вверх позволяет получить максимальное независимое множество, хроматическое число, максимальное кликовое покрытие и существование гамильтонового пути[en] за линейное время. Можно также использовать кодеревья для определения за линейное время являются ли два кографа изоморфными.
Если H — порожденный подграф кографа G, то H сам по себе является кографом. Кодерево для H можно получить удалением части листьев из кодерева для G с последующим слиянием вершин, имеющих единственного потомка. Из теоремы Крускала о деревьях[en] следует, что отношение быть порожденным подграфом является хорошим квазипорядком[en] на кографах (Damaschke 1990). Так, если семейство кографов (таких как планарные кографы) замкнуто относительно операции построения порожденного подграфа, то оно имеет конечное число запрещенных порожденных подграфов[en]. С точки зрения вычислений, это означает, что проверку, принадлежит ли граф такому семейству, можно выполнить за линейное время, если использовать проход снизу вверх по кодереву заданного графа.
На этом все! Теперь вы знаете все про кограф, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое кограф, дополнительно сводимый граф, свободный от p граф , кодеревья, кодерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.