Лекция
Привет, сегодня поговорим про среднеквадратическое отклонение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое среднеквадратическое отклонение , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространенный показатель рассеивания значенийслучайной величины относительно ее математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используетсясреднее арифметическое совокупности выборок.
среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчете стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.
Среднеквадратическое отклонение:
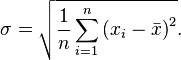
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно ее математического ожидания на основе несмещенной оценки ее дисперсии):
где 
— дисперсия; 
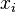— i-й элемент выборки; 
— объем выборки ;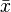 
— среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещенными. Об этом говорит сайт https://intellect.icu . В общем случае несмещенную оценку построить невозможно. Однако оценка на основе оценки несмещенной дисперсии является состоятельной.
Правило трех сигм (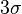
) — практически все значения нормально распределенной случайной величины лежат в интервале 
. Более строго — приблизительно с 0,9973 вероятностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина 
истинная, а не полученная в результате обработки выборки).
Если же истинная величина неизвестна, то следует пользоваться не 
, а s. Таким образом, правило трех сигм преобразуется в правило трех s.
Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трех множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределенности. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
На практике среднеквадратическое отклонение позволяет оценить, насколько значения в множестве могут отличаться от среднего значения.
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчета волатильности.
На этом все! Теперь вы знаете все про среднеквадратическое отклонение, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое среднеквадратическое отклонение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про среднеквадратическое отклонение
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.