14.2. Оценки для математического ожидания и дисперсии кратко

Привет, Вы узнаете о том , что такое оценки для ма тического ожидания, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое оценки для ма тического ожидания, дисперсии , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Пусть имеется случайная величина 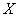 с математическим ожиданием  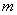и дисперсией 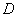; оба параметра неизвестны. Над величиной  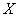произведено  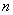независимых опытов, давших результаты 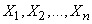. Требуется найти состоятельные и несмещенные оценки для параметров  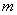и .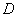

 

В качестве оценки для математического ожидания естественно предложить среднее арифметическое наблюденных значений (ранее мы его обозначали ):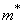

.                               (14.2.1)

Нетрудно убедиться, что эта оценка является состоятельной: согласно закону больших чисел, при увеличении 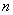 величина  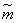сходится по вероятности к 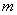. Оценка  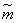является также и несмещенной, так как

.                (14.2.2)

Дисперсия этой оценки равна:

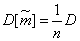.                          (14.2.3)

Эффективность или неэффективность оценки зависит от вида закона распределения величины 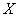. Можно доказать, что если величина  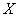распределена по нормальному закону, дисперсия (14.2.3) будет минимально возможной, т. е. оценка  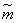является эффективной. Для других законов распределения это может быть и не так.

Перейдем к оценке для дисперсии 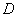 . Об этом говорит сайт https://intellect.icu . На первый взгляд наиболее естественной оценкой представляется статистическая дисперсия:

,               (14.2.4)

где

.                            (14.2.5)

Проверим, является ли эта оценка состоятельной. Выразим ее через второй начальный момент (по формуле (7.4.6) гл. 7):

.                 (14.2.6)

Первый член в правой части есть среднее арифметическое 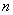 наблюденных значений случайной величины 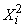; он сходится по вероятности к 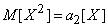. Второй член сходится по вероятности к 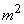; вся величина (14.2.6) сходится по вероятности к величине

.

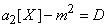Это означает, что оценка (14.2.4) состоятельна.

Проверим, является ли оценка 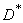 также и несмещенной. Подставим в формулу (14.2.6) вместо  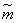его выражение (14.2.5) и произведем указанные действия:

.              (14.2.7)

Найдем математическое ожидание величины (14.2.7):

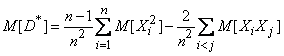.                      (14.2.8)

Так как дисперсия 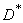 не зависит от того, в какой точке выбрать начало координат, выберем его в точке 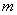. Тогда

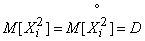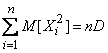;  ,   (14.2.9)

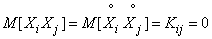.                            (14.2.10)

Последнее равенство следует из того, что опыты независимы.

Подставляя (14.2.9) и (14.2.10) в (14.2.8), получим:

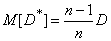.                  (14.2.11)

Отсюда видно, что величина 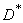 не является несмещенной оценкой для 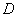: ее математическое ожидание не равно 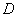, а несколько меньше. Пользуясь оценкой  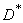вместо дисперсии 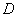, мы будем совершать некоторую систематическую ошибку в меньшую сторону. Чтобы ликвидировать это смещение, достаточно ввести поправку, умножив величину  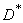на 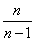. Получим:

.

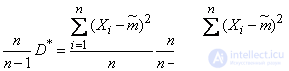Такую «исправленную» статистическую дисперсию мы и выберем в качестве оценки для :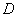

.                (14.2.12)

Так как множитель 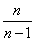 стремится к единице при 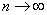, а оценка  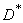состоятельна, то оценка  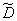также будет состоятельной.

На практике часто вместо формулы (14.2.12) бывает удобнее применять другую, равносильную ей, в которой статистическая дисперсия выражена через второй начальный момент:

.                   (14.2.13)

При больших значениях 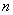, естественно, обе оценки - смещенная  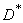и несмещенная  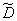- будут различаться очень мало и введение поправочного множителя теряет смысл.

Таким образом, мы пришли к следующим правилам обработки ограниченного по объему статистического материала.

Если даны значения 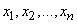, принятые в  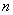независимых опытах случайной величиной  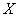с неизвестными математическим ожиданием  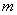и дисперсией 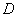, то для определения этих параметров следует пользоваться приближенными значениями (оценками):

                    (14.2.14)

Информация, изложенная в данной статье про оценки для ма тического ожидания , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое оценки для ма тического ожидания, дисперсии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про оценки для ма тического ожидания