Вопросы о корреляции для экзамена и тестов на собеседовании кратко

Привет, Вы узнаете о том , что такое Вопросы о корреляции для экзамена и тестов на собеседовании, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Вопросы о корреляции для экзамена и тестов на собеседовании , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Введение

Естественная траектория статистики обучения начинается с измерения центральной тенденции, за которой следует корреляция, регресс к другим продвинутым концепциям. Среди этих исходных концепций я обнаружил, что корреляцию легко понять, но я был озадачен, когда ее связали с другими статистическими концепциями и показателями, такими как причинно-следственная связь, регрессия, распределение, коэффициент корреляции Пирсона и т. Д. Мне потребовалось время, чтобы добиться успеха и прочно закрепиться по этой концепции. Мне это удалось, потому что я продолжал пытаться и старался изо всех сил каждый раз, когда у меня не получалось. Следовательно, не останавливайтесь, продолжайте попытки!

Для начала, если вы все еще пытаетесь понять разницу между корреляцией и причинно-следственной связью , вам следует обратиться к моей предыдущей статье, где я объяснил эти концепции самым простым из возможных способов.

Давайте продолжим и узнаем о наиболее часто задаваемых вопросах о корреляции. Если вы изучаете статистические концепции, вы обязательно столкнетесь с этими вопросами, которые в большинстве случаев люди стараются избегать. Для таких, как я, это должно стать хорошим напоминанием.

И если вы хотите узнать эти вопросы во время собеседования по науке о данных то потренеруйтесь на нижеприведенны вопрсах.

Что ты узнаешь?

1. Означают ли корреляция и зависимость одно и то же? Проще говоря, если корреляция двух событий равна нулю, означает ли это, что они не зависимы, и наоборот?
2. Если две переменные имеют высокую корреляцию с третьей переменной, означает ли это, что они также будут сильно коррелированы? Возможно ли вообще, что A и B положительно коррелируют с другой переменной C? Возможно ли, что А и В отрицательно коррелируют друг с другом?
3. Может ли единичный выброс значительно уменьшить или увеличить корреляцию? Очень ли чувствителен коэффициент Пирсона к выбросам?
4. Подразумевает ли причинная связь корреляцию?
5. В чем разница между корреляцией и простой линейной регрессией?
6. Как выбрать корреляцию Пирсона и Спирмена?
7. Как бы вы объяснили разницу между корреляцией и ковариацией?

Ответы на многие из приведенных выше вопросов могут показаться интуитивно понятными, однако в этой статье вы можете найти несколько неожиданных факторов, касающихся корреляции.

Давай начнем!

Понимание математической формулировки коэффициента корреляции

Наиболее широко используемый коэффициент корреляции - коэффициент Пирсона. Вот математическая формула для получения коэффициента Пирсона.

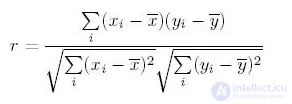
Объяснение: Это просто отношение ковариации двух переменных к произведению дисперсии (переменных). Принимает значение от +1 до -1. Экстремальное значение с обеих сторон означает, что они сильно коррелированы друг с другом. Нулевое значение указывает на корреляцию NIL, но не на независимость. Вы ясно поймете это в одном из следующих ответов.

Ответ - 1: корреляция против зависимости

Отсутствие зависимости между двумя переменными означает нулевую корреляцию. Однако обратное неверно. Нулевая корреляция может иметь даже идеальную зависимость. Об этом говорит сайт https://intellect.icu . Вот пример:

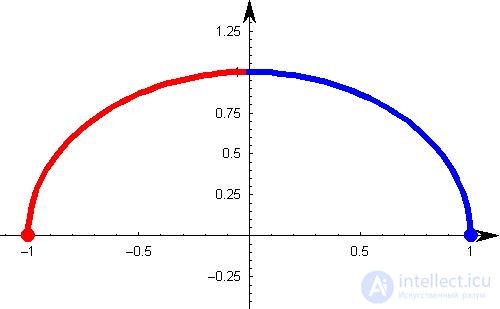
В этом сценарии, где квадрат x линейно зависит от y (зависимая переменная), все справа от оси y отрицательно коррелировано, а слева положительно коррелировано. Итак, каков будет коэффициент корреляции Пирсона?

Если вы сделаете математику, вы увидите нулевую корреляцию между этими двумя переменными. Что это значит? Для пары переменных, которые полностью зависят друг от друга, также можно получить нулевую корреляцию.

Следует помнить совет: корреляция количественно определяет линейную зависимость двух переменных. Он не может зафиксировать нелинейную связь между двумя переменными.

Хорошее чтение: необходимо прочитать книги по аналитике / науке о данных

Ответ - 2: корреляция транзитивна?

Предположим, что X, Y и Z - случайные величины. X и Y положительно коррелированы, а Y и Z также положительно коррелированы. Следует ли из этого, что X и Z должны быть положительно коррелированы?

Как мы увидим на примере, ответ (возможно , удивительно) « N о .» Мы можем доказать, что если корреляции достаточно близки к 1, то X и Z должны быть положительно коррелированы.

Предположим, C (x, y) - коэффициент корреляции между x и y. Аналогично у нас есть C (x, z) и C (y, z). Вот уравнение, которое получается из математического решения уравнения корреляции:

C (x, y) = C (y, z) * C (z, x) - квадратный корень ((1 - C (y, z) ^ 2) * (1 - C (z, x) ^ 2))

Теперь, если мы хотим, чтобы C (x, y) было больше нуля, мы в основном хотим, чтобы правая часть приведенного выше уравнения была положительной. Следовательно, вам необходимо решить:

 C (y, z) * C (z, x)> квадратный корень ((1 - C (y, z) ^ 2) * (1 - C (z, x) ^ 2))

Фактически мы можем решить указанное выше уравнение для обоих C (y, z)> 0 и C (y, z) <0 вместе, возведя обе стороны в квадрат. В конечном итоге это даст результат, поскольку C (x, y) - ненулевое число, если выполняется следующее уравнение:

С (у, г) ^ 2 + С (г, х) ^ 2> 1

Вау, это уравнение круга. Следовательно, следующий сюжет все объяснит:

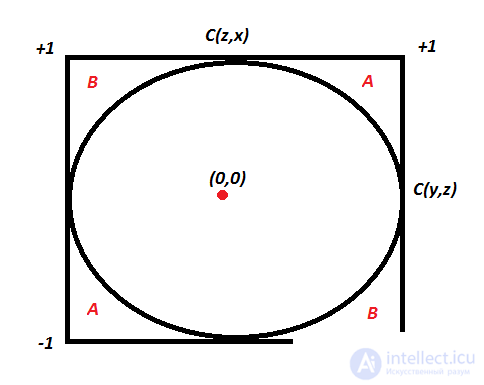
Если две известные корреляции находятся в зоне A, третья корреляция будет положительной. Если они лежат в зоне B, третья корреляция будет отрицательной. Внутри круга мы ничего не можем сказать об отношениях. Очень интересный вывод заключается в том, что даже если C (y, z) и C (z, x) равны 0,5, C (x, y) на самом деле также может быть отрицательным.

Ответ - 3: Чувствителен ли коэффициент Пирсона к выбросам?

Ответ - да. Даже один выброс может изменить направление коэффициента. Вот несколько случаев, каждый из которых имеет одинаковый коэффициент корреляции 0,81:

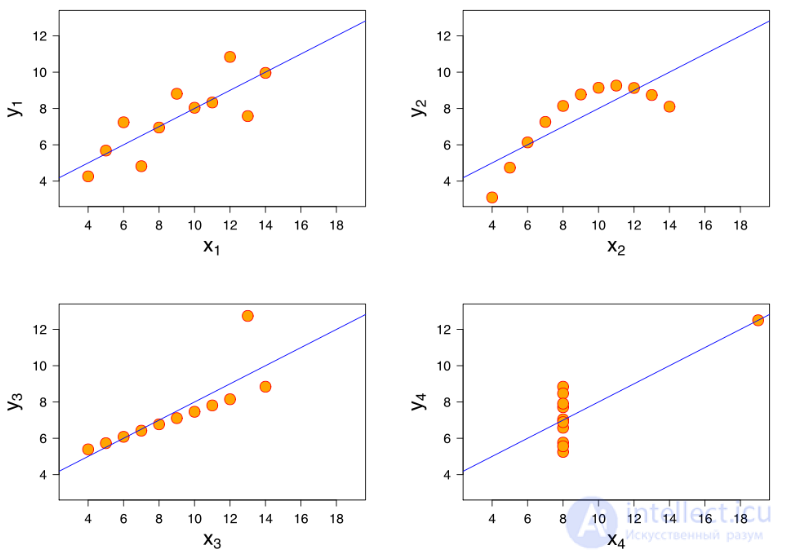
Рассмотрим два последних графика (X 3Y3 и X 4Y4). X3Y3 - это, несомненно, случай идеальной корреляции, когда один выброс значительно снижает коэффициент. Последний график полностью противоположен, коэффициент корреляции становится большим положительным числом из-за единственного выброса. В конечном итоге это оказывается самой большой проблемой для коэффициента корреляции, на него сильно влияют выбросы.

Проверьте свой потенциал: стоит ли мне стать специалистом по данным?

Ответ - 4: Подразумевает ли причинная связь корреляцию?

Если вы прочитали три приведенных выше ответа, я уверен, что вы сможете ответить на этот вопрос. Ответ - нет, потому что причинно-следственная связь также может привести к нелинейным отношениям. Давайте разберемся как!

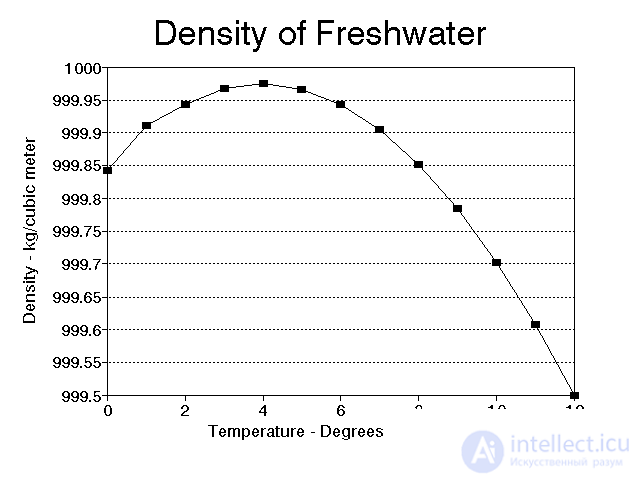
Ниже приведен график, показывающий плотность воды от 0 до 12 градусов Цельсия. Мы знаем, что плотность - это эффект изменения температуры. Но плотность может достигать максимального значения при 4 градусах Цельсия. Следовательно, она не будет линейно коррелировать с температурой.

Ответ - 5: разница между корреляцией и простой линейной регрессией

Эти двое действительно близки. Итак, давайте начнем с нескольких общих черт.

• Квадрат коэффициента корреляции Пирсона такой же, как и в простой линейной регрессии.
• Ни простая линейная регрессия, ни корреляция напрямую не отвечают на вопросы о причинной связи. Это важный момент, потому что я встречал людей, думающих, что простая регрессия может волшебным образом сделать вывод, который вызывает X. Это абсурдное мнение.

В чем разница между корреляцией и простой линейной регрессией?

Теперь давайте подумаем о нескольких различиях между ними. Простая линейная регрессия дает гораздо больше информации о взаимосвязи, чем корреляция Пирсона. Вот несколько вещей, которые дает регрессия, а коэффициент корреляции - нет.

• Наклон линейной регрессии дает предельное изменение выходной / целевой переменной путем изменения независимой переменной на единицу расстояния. Корреляция не имеет наклона.
• Перехват в линейной регрессии дает значение целевой переменной, если одна из входных / независимых переменных установлена ​​в ноль. Корреляция не имеет этой информации.
• Линейная регрессия может дать вам прогноз с учетом всех входных переменных. Корреляционный анализ ничего не предсказывает.

Ответ - 6: Пирсон против Спирмена

Самый простой ответ здесь - Пирсон фиксирует, насколько линейно зависимы две переменные, тогда как Спирмен фиксирует монотонное поведение отношения между переменными.

Например, рассмотрим следующие отношения:

у = ехр (х)

Здесь вы обнаружите, что коэффициент Пирсона равен 0,25, а коэффициент Спирмена равен 1. Как правило, вы должны начинать со Спирмена только тогда, когда у вас есть некоторая первоначальная гипотеза о нелинейности отношения. В противном случае мы обычно сначала пробуем Пирсона, а если мало, то Спирмена. Таким образом, вы узнаете, связаны ли переменные линейно или просто имеют монотонное поведение.

Ответ - 7: Корреляция против ковариации

Если вы пропустили математическую формулу корреляции в начале этой статьи, сейчас самое время вернуться к ней.

Корреляция - это просто нормализованная ковариация со стандартным отклонением обоих факторов. Это сделано для того, чтобы получить число от +1 до -1. Ковариацию очень сложно сравнивать, поскольку она зависит от единиц измерения двух переменных. Может оказаться, что оценки студента больше связаны с его ногтем на ноге в мили-метрах, чем с его посещаемостью.

Это просто из-за разницы в единицах измерения второй переменной. Следовательно, мы видим необходимость нормализовать эту ковариацию с некоторым разбросом, чтобы убедиться, что мы сравниваем яблоки с яблоками. Это нормализованное число известно как корреляция.

Конечные заметки

Вопросы о корреляции очень часто встречаются в интервью. Главное знать, что корреляция - это оценка линейной зависимости двух переменных. Корреляция является транзитивной для ограниченного диапазона пар корреляций. На него также сильно влияют выбросы. Мы узнали, что ни Корреляция не подразумевает Причинность, ни наоборот.

Удалось ли вам ответить на все вопросы в начале этой статьи? Помогла ли эта статья вам развеять какие-либо сомнения относительно корреляции? Если у вас есть еще вопросы о корреляции, мы будем рады ответить .

Исследование, описанное в статье про Вопросы о корреляции для экзамена и тестов на собеседовании, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Вопросы о корреляции для экзамена и тестов на собеседовании и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.