Выборочная (эмпирическая) функция распределения с примерами кратко

Лекция

Привет, Вы узнаете о том , что такое выборочная функция распределения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое выборочная функция распределения, эмпирическая функция распределения , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Выборочная (эмпирическая) функция распределения в математической статистике — это приближение теоретической функции распределения, построенное с помощью выборки из него.

Определение

Пусть Выборочная (эмпирическая) функция распределения с примерами — выборка объема , порожденная случайной величиной , задаваемой функцией распределения . Будем считать, что Выборочная (эмпирическая) функция распределения с примерами , где , — независимые случайные величины, определенные на некотором пространстве элементарных исходов Выборочная (эмпирическая) функция распределения с примерами . Пуст . Определим функцию следующим образом:

Выборочная (эмпирическая) функция распределения с примерами ,

где Выборочная (эмпирическая) функция распределения с примерами — индикатор события , — функция Хевисайда. Таким образом, значение функции в точке равно относительной частоте элементов выборки, не превосходящих значение Выборочная (эмпирическая) функция распределения с примерами . Функция называется выборочной функцией распределения случайной величины , или эмпирической функцией выборки, и является аппроксимацией для функции Выборочная (эмпирическая) функция распределения с примерами . Существует теорема Колмогорова, утверждающая, что при функция равномерно сходится к , и указывающая скорость сходимости. Для каждого положительного Выборочная (эмпирическая) функция распределения с примерами , — случайная величина со значением .

Поскольку неизвестное распределение Выборочная (эмпирическая) функция распределения с примерами можно описать, например, его функцией распределения 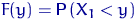, построим по выборке «оценку» для этой функции.

Определение 1.

Эмпирической функцией распределения, построенной по выборке 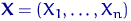Выборочная (эмпирическая) функция распределения с примерами объема 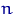, называется случайная функция , при каждом 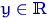равная

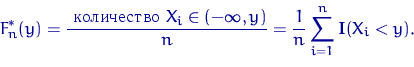
$\begin{displaymath} F^*_n(y)=\dfrac{\textrm{ количество } X_i\in(-\infty,y)}{n} =\frac{1}{n}\sum\limits_{i=1}^n {\mathbf I}(X_i<y).\end{displaymath}$

Напоминание: Случайная функция

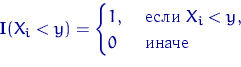
$\begin{displaymath} {\mathbf I}(X_i<y)=\begin{cases} 1, & \textrm{ если } X_i<y, \cr 0 & \textrm{ иначе } \end{cases}\end{displaymath}$

называется индикатором события 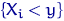Выборочная (эмпирическая) функция распределения с примерами . Об этом говорит сайт https://intellect.icu . При каждом 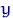это — случайная величина, имеющая распределение Бернулли с параметром Выборочная (эмпирическая) функция распределения с примерами .

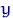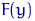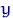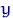Иначе говоря, при любом Выборочная (эмпирическая) функция распределения с примерами значение , равное истинной вероятности случайной величине быть меньше , оценивается долей элементов выборки, меньших Выборочная (эмпирическая) функция распределения с примерами .

Если элементы выборки 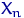Выборочная (эмпирическая) функция распределения с примерами , , упорядочить по возрастанию (на каждом элементарном исходе), получится новый набор случайных величин, называемый вариационным рядом:

$\begin{displaymath} X_{(1)}\leqslant X_{(2)} \leqslant \ldots \leqslant X_{(n-1)}\leqslant X_{(n)}.\end{displaymath}$

Здесь

$\begin{displaymath} X_{(1)}=\min\{X_1, \ldots, X_n\}, \quad X_{(n)}=\max\{X_1, \ldots, X_n\}.\end{displaymath}$

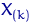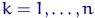Элемент Выборочная (эмпирическая) функция распределения с примерами , , называется -м членом вариационного ряда или -й порядковой статистикой.

Основные свойства

Пусть зафиксирован элементарный исход . Тогда является функцией распределения дискретного распределения, задаваемого следующей функцией вероятности:

Выборочная (эмпирическая) функция распределения с примерами ,

где Выборочная (эмпирическая) функция распределения с примерами , а — количество элементов выборки, равных . В частности, если все элементы выборки различны, то .

Математическое ожидание этого распределения имеет вид:

Выборочная (эмпирическая) функция распределения с примерами .

Таким образом, выборочное среднее — это теоретическое среднее выборочного распределения. Аналогично, выборочная дисперсия — это теоретическая дисперсия выборочного распределения.

Случайная величина имеет биномиальное распределение:

Выборочная (эмпирическая) функция распределения с примерами .

выборочная функция распределения (x)} является несмещенной оценкой функции распределения :

Выборочная (эмпирическая) функция распределения с примерами .

Дисперсия выборочной функции распределения имеет вид:

Выборочная (эмпирическая) функция распределения с примерами .

Согласно усиленному закону больших чисел, выборочная функция распределения сходится почти наверное к теоретической функции распределения:

Выборочная (эмпирическая) функция распределения с примерами почти наверное при .

Выборочная функция распределения является асимптотически нормальной оценкой теоретической функции распределения. Если , то

Выборочная (эмпирическая) функция распределения с примерами по распределению при .

Пример 1.

Выборка: ${\mathbf X}= (0;2;1;2{,}6;3{,}1;4{,}6;1;4{,}6;6;2{,}6;6;7;9;\ 9;2{,}6).$
Вариационный ряд: 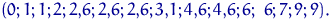$(0;1;1;2;2{,}6;2{,}6;2{,}6;3{,}1;4{,}6;4{,}6;6;\ 6;7;9;9).$

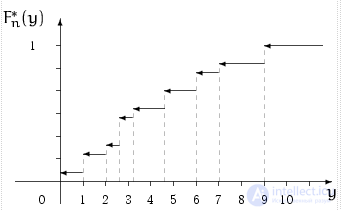
Выборочная (эмпирическая) функция распределения с примерами

Рис 1

эмпирическая функция распределения имеет скачки в точках выборки, величина скачка в точке 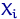Выборочная (эмпирическая) функция распределения с примерами равна 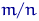, где — количество элементов выборки, совпадающих с .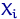

Можно построить эмпирическую функцию распределения по вариационному ряду:

$\begin{displaymath} F_n^*(y)=\begin{cases} 0, & \textrm{ если } y\leqslant X_{(1... ...nt X_{(k+1)}, \cr 1 & \textrm{ при } y\gt X_{(n)}. \end{cases}\end{displaymath}$

Другой характеристикой распределения является таблица (для дискретных распределений) или плотность (для абсолютно непрерывных). Эмпирическим, или выборочным аналогом таблицы или плотности является так называемая гистограмма.

Гистограмма строится по группированным данным. Предполагаемую область значений случайной величины 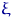Выборочная (эмпирическая) функция распределения с примерами (или область выборочных данных) делят независимо от выборки на некоторое количество интервалов (не обязательно одинаковых). Пусть 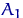Выборочная (эмпирическая) функция распределения с примерами , , — интервалы на прямой, называемые интервалами группировки. Обозначим для 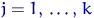через число элементов выборки, попавших в интервал Выборочная (эмпирическая) функция распределения с примерами :

$\begin{equation} \nu_j=\{\textrm{\,число } X_i \in A_j\}=\sum\limits_{i=1}^n {\m... ...A_j), \quad \textrm{ здесь } \quad \sum\limits_{j=1}^k \nu_j = n.\end{equation}$ (1)

На каждом из интервалов Выборочная (эмпирическая) функция распределения с примерами строят прямоугольник, площадь которого пропорциональна . Общая площадь всех прямоугольников должна равняться единице. Пусть Выборочная (эмпирическая) функция распределения с примерами — длина интервала . Высота 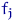прямоугольника над равна

$\begin{displaymath} f_j=\dfrac{\nu_j}{n l_j}.\end{displaymath}$

Полученная фигура называется гистограммой.

Пример 2.

Имеется вариационный ряд (см. пример 1):

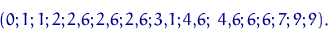
$\begin{displaymath} (0;1;1;2;2{,}6;2{,}6;2{,}6;3{,}1;4{,}6;\ 4{,}6;6;6;7;9;9).\end{displaymath}$

Разобьем отрезок 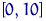Выборочная (эмпирическая) функция распределения с примерами на 4 равных отрезка. В отрезок 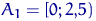попали 4 элемента выборки, в 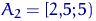— 6, в 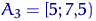— 3, и в отрезок попали 2 элемента выборки. Строим гистограмму (рис. 2). На рис. 3 — тоже гистограмма для той же выборки, но при разбиении области на 5 равных отрезков.

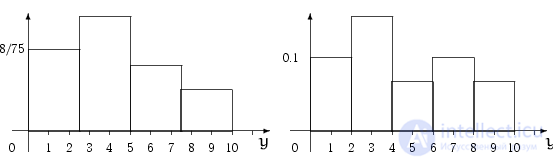
Выборочная (эмпирическая) функция распределения с примерами

рис 2 рис 3

Замечание 1.

В курсе «Эконометрика» утверждается, что наилучшим числом интервалов группировки («формула Стерджесса») является 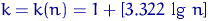Выборочная (эмпирическая) функция распределения с примерами .

Здесь 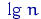Выборочная (эмпирическая) функция распределения с примерами — десятичный логарифм, поэтому 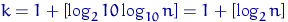, т.е. при увеличении выборки вдвое число интервалов группировки увеличивается на 1. Заметим, что чем больше интервалов группировки, тем лучше. Но, если брать число интервалов, скажем, порядка 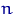Выборочная (эмпирическая) функция распределения с примерами , то с ростом 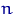гистограмма не будет приближаться к плотности.

Справедливо следующее утверждение:

Если плотность распределения элементов выборки является непрерывной функцией, то при 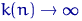Выборочная (эмпирическая) функция распределения с примерами так, что 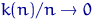, имеет место поточечная сходимость по вероятности гистограммы к плотности.

Так что выбор логарифма разумен, но не является единственно возможным.

Вау!! 😲 Ты еще не читал? Это зря!

ряды распределения , полигон , гистограмма , кумулята ,
Теорема Гливенко — Кантелли
Теорема Колмогорова

Исследование, описанное в статье про выборочная функция распределения, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое выборочная функция распределения, эмпирическая функция распределения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про выборочная функция распределения

Выборочная (эмпирическая) функция распределения с примерами кратко

Определение

Основные свойства

Вау!! 😲 Ты еще не читал? Это зря!

Комментарии

Оставить комментарий

Теория вероятностей. Математическая статистика и Стохастический анализ

Термины: Теория вероятностей. Математическая статистика и Стохастический анализ