Лекция
Привет, Вы узнаете о том , что такое плотность распределения системы двух случайных величин, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое плотность распределения системы двух случайных величин , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Введенная в предыдущем 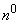 характеристика системы - функция распределения - существует для систем любых случайных величин, как прерывных, так и непрерывных. Основное практическое значение имеют системы непрерывных случайных величин. Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.
характеристика системы - функция распределения - существует для систем любых случайных величин, как прерывных, так и непрерывных. Основное практическое значение имеют системы непрерывных случайных величин. Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.
Вводя в рассмотрение плотность распределения для одной случайной величины, мы определяли ее как предел отношения вероятности попадания на малый участок к длине этого участка при ее неограниченном уменьшении. Аналогично определим плотность распределения системы двух величин.
Пусть имеется система двух непрерывных случайных величин 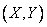 , которая интерпретируется случайной точкой на плоскости
, которая интерпретируется случайной точкой на плоскости 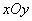 . Рассмотрим на этой плоскости малый прямоугольник
. Рассмотрим на этой плоскости малый прямоугольник 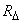 со сторонами
со сторонами 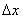 и
и 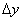 , примыкающий к точке с координатами
, примыкающий к точке с координатами  (рис. 8.3.1). Вероятность попадания в этот прямоугольник по формуле (8.2.2) равна
(рис. 8.3.1). Вероятность попадания в этот прямоугольник по формуле (8.2.2) равна
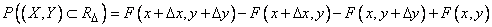
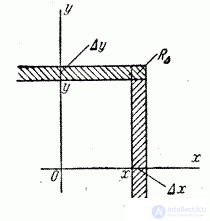
Рис. 8.3.1
Разделим вероятность попадания в прямоугольник 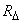 на площадь этого прямоугольника и перейдем к пределу при
на площадь этого прямоугольника и перейдем к пределу при 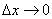 и
и 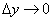 :
:
 (8.3.1)
(8.3.1)
Предположим, что функция 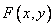 не только непрерывна, но и дифференцируема; тогда правая часть формулы (8.3.1) представляет собой вторую смешанную частную производную функции
не только непрерывна, но и дифференцируема; тогда правая часть формулы (8.3.1) представляет собой вторую смешанную частную производную функции 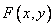 по
по 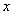 и
и 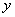 . Обозначим эту производную
. Обозначим эту производную 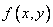 :
:
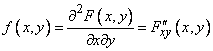 (8.3.2)
(8.3.2)
Функция 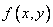 называется плотностью распределения системы.
называется плотностью распределения системы.
Таким образом, плотность распределения системы представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю; она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам.
Если воспользоваться «механической» интерпретацией распределения системы как распределения единичной массы по плоскости  , функция
, функция 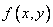 представляет собой плотность распределения массы в точке
представляет собой плотность распределения массы в точке  .
.

Рис. 8.3.2
Геометрически функцию 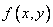 можно изобразить некоторой поверхностью (рис. 8.3.2). Эта поверхность аналогична кривой распределении для одной случайной величины и называется поверхностью распределения.
можно изобразить некоторой поверхностью (рис. 8.3.2). Эта поверхность аналогична кривой распределении для одной случайной величины и называется поверхностью распределения.
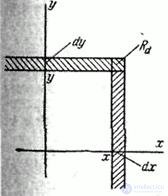
Рис. 8.3.3
Если пересечь поверхность распределения 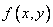 плоскостью, параллельной плоскости
плоскостью, параллельной плоскости 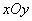 , и спроектировать полученное сечение на плоскость
, и спроектировать полученное сечение на плоскость 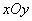 , получится кривая, в каждой точке которой плотность распределения постоянна. Об этом говорит сайт https://intellect.icu . Такие кривые называются кривыми равной плотности. Кривые равной плотности, очевидно, представляют собой горизонтали поверхности распределения. Часто бывает удобно задавать распределение семейством кривых равной плотности.
, получится кривая, в каждой точке которой плотность распределения постоянна. Об этом говорит сайт https://intellect.icu . Такие кривые называются кривыми равной плотности. Кривые равной плотности, очевидно, представляют собой горизонтали поверхности распределения. Часто бывает удобно задавать распределение семейством кривых равной плотности.
Рассматривая плотность распределения 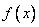 для одной случайной величины, мы ввели понятие «элемента вероятности»
для одной случайной величины, мы ввели понятие «элемента вероятности» 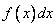 . Это есть вероятность попадания случайной величины
. Это есть вероятность попадания случайной величины 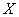 на элементарный участок
на элементарный участок 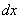 , прилегающий к точке
, прилегающий к точке 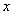 . Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение
. Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение
 .
.
Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами 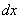 ,
,  , примыкающий к точке
, примыкающий к точке  (рис. 8.3.3).
(рис. 8.3.3).
Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью 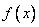 и опирающегося на элементарный прямоугольник
и опирающегося на элементарный прямоугольник 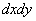 (рис. 8.3.4).
(рис. 8.3.4).
Пользуясь понятием элемента вероятности, выведем выражение для вероятности попадания случайной точки в произвольную область 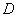 . Эта вероятность, очевидно, может быть получена суммированием (интегрированием) элементов вероятности по всей области
. Эта вероятность, очевидно, может быть получена суммированием (интегрированием) элементов вероятности по всей области 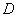 :
:
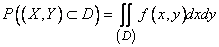 (8.3.3)
(8.3.3)
Геометрически вероятность попадания в область 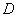 изображается объемом цилиндрического тела
изображается объемом цилиндрического тела 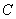 , ограниченного сверху поверхностью распределения и опирающегося на область
, ограниченного сверху поверхностью распределения и опирающегося на область 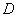 (рис. 8.3.5).
(рис. 8.3.5).

Рис. 8.3.4 Рис. 8.3.5
Из общей формулы (8.3.3) вытекает формула для вероятности попадания в прямоугольник 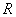 , ограниченный абсциссами
, ограниченный абсциссами 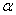 и
и 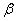 и ординатами
и ординатами 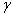 и
и 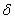 (рис. 8.3.5);
(рис. 8.3.5);
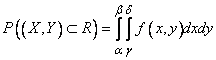 . (8.3.4)
. (8.3.4)
Воспользуемся формулой (8.3.4) для того, чтобы выразить функцию распределения системы 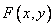 через плотность распределение
через плотность распределение 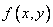 . Функция распределения
. Функция распределения 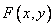 есть вероятность попадания в бесконечный квадрант; последний можно рассматривать как прямоугольник, ограниченный абсциссами -
есть вероятность попадания в бесконечный квадрант; последний можно рассматривать как прямоугольник, ограниченный абсциссами - 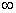 и
и 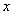 и ординатами -
и ординатами - 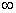 и
и 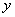 . По формуле (8.3.4) имеем:
. По формуле (8.3.4) имеем:
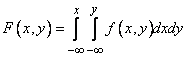 . (8.3.5)
. (8.3.5)
Легко убедиться в следующих свойствах плотности распределения системы:
1. Плотность распределения системы есть функция неотрицательная:
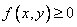 .
.
Это ясно из того, что плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника - и, следовательно, отрицательной быть не может.
2. Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице:
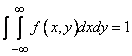 (8.3.6)
(8.3.6)
Это видно из того, что интеграл (8.3.6) есть не что иное, как вероятность попадания во всю плоскость 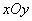 , т.е. вероятность достоверного события.
, т.е. вероятность достоверного события.
Геометрически это свойство означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью 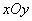 , равен единице.
, равен единице.
Пример 1. Система двух случайных величин 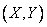 подчинена закону распределения с плотностью
подчинена закону распределения с плотностью
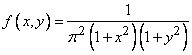 .
.
Найти функцию распределения 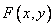 . Определить вероятность попадания случайной точки
. Определить вероятность попадания случайной точки 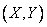 в квадрат
в квадрат 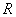 (рис. 8.3.6).
(рис. 8.3.6).
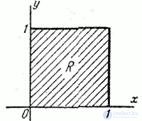
Рис. 8.3.6
Решение. Функцию распределения 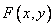 находим по формуле (8.3.5).
находим по формуле (8.3.5).
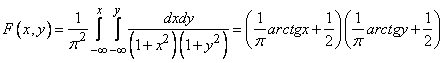 .
.
Вероятность попадания в прямоугольник 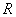 находим по формуле (8.3.4):
находим по формуле (8.3.4):
 .
.
Пример 2. Поверхность распределения системы  представляет собой прямой круговой конус, основанием которого служит круг радиуса
представляет собой прямой круговой конус, основанием которого служит круг радиуса 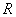 с центром в начале координат. Написать выражение плотности распределения. Определить вероятность того, что случайная точка
с центром в начале координат. Написать выражение плотности распределения. Определить вероятность того, что случайная точка  попадет в круг
попадет в круг 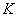 радиуса
радиуса 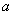 (рис. 8.3.7), причем
(рис. 8.3.7), причем 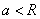 .
.
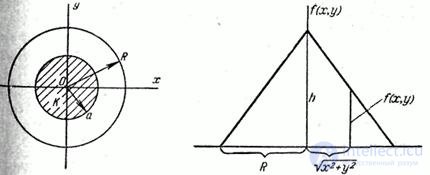
Рис. 8.3.7 Рис. 8.3.8
Решение. Выражение плотности распределения внутри круга 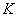 находим из рис. 8.3.8:
находим из рис. 8.3.8:
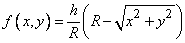 ,
,
где  - высота конуса. Величину
- высота конуса. Величину  определяем так, чтобы объем конуса был равен единице:
определяем так, чтобы объем конуса был равен единице: 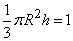 , откуда
, откуда
 ,
,
и
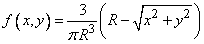 .
.
Вероятность попадания в круг 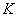 определяем по формуле (8.3.4):
определяем по формуле (8.3.4):
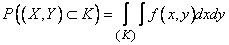 . (8.3.7)
. (8.3.7)
Для вычисления интеграла (8.3.7) удобно перейти к полярной системе координат 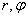 :
:
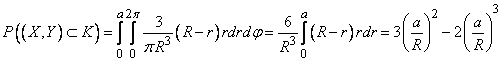 .
.
Информация, изложенная в данной статье про плотность распределения системы двух случайных величин , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое плотность распределения системы двух случайных величин и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про плотность распределения системы двух случайных величин
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ