14.6. Оценки для числовых характеристик системы случайных величин кратко

Привет, Вы узнаете о том , что такое оценки для числовых характеристик системы случайных величин, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое оценки для числовых характеристик системы случайных величин , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В 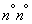 14.1 - 14.4 мы рассмотрели задачи, связанные с оценками для числовых характеристик одной случайной величины при ограниченном числе опытов и построением для этих характеристик доверительных интервалов.

 

Аналогичные вопросы возникают и при обработке ограниченного числа наблюдений над двумя и более случайными величинами.

Здесь мы ограничимся рассмотрением только точечных оценок для характеристик системы.

Рассмотрим сначала случай двух случайных величин.

Имеются результаты 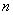 независимых опытов над системой случайных величин 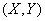, давшие результаты:

; ; …; .

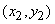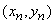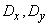Требуется найти оценки для числовых характеристик системы: математических ожиданий , дисперсий  и корреляционного момента .

Этот вопрос решается аналогично тому, как мы решили его для одной случайной величины. Несмещенными оценками для математических ожиданий будут средние арифметические:

; ,                  (14.6.1)

а для элементов корреляционной матрицы -

                     (14.6.2)

Доказательство может быть проведено аналогично 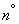 14.2.

При непосредственном вычислении оценок для дисперсий и корреляционного момента часто бывает удобно воспользоваться связью между центральными и начальными статистическими моментами:

                (14.6.3)

где

                      (14.6.4)

Вычислив статистические моменты по формулам (14.6.3), можно затем найти несмещенные оценки для элементов корреляционной матрицы по формулам:

                 (14.6.5)

Пример. Произведены стрельбы с самолета по земле одиночными выстрелами. Зарегистрированы координаты точек попадания и одновременно записаны соответствующие значения угла скольжения самолета. Наблюденные значения угла скольжения  (в тысячных радиана) и абсциссы точки попадания 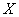 (в метрах) приведены в таблице 14.6.1.

Таблица 14.6.1

1	-8	-10	11	+3	-1
2	+10	-2	12	-2	+4
3	+22	+4	13	+28	+12
4	+55	+10	14	+62	+20
5	+2	-1	15	-10	-11
6	-39	-1+	16	-8	+2
7	-15	-8	17	+22	+14
8	+5	-2	18	+3	+6
9	+10	+6	19	-32	-12
10	+18	+8	20	+8	+1

Найти оценки для числовых характеристик системы .

Решение. Для наглядности наносим все пары значений  на график (рис. 14.6.1). Расположение точек на графике уже свидетельствует о наличии определенной зависимости (положительной корреляции) между  .

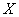По формулам (14.6.1) вычисляем средние значения величин  и 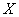 - оценки для математических ожиданий:

; .

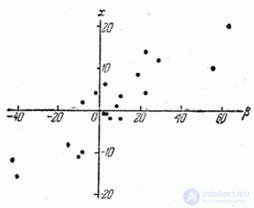
Рис. 14.6.1.

Далее находим статистические вторые начальные моменты:

;

.

По формулам (14.6.3) находим статистические дисперсии:

;

.

Для нахождения несмещенных оценок умножим статистические дисперсии на ; получим:

,

.

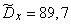Соответственно средние квадратические отклонения равны:

; .

По последней формуле (14.6.4) находим статистический начальным момент:

и статистический корреляционный момент:

.

Для определения несмещенной оценки умножаем его на ; получаем:

,

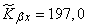откуда оценка для коэффициента корреляции равна:

.

Полученное сравнительно большое значение 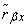 указывает на наличие существенной связи между  и 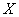; на этом основании можно предполагать, что скольжение является основной причиной боковых отклонений снарядов.

Перейдем к случаю обработки наблюдений над системой произвольного числа случайных величин.

Имеется система 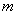 случайных величин

.

Над системой произведено 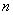 независимых наблюдений; результаты этих наблюдений оформлены в виде таблицы, каждая строка которой содержит  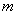значений, принятых случайными величинами  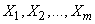в одном наблюдении (табл. 14.6.2).

Таблица 14.6.2

Числа, стоящие в таблице и занумерованные двумя индексами, представляют собой зарегистрированные результаты наблюдений; первый индекс обозначает номер случайной величины, второй - номер наблюдения, так что  - это значение, принятое величиной 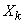 в -м наблюдении.

Требуется найти оценки для числовых характеристик системы: математических ожиданий 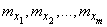 и элементов корреляционной матрицы:

.

По главной диагонали корреляционной матрицы, очевидно, стоят дисперсии случайных величин :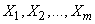

; ; …; .

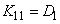Оценки для математических ожиданий найдутся как средние арифметические:

  .                       (14.6.6)

Несмещенные оценки для дисперсий определятся по формулам

,                      (14.6.7)

а для корреляционных моментов - по формулам

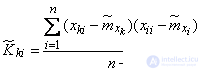.                   (14.6.8)

По этим данным определяются оценки для элементов нормированной корреляционной матрицы:

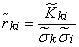,               (14.6.9)

где

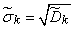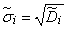;  .                   (14.6.10)

Пример. Об этом говорит сайт https://intellect.icu . Сброшено 10 серий бомб, по 5 бомб в каждой, и зарегистрированы точки попадания. Результаты опытов сведены в таблицу 14.6.3. В таблице буквой  обозначен номер серии;  - номер бомбы в серии.

Требуется определить подходящие значения числовых характеристик - математических ожиданий и элементов корреляционных матриц - для системы пяти случайных величин

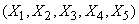
и системы пяти случайных величин

.

Решение. Оценки для математических ожиданий найдутся как средние арифметические по столбцам:

; ; ; ; ;

; ; ; ; .

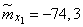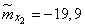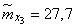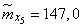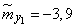При вычислении элементов корреляционной матрицы мы не будем, как в прежних примерах, пользоваться соотношениями между начальными и центральными моментами; в данном случае ввиду сильно изменяющихся математических ожиданий пользование этим приемом не даст преимуществ. Будем вычислять оценки для моментов непосредственно по формулам (14.6.2). Для этого вычтем из каждого элемента таблицы 14.6.3 среднее значение соответствующего столбца. Результаты сведем в таблицу 14.6.4.

Таблица 14.6.3

Абсцисса X						Абсцисса Y
	1	2	3	4	5	1	2	3	4	5
1	-120	-20	2	60	180	-20	-15	-8	-6	-2
2	-108	-75	-20	20	80	40	60	120	125	130
3	-200	-120	-80	-20	10	-25	-30	-20	-10	2
4	-55	-2	40	120	200	-100	-75	-35	2	2
5	5	60	100	165	220	-40	-30	-25	-30	-45
6	-240	-202	-140	-88	-30	80	30	25	10	2
7	10	65	120	160	205	14	25	25	30	10
8	-40	0	65	103	170	80	75	60	10	-4
9	-100	-40	-10	55	105	-70	-60	-30	-10	0
10	105	135	190	280	330	2	4	10	12	4

Таблица 14.6.4

	1	2	3	4	5	1	2	3	4	5
1	-45,7	-0,1	-25,7	-25,8	33,0	-16,1	-13,4	-20,2	-19,3	-11,9
2	-33,	-55,1	-37,7	-65,8	-67,0	43,9	61,6	107,8	111,7	120,1
3	-125,7	-100,1	-107,7	-105,8	-137,0	-21,1	-28,4	-32,2	-23,3	-7,9
4	19,3	17,9	12,3	34,2	53,0	-96,1	-73,4	-47,2	-11,3	-7,9
5	79,3	79,9	72,3	79,2	73,0	-36,1	-28,4	-37,2	-43,3	-54,9
6	-165,7	-182,1	-167,7	-173,8	-177,0	83,9	31,6	12,8	-3,3	-7,9
7	84,3	84,9	92,3	74,2	58,0	17,9	26,6	12,8	16,7	0,1
8	34,3	19,9	37,3	17,2	23,0	83,9	76,6	47,8	-3,3	-13,9
9	-25,7	-20,1	-37,7	-30,8	-42,0	-66,1	-58,4	-42,2	-23,3	-9,9
10	179,3	154,9	162,3	194,2	183,0	5,9	5,6	-2,2	-1,3	-5,9

Возводя эти числа в квадрат, суммируя по столбцам и деля на 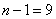, получим оценки для дисперсий и средних квадратических отклонений:

; ; ;

; ;

; ; ; ; .

; ; ;

; ;

; ; ; ; .

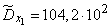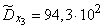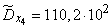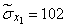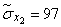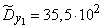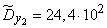Чтобы найти оценку для корреляционного момента, например, между величинам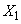и  и 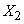 составим столбец попарных произведении чисел, стоящих в первом и втором столбцах таблицы 14.6.4. Сложив все эти произведения и разделив сумму на , получим:

.

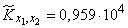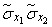Деля  на  получим:

.

Аналогично находим все остальные элементы корреляционных матриц. Для удобства умножим все элементы обеих матриц моментов на . Получим:

.

(Ввиду симметричности матриц они заполнены только наполовину.)

Нормированные корреляционные матрицы имеют вид:

.

Рассматривая эти матрицы, убеждаемся, что величины 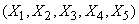 находятся в весьма тесной зависимости, приближающейся к функциональной; величины  связаны менее тесно, и коэффициенты корреляции между ними убывают по мере удаления от главной диагонали корреляционной матрицы.

 

 

Информация, изложенная в данной статье про оценки для числовых характеристик системы случайных величин , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое оценки для числовых характеристик системы случайных величин и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.