1.1. Предмет теории вероятностей

Привет, Вы узнаете о том , что такое предмет теории вероятностей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое предмет теории вероятностей , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Условимся, что мы будем понимать под «случайным явлением».

При научном исследовании различных физических и технических задач часто приходится встречаться с особого типа явлениями, которые принято называть случайными. Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Приведем примеры случайных явлений.

1. Производится стрельба из орудия, установленного под заданным углом к горизонту (рис. 1.1.1).

Пользуясь методами внешней баллистики (науки о движении снаряда в воздухе), можно найти теоретическую траекторию снаряда (кривая  на рис. 1.1.1). Эта траектория вполне определяется условиями стрельбы: начальной скоростью снаряда 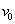, углом бросания  и баллистическим коэффициентом снаряда . Фактическая траектория каждого отдельного снаряда неизбежно несколько отклоняется от теоретической за счет совокупного влияния многих факторов. Среди этих факторов можно, например, назвать: ошибки изготовления снаряда, отклонение веса заряда от номинала, неоднородность структуры заряда, ошибки установки ствола в заданное положение, метеорологические условия и т.д. Если произвести несколько выстрелов при неизменных основных условиях (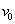,, ), мы получим не одну теоретическую траекторию, а целый пучок или «сноп» траекторий, образующих так называемое «рассеивание снарядов».

Рис. 1.1.1.

2. Одно и то же тело несколько раз взвешивается на аналитических весах; результаты повторных взвешиваний несколько отличаются друг от друга. Эти различия обусловлены влиянием многих второстепенных факторов, сопровождающих операцию взвешивания, таких, как положение тела на чашке весов, случайные вибрации аппаратуры, ошибки отсчета показаний приборов и т.д.

3. Самолет совершает полет на заданной высоте; теоретически он летит горизонтально, равномерно и прямолинейно. Фактически полет сопровождается отклонениями центра массы самолета от теоретической траектории и колебаниям самолета около центра массы. Эти отклонения и колебания являются случайными и связаны с турбулентностью атмосферы; от раза к разу они не повторяются.

4. Производится ряд подрывов осколочного снаряда в определенном положении относительно цели. Результаты отдельных подрывов несколько отличаются друг от друга: меняются общее число осколков, взаимное расположение их траекторий, вес, форма и скорость каждого отдельного осколка. Эти изменения являются случайными и связаны с влиянием таких факторов, как неоднородность металла корпуса снаряда, неоднородность взрывчатого вещества, непостоянство скорости детонации и т.п. В связи с этим различные подрывы, осуществленные, казалось бы, в одинаковых условиях, могут приводить к различным результатам: в одних подрывах цель будет поражена осколками, в других – нет.

Все приведенные примеры рассмотрены здесь под одним и тем же углом зрения: подчеркнуты случайные вариации, неодинаковые результаты ряда опытов, основные условия которых остаются неизменными. Эти вариации всегда связаны с наличием каких-то второстепенных факторов, влияющих на исход опыта, но не заданных в числе его основных условий. Основные условия опыта, определяющие в общих и грубых чертах его протекание, сохраняются неизменными; второстепенные – меняются от опыта к опыту и вносят случайные различия в их результаты.

Совершенно очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали.

Случайные отклонения неизбежно сопутствуют любому закономерному явлению. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления его упрощенную схему, «модель», и предполагая, что в данных условиях опыта явление протекает вполне определенным образом. При этом из бесчисленного множества факторов, влияющих на данное явление, выделяются самые главные, основные, решающие; влиянием остальных, второстепенных факторов просто пренебрегают. Такая схема изучения явлений постоянно применяется в физике, механике, технике. Об этом говорит сайт https://intellect.icu . При пользовании этой схемой для решения любой задачи прежде всего выделяется основной круг  учитываемых условий и выясняется, на какие параметры задачи они влияют; затем применяется тот или иной математический аппарат (например, составляются и интегрируются дифференциальные уравнения, описывающие явление); таким образом выявляется основная закономерность, свойственная данному явлению и дающая возможность предсказать результат опыта по его заданным условиям. По мере развития науки число учитываемых факторов становится все больше; явление исследуется подробнее; научный прогноз становится точнее.

Однако для решения ряда вопросов описанная схема – классическая схема так называемых «точных наук» - оказывается плохо приспособленной. Существуют такие задачи, где интересующий нас исход опыта зависит от столь большого числа факторов, что практически невозможно зарегистрировать и учесть все эти факторы. Это – задачи, в которых многочисленные второстепенные, тесно переплетающиеся между собой случайные факторы играют заметную роль, а вместе с тем число их так велико и влияние столь сложно, что применение классических методов исследования себя не оправдывает.

Рис. 1.1.2.

Рассмотрим пример. Производится стрельба по некоторой цели Ц из орудия, установленного под углом  к горизонту (рис. 1.1.2). Траектории снарядов, как было указано выше, не совпадают между собой; в результате точки падения снарядов на земле рассеиваются. Если размеры цели велики по сравнению с областью рассеивания, то этим рассеиванием, очевидно, можно пренебречь: при правильной установке орудия любой выпущенный снаряд попадает в цель. Если же (как обычно и бывает на практике) область рассеивания снарядов превышает размеры цели, то некоторые из снарядов в связи с влиянием случайных факторов в цель не попадут. Возникает ряд вопросов, например: какой процент выпущенных снарядов в среднем попадает в цель? Сколько нужно потратить снарядов для того, чтобы достаточно надежно поразить цель? Какие следует принять меры для уменьшения расхода снарядов?

Чтобы ответить на подобные вопросы, обычная схема точных наук оказывается недостаточной. Эти вопросы органически связаны со случайной природой явления; для того, чтобы на них ответить, очевидно, нельзя просто пренебречь случайностью, - надо изучить случайное явление рассеивания снарядов с точки зрения закономерностей, присущих ему именно как случайному явлению. Надо исследовать закон, по которому распределяются точки падения снарядов; нужно выяснить случайные причины, вызывающие рассеивание, сравнить их между собой по степени важности и т.д.

Рассмотрим другой пример. Некоторое техническое устройство, например, система автоматического управления, решает определенную задачу в условиях, когда на систему непрерывно воздействуют случайные помехи. Наличие помех приводит к тому, что система решает задачу с некоторой ошибкой, в ряде случаев выходящей за пределы допустимой. Возникают вопросы: как часто будут появляться такие ошибки? Какие следует принять меры для того, чтобы практически исключить их возможность?

Чтобы ответить на такие вопросы, необходимо исследовать природу и структуру случайных возмущений, воздействующих на систему, изучить реакцию системы на такие возмущения, выяснить влияние конструктивных параметров системы на вид этой реакции.

Все подобные задачи, число которых в физике и технике чрезвычайно велико, требуют изучения не только основных, главных закономерностей, определяющих явление в общих чертах, но и анализа случайных возмущений и искажений, связанных с наличием второстепенных факторов и придающих исходу опыта при заданных условиях элемент неопределенности.

Какие же существуют пути и методы для исследования случайных явлений?

С чисто теоретической точки зрения те факторы, которые мы условно назвали «случайными», в принципе ничем не отличаются от других, которые мы выделили в качестве «основных». Теоретически можно неограниченно повышать точность решения каждой задачи, учитывая все новые и новые группы факторов: от самых существенных до самых ничтожных. Однако практически такая попытка одинаково подробно и тщательно проанализировать влияние решительно всех факторов, от которых зависит явление, привела бы только к тому, что решение задачи, в силу непомерной громоздкости и сложности, оказалось бы практически неосуществимым и к тому же не имело бы никакой познавательной ценности.

Например, теоретически можно было бы поставить и решить задачу б определении траектории вполне определенного снаряда, с учетом всех конкретных погрешностей его изготовления, точного веса и конкретной структуры данного, вполне определенного порохового заряда при точно определенных метеорологических данных (температура, давление, влажность, ветер) в каждой точке траектории. Такое решение не только было бы необозримо сложным, но и не имело бы никакой практической ценности, так как относилось бы только к данному конкретному снаряду и заряду в данных конкретных условиях, которые практически больше не повторятся.

Очевидно, должна существовать принципиальная разница в методах учета основных, решающих факторов, определяющих в главных чертах течение явления, и вторичных, второстепенных факторов, влияющих на течение явления в качестве «погрешностей» или «возмущений». Элемент неопределенности, сложности, многопричинности, присущий случайным  явлениям, требует создания специальных методов для изучения этих явлений.

Такие методы и разрабатываются в теории вероятностей. Ее предметом являются специфические закономерности, наблюдаемые в случайных явлениях.

Практика показывает, что, наблюдая в совокупности массы однородных случайных явлений, мы обычно обнаруживаем в них вполне определенные закономерности, своего рода устойчивости, свойственные именно массовым случайным явлениям.

Например, если много раз подряд бросить монету, частота появления герба (отношение числа появившихся гербов к общему числу бросаний) постепенно стабилизируется, приближаясь к вполне определенному числу, именно, к ½. Такое же свойство «устойчивости частот» обнаруживается и при многократном повторении любого другого опыта, исход которого представляется заранее неопределенным, случайным. Так, при увеличении числа выстрелов частота попадания в некоторую цель тоже стабилизируется, приближаясь к некоторому постоянному числу.

Рассмотрим другой пример. В сосуде заключен какой-то объем газа, состоящий из весьма большого числа молекул. Каждая молекула за секунду испытывает множество столкновений с другими молекулами, многократно меняет скорость и направление движения; траектория каждой отдельной молекулы случайна. Известно, что давление газа на стенку сосуда обусловлено совокупностью ударов молекул об эту стенку. Казалось бы, если траектория каждой отдельной молекулы случайна, то и давление на стенку сосуда должно было бы изменяться случайным и неконтролируемым образом; однако это не так. Если число молекул достаточно велико, то давление газа практически не зависит от траекторий отдельных молекул и подчиняется вполне определенной и очень простой закономерности. Случайные особенности, свойственные движению каждой отдельной молекулы, в массе взаимно компенсируются; в результате, несмотря на сложность и запутанность отдельного случайного явления, мы получаем весьма простую закономерность, справедливую для массы случайных явлений. Отметим, что именно массовость случайных явлений обеспечивает выполнение этой закономерности; при ограниченном числе молекул начинают сказываться случайные отклонения от закономерности, так называемые флуктуации.

Рассмотрим еще один пример. По некоторой мишени производится один за другим ряд выстрелов; наблюдается распределение точек попадания на мишени. При ограниченном числе выстрелов точки попадания распределяются по мишени в полном беспорядке, без какой-либо видимой закономерности. По мере увеличения числа выстрелов в расположении точек начинает наблюдаться некоторая закономерность; эта закономерность проявляется тем отчетливее, чем большее количество выстрелов произведено. Расположение точек попадания оказывается приблизительно симметричным относительно некоторой центральной точки: в центральной области группы пробоин они расположены гуще, чем по краям; при этом густота пробоин убывает по вполне определенному закону (так называемый «нормальный закон» или «закон Гаусса», которому будет уделено большое внимание в данном курсе).

Подобные специфические, так называемые «статистические», закономерности наблюдаются всегда, когда мы имеем дело с массой однородных случайных явлений. Закономерности, проявляющиеся в этой массе, оказываются практически независимыми от индивидуальных особенностей отдельных случайных явлений, входящих в массу. Эти отдельные особенности в массе как бы взаимно погашаются, нивелируются, и средний результат массы случайных явлений оказывается практически уже не случайным. Именно эта многократно подтвержденная опытом устойчивость массовых случайных явлений и служит базой для применения вероятностных (статистических) методов исследования. Методы теории вероятностей по природе приспособлены только для исследования массовых случайных явлений; они не дают возможности предсказать исход отдельного случайного явления, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений, предсказать средний исход массы аналогичных опытов, конкретный исход каждого из которых остается неопределенным, случайным.

Чем большее количество однородных случайных явлений участвует в задаче, тем определеннее и отчетливее проявляются присущие им специфические законы, тем с большей уверенностью и точностью можно осуществить научный прогноз.

Во всех случаях, когда применяются вероятностные методы исследования, цель их в том, чтобы, минуя слишком сложное (и зачастую практически невозможное) изучение отдельного явления, обусловленного слишком большим количеством факторов, обратиться непосредственно к законам, управляющим массами случайных явлений. Изучение этих законов позволяет не только осуществлять научный прогноз в своеобразной области случайных явлений, но в ряде случаев помогает целенаправленно влиять на ход случайных явлений, контролировать их, ограничивать сферу действия случайности, сужать ее влияние на практику.

Вероятностный, или статистический, метод в науке не противопоставляет себя классическому, обычному методу точных наук, а является его дополнением, позволяющим глубже анализировать явление с учетом присущих ему элементов случайности.

Характерным для современного этапа развития естественных и технических наук является весьма широкое и плодотворное применение статистических методов во всех областях знания. Это вполне естественно, так как при углубленном изучении любого круга явлений неизбежно наступает этап, когда требуется не только выявление основных закономерностей, но и анализ возможных отклонений от них. В одних науках, в силу специфики предмета и исторических условий, внедрение статистических методов наблюдается раньше, в других – позже. В настоящее время нет почти ни одной естественной науки, в которой, так или иначе, не применялись бы вероятностные методы. Целые разделы современной физики (в частности, ядерная физика) базируются на методах теории вероятностей. Все шире применяются вероятностные методы в современной электротехнике т радиотехнике, метеорологии и астрономии, теории автоматического регулирования и машинной математике.

Обширно поле применения находит теория вероятностей в разнообразных областях военной техники: теория стрельбы и бомбометания, теория боеприпасов, теория прицелов и приборов управления огнем, аэронавигация, тактика и множество других разделов военной науки широко пользуются методами теории вероятностей и ее математическим аппаратом.

Математические законы теории вероятностей – отражение реальных статистических законов, объективно существующих в массовых случайных явлениях природы. К изучению этих явлений теория вероятностей применяет математический метод и по своему методу является одним из разделов математики,  столь же логически точным и строгим, как другие математические науки.

Информация, изложенная в данной статье про предмет теории вероятностей , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое предмет теории вероятностей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.