7.3. Статистический ряд. Гистограмма кратко

Привет, Вы узнаете о том , что такое статистический ряд гистограмма, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое статистический ряд гистограмма , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

При большом числе наблюдений (порядка сотен) простая статистическая совокупность перестает быть удобной формой записи статистического материала - она становится слишком громоздкой и мало наглядной. Для придания ему большей компактности и наглядности статистический материал должен быть подвергнут дополнительной обработке - строится так называемый «статистический ряд».

Предположим, что в нашем распоряжении результаты наблюдений над непрерывной случайной величиной 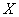, оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюденных значений  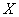на интервалы или «разряды» и подсчитаем количество значений 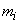, приходящееся на каждый 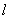-й разряд. Это число разделим на общее число наблюдений  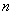и найдем частоту, соответствующую данному разряду:

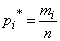.                                                            (7.3.1)

Сумма частот всех разрядов, очевидно, должна быть равна единице.

Построим таблицу, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты. Эта таблица называется статистическим рядом:

Здесь 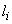 —обозначение 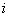-го разряда  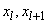- его границы;  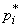- соответствующая частота;  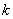- число разрядов.

Пример 1. Об этом говорит сайт https://intellect.icu . Произведено 500 измерений боковой ошибки наводки при стрельбе с самолета по наземной цели. Результаты измерений (в тысячных долях радиана) сведены в статистический ряд:

Здесь 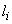 обозначены интервалы значений ошибки наводки;  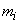- число наблюдений в данном интервале,  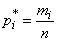- соответствующие частоты.

При группировке наблюденных значений случайной величины по разрядам возникает вопрос о том, к какому разряду отнести значение, находящееся в точности на границе двух разрядов. В этих случаях можно рекомендовать (чисто условно) считать данное значение принадлежащим в равной мере к обоим разрядам и прибавлять к числам 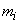, того и другого разряда по .

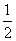Число разрядов, на которые, следует группировать статистический материал, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Практика показывает, что в большинстве случаев рационально выбирать число разрядов порядка 10 – 20. Чем богаче и однороднее статистический материал, тем большее число разрядов можно выбирать при составлении статистического ряда. Длины разрядов могут быть как одинаковыми, так и различными. Проще, разумеется, брать их одинаковыми. Однако при оформлении данных о случайных величинах, распределенных крайне неравномерно, иногда бывает удобно выбирать в области наибольшей плотности распределения разряды более узкие, чем в области малой плотности.

Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь ее равна единице.

В качестве примера можно привести гистограмму для ошибки наводки, построенную по данным статистического ряда, рассмотренного в примере 1 (рис. 7.3.1).

Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины .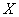

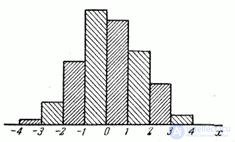
Рис. 7.3.1

Пользуясь данными статистического ряда, можно приближенно построить и статистическую функцию распределения величины 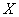. Построение точной статистической функции распределения с несколькими сотнями скачков во всех наблюденных значениях  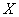слишком трудоемко и себя не оправдывает. Для практики обычно достаточно построить статистическую функцию распределения по нескольким точкам. В качестве этих точек удобно взять границы  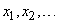разрядов, которые фигурируют в статистическом ряде. Тогда, очевидно,

                    (7.3.2)

Соединяя полученные точки ломанной линией или плавной кривой, получим приближенный график статистической функции распределения.

Пример 2. Построить приближенно статистическую функцию распределения ошибки наводки по данным статистического ряда примера 1.

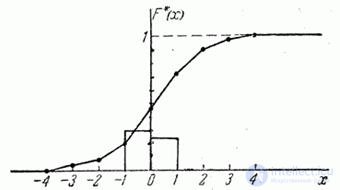
Рис. 7.3.2

Решение. Применяя формулы (7.3.2), имеем:

Приближенный график статистической функции распределения дан на рис. 7.3.2.

Информация, изложенная в данной статье про статистический ряд гистограмма , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое статистический ряд гистограмма и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ