Лекция
Привет, Вы узнаете о том , что такое характеристики положения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое характеристики положения, математическое ожидание, мода, медиана, квантиль, размах , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Среди числовых характеристик случайных величин нужно, прежде всего, отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.
Среднее значение случайной величины есть некоторое число, являющееся как бы ее «представителем» и заменяющее ее при грубо ориентировочных расчетах. Когда мы говорим: «среднее время работы лампы равно 100 часам» или «средняя точка попадания смещена относительно цели на 2 м вправо», мы этим указываем определенную числовую характеристику случайной величины, описывающую ее местоположение на числовой оси, т.е. «характеристику положения».
Из характеристик положения в теории вероятностей важнейшую роль играет математическое ожидание случайной величины, которое иногда называют просто средним значением случайной величины.
• Если ко всем элементам прибавить одно и то же число, то и к среднему арифметическому будет прибавлено то же число

• Если все элементы умножить (разделить) на одно и то же число, то среднее арифметическое умножится (разделится) на то же число
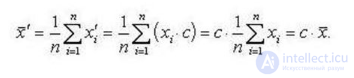
• Сумма отклонений элементов от их среднего арифметического равна нулю

Рассмотрим дискретную случайную величину  , имеющую возможные значения
, имеющую возможные значения  с вероятностями
с вероятностями  . Нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели естественно воспользоваться так называемым «средним взвешенным» из значений
. Нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели естественно воспользоваться так называемым «средним взвешенным» из значений 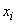 , причем каждое значение
, причем каждое значение 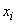 при осреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Таким образом, мы вычислим среднее случайной величины
при осреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Таким образом, мы вычислим среднее случайной величины  , которое мы обозначим
, которое мы обозначим 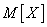 :
:
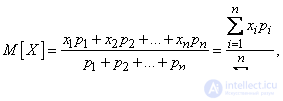
или, учитывая, что 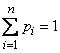 ,
,
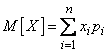 . (5.6.1)
. (5.6.1)
Это среднее взвешенное значение и называется математическим ожиданием случайной величины. Таким образом, мы ввели в рассмотрении одно из важнейших понятий теории вероятностей – понятие математического ожидания.
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Заметим, что в вышеприведенной формулировке определение математического ожидания справедливо, строго говоря, только для дискретных случайных величин; ниже будет дано обобщение этого понятия на случай непрерывных величин.
Для того, чтобы сделать понятие математического ожидания более наглядным, обратимся к механической интерпретации распределения дискретной случайной величины. Пусть на оси абсцисс расположены точки с абсциссами  , в которых сосредоточены соответственно массы
, в которых сосредоточены соответственно массы  , причем
, причем 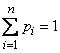 . Тогда, очевидно, математическое ожидание
. Тогда, очевидно, математическое ожидание 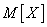 , определяемое формулой (5.6.1), есть не что иное, как абсцисса центра тяжести данной системы материальных точек.
, определяемое формулой (5.6.1), есть не что иное, как абсцисса центра тяжести данной системы материальных точек.
Математическое ожидание случайной величины  связано своеобразной зависимостью со средним арифметическим наблюденных значений случайной величины при большом числе опытов. Эта зависимость того же типа, как зависимость между частотой и вероятностью, а именно: при большом числе опытов среднее арифметическое наблюденных значений случайной величины приближается (сходится по вероятности) к ее математическому ожиданию. Из наличия связи между частотой и вероятностью можно вывести как следствие наличие подобной же связи между средним арифметическим и математическим ожидание.
связано своеобразной зависимостью со средним арифметическим наблюденных значений случайной величины при большом числе опытов. Эта зависимость того же типа, как зависимость между частотой и вероятностью, а именно: при большом числе опытов среднее арифметическое наблюденных значений случайной величины приближается (сходится по вероятности) к ее математическому ожиданию. Из наличия связи между частотой и вероятностью можно вывести как следствие наличие подобной же связи между средним арифметическим и математическим ожидание.
Действительно, рассмотрим дискретную случайную величину  , характеризуемую рядом распределения:
, характеризуемую рядом распределения:

где  .
.
Пусть производится  независимых опытов, в каждом из которых величина
независимых опытов, в каждом из которых величина  принимает определенное значение. Предположим, что значение
принимает определенное значение. Предположим, что значение 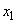 появилось
появилось 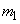 раз, значение
раз, значение 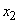 появилось
появилось 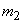 раз, вообще значение
раз, вообще значение 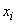 появилось
появилось  раз. Очевидно,
раз. Очевидно,
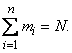
Вычислим среднее арифметическое наблюденных значений величины  , которое, в отличие от математического ожидания
, которое, в отличие от математического ожидания 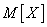 мы обозначим
мы обозначим 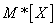 :
:

Но 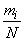 есть не что иное, как частота (или статистическая вероятность) события
есть не что иное, как частота (или статистическая вероятность) события  ; эту частоту можно обозначить
; эту частоту можно обозначить  . Тогда
. Тогда
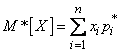 ,
,
т.е. среднее арифметическое наблюденных значений случайной величины равно сумме произведений всех возможных значений случайной величины на частоты этих значений.
При увеличении числа опытов  частоты
частоты  будут приближаться (сходиться по вероятности) к соответствующим вероятностям
будут приближаться (сходиться по вероятности) к соответствующим вероятностям 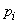 . Следовательно, и среднее арифметическое наблюденных значений случайной величины
. Следовательно, и среднее арифметическое наблюденных значений случайной величины 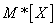 при увеличении числа опытов будет приближаться (сходится по вероятности) к ее математическому ожиданию
при увеличении числа опытов будет приближаться (сходится по вероятности) к ее математическому ожиданию 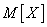 .
.
Сформулированная выше связь между средним арифметическим и математическим ожиданием составляет содержание одной из форм закона больших чисел. Строгое доказательство этого закона будет дано нами в главе 13.
Мы уже знаем, что все формы закона больших чисел констатируют факт устойчивости некоторых средних при большом числе опытов. Здесь речь идет об устойчивости среднего арифметического из ряда наблюдений одной и той же величины. При небольшом числе опытов среднее арифметическое их результатов случайно; при достаточном увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь, приближается к постоянной величине – математическому ожиданию.
Свойство устойчивости средних при большом числе опытов легко проверить экспериментально. Например, взвешивая какое-либо тело в лаборатории на точных весах, мы в результате взвешивания получаем каждый раз новое значение; чтобы уменьшить ошибку наблюдения, мы взвешиваем тело несколько раз и пользуемся средним арифметическим полученных значений. Об этом говорит сайт https://intellect.icu . Легко убедиться, что при дальнейшем увеличении числа опытов (взвешиваний) среднее арифметическое реагирует на это увеличение все меньше и меньше и при достаточно большом числе опытов практически перестает меняться.
Формула (5.6.1) для математического ожидания соответствует случаю дискретной случайной величины. Для непрерывной величины  математическое ожидание, естественно, выражается уже не суммой, а интегралом:
математическое ожидание, естественно, выражается уже не суммой, а интегралом:
 , (5.6.2)
, (5.6.2)
где 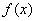 - плотность распределения величины
- плотность распределения величины  .
.
Формула (5.6.2) получается из формулы (5.6.1), если в ней заменить отдельные значения 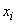 непрерывно изменяющимся параметром х, соответствующие вероятности
непрерывно изменяющимся параметром х, соответствующие вероятности 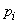 - элементом вероятности
- элементом вероятности  , конечную сумму – интегралом. В дальнейшем мы часто будем пользоваться таким способом распространения формул, выведенных для прерывных величин, на случай непрерывных величин.
, конечную сумму – интегралом. В дальнейшем мы часто будем пользоваться таким способом распространения формул, выведенных для прерывных величин, на случай непрерывных величин.
В механической интерпретации математическое ожидание непрерывной случайной величины сохраняет тот же смысл – абсцисса центра тяжести в случае, когда масса распределена по оси абсцисс непрерывно, с плотностью 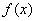 . Эта интерпретация часто позволяет найти математическое ожидание без вычисления интеграла (5.6.2), из простых механических соображений.
. Эта интерпретация часто позволяет найти математическое ожидание без вычисления интеграла (5.6.2), из простых механических соображений.
Выше мы ввели обозначение 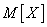 для математического ожидания величины
для математического ожидания величины  . В ряде случаев, когда величина
. В ряде случаев, когда величина 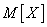 входит в формулы как определенное число, ее удобнее обозначать одной буквой. В этих случаях мы будем обозначать математическое ожидание величины
входит в формулы как определенное число, ее удобнее обозначать одной буквой. В этих случаях мы будем обозначать математическое ожидание величины  через
через 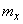 :
:
 .
.
Обозначения 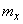 и
и 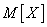 для математического ожидания будут в дальнейшем применяться параллельно в зависимости от удобства той или иной записи формул. Условимся также в случае надобности сокращать слова «математическое ожидание» буквами м.о.
для математического ожидания будут в дальнейшем применяться параллельно в зависимости от удобства той или иной записи формул. Условимся также в случае надобности сокращать слова «математическое ожидание» буквами м.о.
Следует заметить, что важнейшая характеристика положения – математическое ожидание – существует не для всех случайных величин. Можно составить примеры таких случайных величин, для которых математического ожидания не существует, так как соответствующая сумма или интеграл расходятся.
Рассмотрим, например, прерывную случайную величину  с рядом распределения:
с рядом распределения:

Нетрудно убедится в том, что 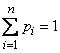 , т.е. ряд распределения имеет смысл; однако сумма
, т.е. ряд распределения имеет смысл; однако сумма 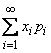 в данном случае расходится и, следовательно, математического ожидания величины
в данном случае расходится и, следовательно, математического ожидания величины  не существует. Однако для практики такие случаи существенного интереса не представляют. Обычно случайные величины, с которыми мы имеем дело, имеют ограниченную область возможных значений и, безусловно, обладают математическим ожиданием.
не существует. Однако для практики такие случаи существенного интереса не представляют. Обычно случайные величины, с которыми мы имеем дело, имеют ограниченную область возможных значений и, безусловно, обладают математическим ожиданием.
Выше мы дали формулы (5.6.1) и (5.6.2), выражающие математическое ожидание соответственно для прерывной и непрерывной случайной величины  .
.
Если величина  принадлежит к величинам смешанного типа, то ее математическое ожидание выражается формулой вида:
принадлежит к величинам смешанного типа, то ее математическое ожидание выражается формулой вида:
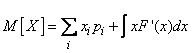 , (5.6.3)
, (5.6.3)
где сумма распространяется на все точки 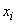 , в которых функция распределения терпит разрыв, а интеграл – на все участки, на которых функция распределения непрерывна.
, в которых функция распределения терпит разрыв, а интеграл – на все участки, на которых функция распределения непрерывна.
Кроме важнейшей из характеристик положения – математического ожидания, - на практике иногда применяются и другие характеристики положения , в частности, мода и медиана случайной величины.
Модой случайной величины называется ее наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. Условимся обозначать моду буквой M. На рис. 5.6.1 и 5.6.2 показана мода соответственно для прерывной и непрерывной случайных величин.
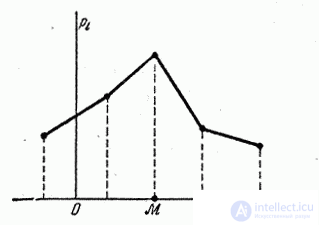
Рис. 5.6.1

Рис. 5.6.2.
Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называется «полимодальным» (рис. 5.6.3 и 5.6.4).
Рис. 5.6.3.
Рис. 5.6.4.
Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом (рис. 5.6.5 и 5.6.6). Такие распределения называют «антимодальными». Примером антимодального распределения может служить распределение, полученное в примере 5, n° 5.1.

Рис. 5.6.5.

Рис. 5.6.6.
В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, когда распределение является симметричным и модальным (т.е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения.

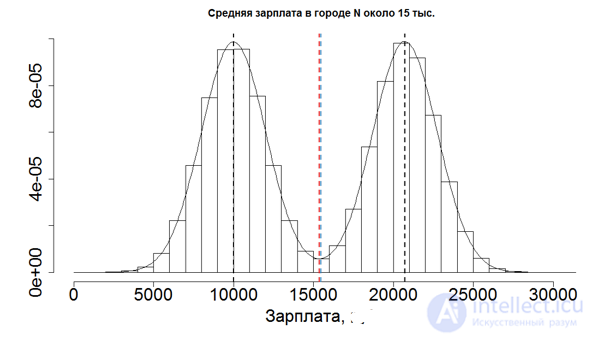
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
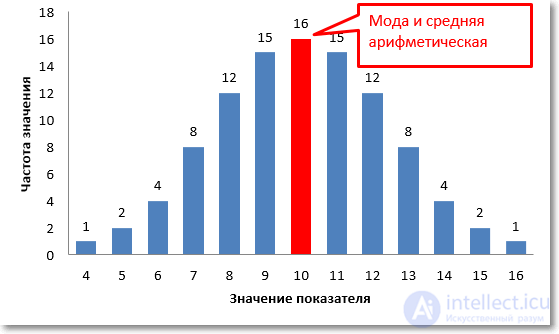
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.

На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
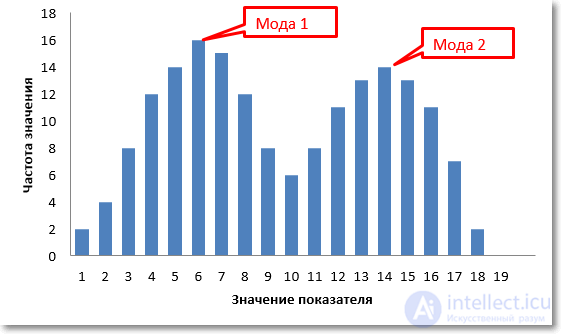
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
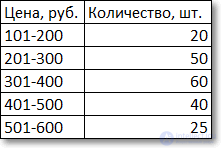
Для наглядности изобразим соответствующую диаграмму.
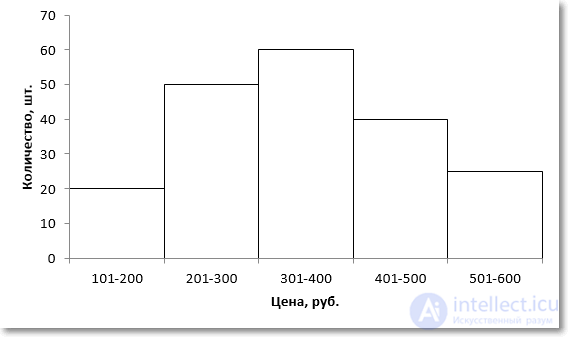
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.

На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.

Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
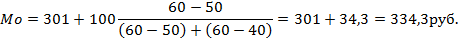
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.

МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно ее определить и для прерывной величины.
Медиана- Средняя точка распределения. Половина наблюдений больше, а половина меньше медианы
Как вычислить медиану дискретной случайной величины:
• Проранжировать наблюдения от меньшего к большему
• Если n нечетное, то медиана – центральный элемент вранжированном списке
• Если n четное, то среднее арифметическое двух центральных элементов

Медианой случайной величины называется такое ее значение 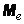 , для которого
, для которого
 ,
,
т.е. одинаково вероятно, окажется ли случайная величина меньше или больше 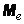 . Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 5.6.7).
. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 5.6.7).
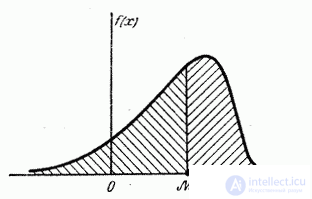
Рис. 5.6.7.
В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
• размах – разница между наибольшим и наименьшим значениями. Недостаток – не характеризует распределение целиком, а только крайние значения
• Среднее абсолютное отклонение:

• Дисперсия и стандартное отклонение

Дисперсия (s2, σ2) – средний квадрат отклонений от среднего арифметического.
Стандартное отклонение (СО) – это корень из дисперсии
Дисперсия и СО по выборке оценивается с учетом степеней свободы (n-1). Только тогда они являются несмещенными оценками σ2 и σ генеральной совокупности
Дисперсия и стандартное отклонение используют только вместе со средним (не с медианой!!!)
• Межквартильный интервал (IQR – interquartile range)
• Медианное абсолютное отклонение (MAD)
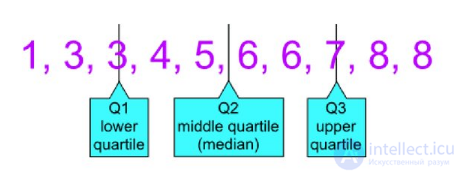
• Нижний (первый) квартиль Q1 – это медиана левой от медианы группы значений в упорядоченном списке. 25% значений меньше Q1
• Верхний (третий) квартиль Q3 – это медиана правой от медианы группы значений. 25% значений больше Q3
• Второй квартиль Q2 – он же медиана
• Межквартильный интервал – одна из мер разброса
• Вычисляется как разница третьего и первого квартилей Q3-Q1
• 1.5IQR – правило нахождения выбивающихся значений
• Если значение находится на расстоянии более 1.5IQR над Q3 или ниже Q1, то это потенциальный выброс
• Five-number summary – непараметрическая форма представления центральной тенденции и разброса распределения:
Минимум – Q1 – Медиана – Q3 – Максимум
• Диаграмма для представления five-number summary
• В классическом виде коробочка это квартили, а усики – это размах
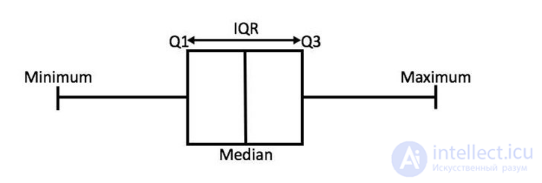
•В модифицированном виде усики – это 1.5IQR, точки – выбивающиеся значения, а доверительный вырез или алмаз – примерный доверительный интервал для медианы, рассчитываемый как 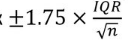
•Считается, что если вырезы (алмазы) не пересекаются, то имеются значимые различия

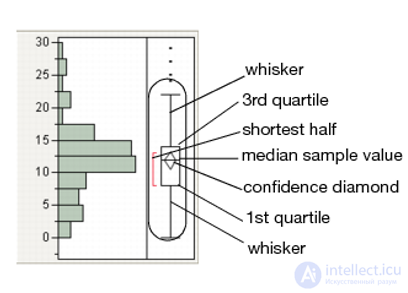
•Медиана модулей отклонений от медианы 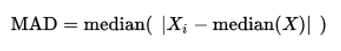
•Часто умножают на коэффициент 1.4826 . В таком случае представляет собой оценку стандартного отклонения σ, как-будто распределение является нормальным
•Различные меры центральной тенденции и разброса характеризуются различной устойчивостью к единичным выбивающимся значениям
•Среднее и особенно дисперсия (стандартное отклонение) являются чувствительными мерами
•Медиана, IQR и MAD характеризуются гораздо меньшей чувствительностью
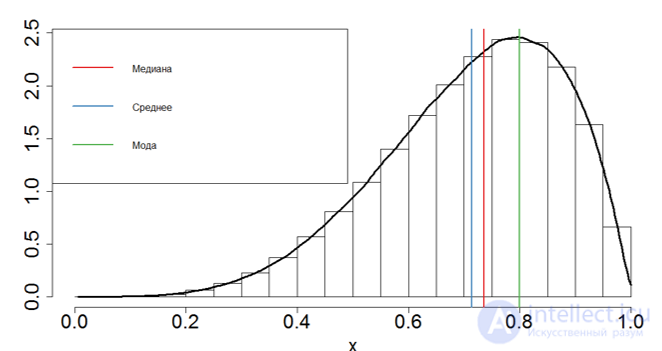

•Средняя зарплата 27.2 тысяч тугриков (s: ± 23 тыс.)
•Медианная зарплата 20.2 тысяч тугриков(MAD: ± 2.25 тыс.)
•Реальный левый пик: 20 ± 2 тыс.
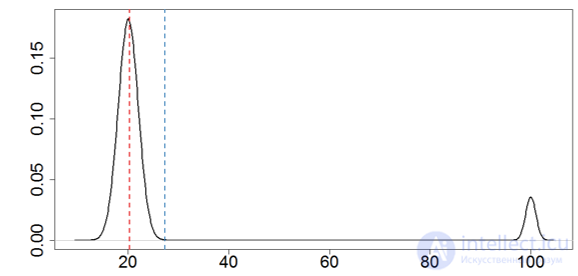
Внимание к модальности! •Среднее и медиана равны
Размах — разность между наибольшим и наименьшим значениями результатов наблюдений. Пусть — взаимно независимые случайные величины с функцией распределения
и плотностью вероятности
. В этом случае размах
определяется как разность между наибольшим и наименьшим значениями среди
; размах
представляет собой случайную величину, которой соответствует функция распределения:
(при w >= 0; если w < 0, то P {W <= w} = 0).
В математической статистике размах, надлежащим образом нормированный, применяется как оценка неизвестного квадратичного отклонения. Например, если имеют нормальное распределение с параметрами (а, s), то при n = 5 и 10, соответственно, величины 0,4299W5 и 0,3249W10 будут несмещенными оценками s. Такие оценки часто используют при статистическом контроле качества, поскольку определение Р. нескольких результатов измерений не требует сложных вычислений.
Информация, изложенная в данной статье про характеристики положения , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое характеристики положения, математическое ожидание, мода, медиана, квантиль, размах и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ