Формула (теорема) Байеса и примеры решения задач кратко

Привет, сегодня поговорим про формула байеса, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое формула байеса, теорема байеса , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

теорема байеса (или формула байеса ) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, взяв в расчет как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятностей, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для ее практического применения требуется большое количество расчетов, вычислений, поэтому байесовские оценки стали активно использовать только после революции в компьютерных и сетевых технологиях.

При возникновении теоремы Байеса вероятности, используемые в теореме, подвергались целому ряду вероятностных интерпретаций. В одной из таких интерпретаций говорилось, что вывод формулы напрямую связан с применением особого подхода к статистическому анализу. Если использовать байесовскую интерпретацию вероятности, то теорема показывает, как личный уровень доверия может кардинально измениться вследствие количества наступивших событий. В этом заключаются выводы Байеса, которые стали основополагающими для байесовской статистики. Однако теорема не только используется в байесовском анализе, но и активно применяется для большого ряда других расчетов.

Психологические эксперименты показали, что люди часто неверно оценивают реальную (математически верную) вероятность события, основываясь на некоем полученном опыте (апостериорная вероятность), поскольку игнорируют саму вероятность предположения (априорная вероятность). Поэтому правильный результат по формуле Байеса может сильно отличаться от интуитивно ожидаемого.

Теорема Байеса названа в честь ее автора Томаса Байеса (1702—1761) — английского математика и священника, который первым предложил использование теоремы для корректировки убеждений, основываясь на обновленных данных. Его работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году , через 2 года после смерти автора. До того, как посмертная работа Байеса была принята и прочитана в Королевском обществе, она была значительно отредактирована и обновлена Ричардом Прайсом. Однако эти идеи не предавались публичной огласке до тех пор, пока не были вновь открыты и развиты Лапласом, впервые опубликовавшим современную формулировку теоремы в своей книге 1812 года «Аналитическая теория вероятностей».

Сэр Гарольд Джеффрис писал, что теорема Байеса «для теории вероятности, то же, что теорема Пифагора для геометрии»^[3

Пусть событие B происходит одновременно с одним из n несовместных событий A1, A2, A3, ... An. Требуется найти вероятность события Ai, если известно, что событие B произошло.

На основании теоремы о вероятности произведения двух событий можно написать

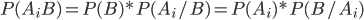
Откуда

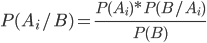
или

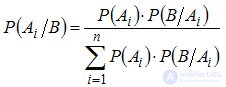(3.2)

Формула (3.2) носит название формулы Байеса.

Формулировка Байесовская вероятность

Формула Байеса: , где — априорная вероятность гипотезы A (смысл такой терминологии см. Об этом говорит сайт https://intellect.icu . ниже); — вероятность гипотезы A при наступлении события B (апостериорная вероятность); — вероятность наступления события B при истинности гипотезы A; — полная вероятность наступления события B.

Доказательство

Формула Байеса вытекает из определения условной вероятности. Вероятность совместного события двояко выражается через условные вероятности

Следовательно

Вычисление P(B)

В задачах и статистических приложениях обычно вычисляется по формуле полной вероятности события, зависящего от нескольких несовместных гипотез, имеющих суммарную вероятность 1.

,

где вероятности под знаком суммы известны или допускают экспериментальную оценку.

В этом случае формула Байеса записывается так:

«Физический смысл» и терминология

Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.

События, отражающие действие «причин», в данном случае называют гипотезами, так как они — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии).

Интерпретация Байеса

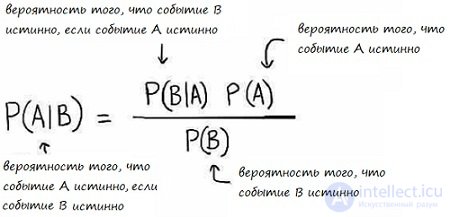
В интерпретации Байеса вероятность измеряет уровень доверия. Теорема Байеса связывает воедино доверие предположению до и после принятия во внимание очевидных доказательств. Например, кто-то предположил, что при подкидывании монетки она будет приземляться в 2 раза чаще решкой вверх, а орлом вниз. Первоначально степень доверия, что такое событие случится, монета упадет именно так — 50 %. Уровень доверия может увеличиться до 70 %, если предположение будет подтверждено доказательством.^{[прояснить]}

Для предположения (гипотезы) A и доказательства B

• P(A) — априорная вероятность гипотезы A, первоначальный уровень доверия предположению A;
• P(A | B) — апостериорная вероятность гипотезы A при наступлении события B;
• отношение P(B | A)/P(B) показывает, как событие B помогает изменить уровень доверия предположению A.

Частотная интерпретация

В частотной интерпретации теорема Байеса исчисляет доли определенных результатов события. Предположим, что некий эксперимент проводился много раз и в некоторых случаях приводил к результатам А и/или B. Тогда:

• P(A) — доля случаев, когда эксперимент привел к результату A.
• P(B) — доля случаев, когда эксперимент привел к результату B.
• P(B | A) — доля случаев с результатом B среди случаев с результатом А.
• P(A | B) — доля случаев с результатом A среди случаев с результатом B.

Роль теоремы Байеса лучше всего можно понять из древовидных диаграмм, представленных справа. Диаграммы демонстрируют различный порядок распределения событий по наличию или отсутствию результатов A и B. Теорема Байеса выступает как связующее звено этих распределений.

Примеры

Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.

Решение. Пусть 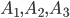— события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут

,,

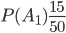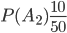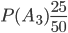
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета

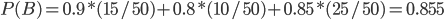
По формуле Байеса находим исходную вероятность

.

Пример 2

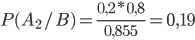Пусть событие — машина не заводится, а гипотеза — в баке нет топлива. Очевидно, что вероятность того, что машина не заведется, если в баке нет топлива, равняется единице. Как следствие, апостериорная вероятность, что в баке нет топлива, если машина не заводится, то есть , равна , то есть отношению априорной вероятности, что в баке нет топлива, к вероятности, что машина не заводится. Например, если априорная вероятность, что в баке нет топлива, равна 0,01, а вероятность, что машина не заводится, равна 0,02 , и случайно выбранная машина не завелась, то вероятность, что в ее баке нет топлива, равна 0,5 (1/2).

Вау!! 😲 Ты еще не читал? Это зря!

Надеюсь, эта статья про формула байеса, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое формула байеса, теорема байеса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про формула байеса