Лекция
закон бенфорда , также известный как закон первых цифр ( Закон Ньюкомба-Бенфорда (НБЛ),), является статистическим законом, который описывает распределение первых цифр (1-9) в наборе чисел, встречающихся в различных реальных данных. Этот закон утверждает, что в большинстве наборов данных первые цифры имеют тенденцию распределяться не равномерно, а по определенному логарифмическому закону.
Согласно закону Бенфорда, в наборах данных, описывающих различные явления, такие как финансовые данные, научные константы, население городов, длины рек и т.д., вероятность того, что первая цифра будет 1, составляет около 30%, в то время как вероятность того, что первая цифра будет 9, всего около 5%.
акон верен для многих таких распределений, но не для всех. Также делает ряд предсказаний частоты встречаемости второй и третьей цифры.
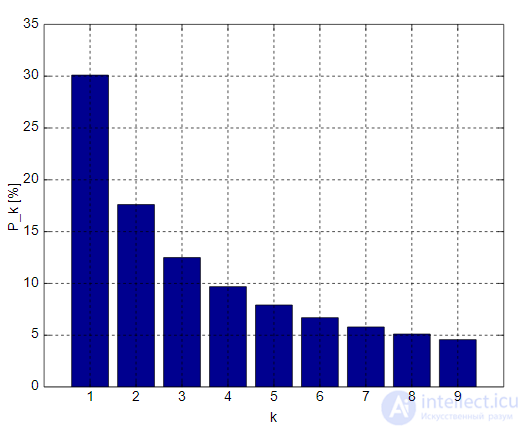
Распределение Бенфорда. По горизонтали — первые значащие цифры, по вертикали — вероятность их появления
Закон, обнаруженный Фрэнком Бенфордом, выглядит так: если у нас основание системы счисления b (b > 2), то для цифры d (d ∈ {1, …, b − 1}) вероятность быть первой значащей цифрой составляет
Это в точности расстояние между d и d+1 на логарифмической шкале с основанием b.
Для равномерного распределения, если вы имеете цифры 1, 2, 3, 4 ,5 ,6 ,7, 8, 9, 0 (=10), то у вас есть 10 отрезков (от 0 до 1,…, от 8 до 9, от 9 до 10). Обратите внимание, все отрезки лежат в диапазоне [0, 10]. Для отрезка [d, d+1] равномерное распределение должно быть пропорционально его длине, то есть длине отрезка [d, d+1], то есть (d+1)-d, поделенное на длину отрезка [0, 10], которая равна 10.
.
Если логарифмы непрерывно распределены, вы должны взять логарифм числа перед тем, как рассмотреть отрезки. Для логарифмов рассматриваем отрезки от 1 до 10 (так как log100 не имеет смысла). В этом случае вы будете иметь интервалы от log101 до log102,…, от log108 до log109, от log109 до log1010. Все отрезки лежат в интервале [log101, log1010]=[0, 1]. Длина последнего равна 1. Итак, рассматриваем отрезок [d, d+1] на обычной шкале, в логарифмической шкале равномерное распределение будет пропорционально его длине, то есть:
.
В таблице ниже представлены найденные Бенфордом значения вероятностей первой цифры для десятичной системы счисления.
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p | 30,1 % | 17,6 % | 12,5 % | 9,7 % | 7,9 % | 6,7 % | 5,8 % | 5,1 % | 4,6 % |
При этом распределение зависит только от системы счисления, но не от единицы измерения. Другими словами, если тонны перевести в фунты, а квадратные километры — в акры, распределение не изменится.
Впервые проявление этого закона заметил американский астроном Саймон Ньюком в 1881 году. Он обнаружил, что книги, содержащие логарифмические таблицы, истрепаны там, где содержатся логарифмы чисел, начинающихся с единицы, и целы для чисел, начинающихся на 9.
Это явление было повторно обнаружено физиком Фрэнком Бенфордом в 1938 году. Бенфорд проанализировал около 20 таблиц, среди которых были данные о площади бассейна 335 рек, удельной теплоемкости и молекулярном весе тысяч химических соединений и, в том числе, номера домов первых 342 улиц, указанных в справочнике. Анализ чисел показал, что единица является первой значащей цифрой с вероятностью не 1/9, как следовало ожидать, а около 1/3.
Впоследствии закон Бенфорда получил свое объяснение — он применим ко множествам чисел, которые могут расти экспоненциально (другими словами, темп роста величины пропорционален ее текущему значению, ). Например, в их число входят счета за электричество, остатки товаров на складах, цены на акции, численность населения, смертность, длины рек, площади стран, высоты самых высоких сооружений в мире.

Сопоставление распределения Бенфорда (красный цвет) и распределения первых букв в словах русского языка (синий цвет). По горизонтали — первые значащие буквы, по вертикали — вероятность их появления.
Закон обычно не действует для распределений с заданными минимальными или максимальными значениями (список компаний с доходом от 50000 до 100000 долларов). Также не подходят распределения, охватывающие только один или два порядка величин (IQ взрослых). Закон Бенфорда не применим ко множеству букв (рис.). Объем данных должен быть достаточен для применения статистических методов.
Закон Бенфорда может быть объяснен разными путями.
Точная форма Закона Бенфорда может быть объяснена если предположить, что равномерно распределены логарифмы чисел; к примеру, вероятность нахождения числа между 100 и 1000 (логарифм между 2 и 3) является такой же, как и между 10 000 и 100 000 (логарифм между 4 и 5). Для многих множеств чисел, особенно имеющих экспоненциальный рост, таких как доходы или цены на бирже, это разумное предположение.
К примеру, если количество увеличивается непрерывно и удваивается каждый год, тогда оно будет в два раза больше начального значения через год, в четыре раза больше начального значения через два года, в восемь раз больше начального значения через три года, и т. д. Когда это количество достигает значения 100, оно будет иметь значащую цифру 1 на протяжении года, достигая 200 в конце первого года. В течение следующего года значение возрастет с 200 до 400; значащая цифра будет 2 (значение будет от 200 до 300) для немногим более семи месяцев (напоминаю, мы имеем дело с экспоненциальным ростом, то есть с 200 до 300 функция растет «медленнее», чем с 300 до 400) и 3 для оставшихся пяти месяцев. На третий год значащая цифра пройдет значения 4, 5, 6, и 7 проводя все меньше времени, чтобы достичь следующей цифры, достигая 800 к концу того года. В начале четвертого года, значащая цифра пройдет от 8 до 9. Значащая цифра станет опять 1, когда значение достигнет 1000 и все начнется сначала, понадобится год, чтобы удвоить значение от 1000 до 2000. Этот пример демонстрирует, что таблицы данных, которые включают измерения экспоненциально растущих величин, будут согласовываться с законом Бенфорда. Однако этот закон выполняется также для многих случаев, когда экспоненциальный рост не очевиден.
Этот закон может быть альтернативно объяснен тем фактом, что если действительно верно, что первая цифра имеет особое распределение, то оно должно не зависеть от величин, в которых оно измеряется. Это значит, что при переводе, к примеру, футов в ярды (умножение на константу), распределение должно остаться неизменным — это масштабная инвариантность, и единственное непрерывное распределение, которое выполняет это требование — то, в котором логарифм равномерно распределен.
К примеру, первая (не нулевая) цифра длины или расстояния объекта должна иметь такое же распределение независимо от того проводится ли измерение в футах, ярдах или чем-то другом. Но в ярде есть три фута, поэтому вероятность, что первая цифра длины в ярдах будет 1, должна быть такой же, как вероятность, что первая цифра длины в футах 3, 4 или 5. Применяя это ко всем возможным шкалам измерений дает логарифмическое распределение, и учитывая что log10(1) = 0 и log10(10) = 1 дает закон Бенфорда. То есть если есть распределение первой цифры, которое не зависит от единиц измерения, единственным распределением первой цифры может быть то, которое подчиняется закону Бенфорда.
Для чисел, взятых из определенного распределения, к примеру, значений IQ, ростов людей или других переменных, подчиняющихся нормальному распределению, закон не выполняется. Однако, если «перемешать» числа из множества подобных распределений, к примеру, взяв числа из газетных статей, закон Бенфорда снова проявится. Это также может быть доказано математически: если неоднократно «случайно» выбирать распределение вероятностей и потом случайно выбрать число согласно этому распределению, получившийся список будет подчиняться закону Бенфорда

Распределение первых цифр населения 237 стран мира. Черные точки — распределение Бенфорда.
В списке высот 58 высочайших строений мира в своей категории (по состоянию на сентябрь 2010) цифра «1» стоит на первой позиции намного чаще, чем цифра «9», независимо от единицы измерения:
| Первая цифра | Метры | Футы | ||
|---|---|---|---|---|
| Количество | % | Количество | % | |
| 1 | 27 | 47,4 % | 13 | 22,8 % |
| 2 | 8 | 14,0 % | 8 | 14,0 % |
| 3 | 7 | 12,3 % | 8 | 14,0 % |
| 4 | 5 | 8,8 % | 3 | 5,3 % |
| 5 | 2 | 3,5 % | 14 | 24,6 % |
| 6 | 3 | 5,3 % | 5 | 8,8 % |
| 7 | 2 | 3,5 % | 3 | 5,3 % |
| 8 | 3 | 5,3 % | 1 | 1,8 % |
| 9 | 0 | 0,0 % | 2 | 3,5 % |
Этот закон основывается на логарифмической природе многих процессов и явлений, что приводит к тому, что меньшие числа имеют большую вероятность быть первой цифрой, чем более большие числа. Закон Бенфорда нередко используется для проверки подлинности данных и обнаружения аномалий в бухгалтерских отчетах, налоговых декларациях и других числовых данных. Если, несмотря на соответствие параметрическим требованиям, наборы данных реального мира не соответствуют закону Бенфорда в том смысле, что количество вхождений определенной цифры значительно отклоняется от ожидаемого, установленного законом Бенфорда, то следователь подвергает эти наборы данных, начинающиеся с этой цифры, проверке. более глубокий анализ, чтобы найти причину (причины) этих расхождений. Эта быстрая процедура может привести к более глубокому пониманию особенностей исследуемого набора данных или к обнаружению манипуляций во время создания данных.
Однако следует отметить, что закон Бенфорда не всегда применим и не является абсолютной константой. В некоторых случаях данные могут расходиться с этим законом из-за специфики конкретных процессов или манипуляций с данными. Проверка распределения данных по закону Бенфорда используется для выявления злонамеренных манипуляций с данными, в том числе для выявления:
результаты сбора урожая

Распределение первых цифр таблицы с 87 номерами (см. текст)
В таблице представлены результаты сбора урожая 2002 года . На диаграмме синие столбцы указывают частоту появления первых цифр из 87 записанных чисел. Распределение Бенфорда показано красной линией. Оно отражает распределение гораздо лучше, чем равномерное распределение (зеленая линия). Несмотря на небольшую выборку, узнаваемо предпочтение малых значений первой цифры, как и тенденция второй цифры.
В таблице подведены итоги. Столбец 1-й цифры показывает, как часто цифра появляется на первом месте, столбец Бенфорда показывает, как часто она там ожидается согласно распределению Бенфорда. То же самое относится к количеству номеров с цифрой на втором месте в столбце 2-й цифры. Затем число 1 появляется на первой позиции 27 раз, ожидалось 26,19 раза. Число 4 появляется первым 17 раз, согласно Бенфорду, оно должно встречаться в среднем 8,43 раза.
По мере уменьшения разрядного значения цифры приведенное выше распределение Бенфорда все больше приближается к равномерному распределению цифр.
| цифра | 1-я цифра | Бенфорд | 2-я цифра | Бенфорд |
|---|---|---|---|---|
| 0 | — | — | 9 | 10:41 |
| 1 | 27 | 26:19 | 17 | 9,91 |
| 2 | 15 | 15:32 | 9 | 9,47 |
| 3 | 7 | 10,87 | 11 | 9.08 |
| 4 | 17 | 8,43 | 5 | 8,73 |
| 5 | 4 | 6,89 | 9 | 8:41 |
| 6 | 5 | 5,82 | 7 | 8:12 |
| 7 | 4 | 5.05 | 8-й | 7,86 |
| 8-й | 5 | 4,45 | 7 | 7,62 |
| 9 | 3 | 3,98 | 5 | 7,39 |
| всего | 87 | 87 |
Закон Бенфорда используется для обнаружения мошенничества при составлении балансовых отчетов, фальсификации счетов и вообще для быстрого выявления вопиющих нарушений в бухгалтерском учете. С помощью закона Бенфорда была раскрыта удивительно «креативная» система бухгалтерского учета в Enron и Worldcom , с помощью которой руководство выманивало у инвесторов их вклады (→ беловоротничковая преступность). Сегодня бухгалтеры и налоговые следователи используют методы, основанные на законе Бенфорда. Эти методы представляют собой важную часть математико-статистических методов, которые использовались в течение нескольких лет для выявления мошенничества в бухгалтерском учете, налогового мошенничества и мошенничества с инвесторами, а также мошенничества с данными в целом. Далее было показано, что первые цифры рыночных цен также подчиняются закону Бенфорда.
Закон Бенфорда также может помочь в обнаружении фальсификации данных в науке. Именно наборы данных из естественных наук привели к закону Бенфорда. Карл-Хайнц Тедтер из исследовательского центра Deutsche Bundesbank использовал тот же закон для обзора результатов 117 экономических статей в статье для German Economic Review .
Политологи использовали закон Бенфорда для изучения результатов нескольких федеральных выборов (с 1990 по 2005 год) на уровне округов и иногда (4 случая в 1500 тестах) обнаруживали значительные нарушения, касающиеся первого голосования. При проверке второго голосования, то есть прямых партийных выборов, нарушения были обнаружены в 51 из 190 тестов. По словам автора исследования Ахима Герреса, этот результат не является признаком манипуляций.
Также были обнаружены доказательства возможной фальсификации президентских выборов 2009 года в Иране .
Другие эксперты считают, что закон Бенфорда имеет ограниченное применение при изучении выборов.

Распределение размеров крупных городов Германии
На рисунке справа показано население 998 крупнейших городов Германии. Анализ Бенфорда дает следующие частоты начальных цифр:
| цифра | Измерено | Ожидал |
|---|---|---|
| 1 | 340 | 300,4 |
| 2 | 320 | 175,7 |
| 3 | 133 | 124,7 |
| 4 | 87 | 96,7 |
| 5 | 50 | 79,0 |
| 6 | 24 | 66,8 |
| 7 | 20 | 57,9 |
| 8-й | 12 | 51,1 |
| 9 | 12 | 45,7 |
Частота цифр 3 и 4 соответствует математическому ожиданию. С другой стороны, цифра 1 появляется чаще. Отклонение цифры 2 особенно выражено за счет цифр 7, 8 и 9, которые в первую очередь редко наблюдаются.
Опять же, этот пример показывает, что записи должны соответствовать определенным требованиям, чтобы претендовать на NBL; в настоящем наборе данных нет. Причиной этого является ограничение на города, распределение всех муниципалитетов должно привести к более точному совпадению. Кроме того, существует естественный минимальный размер поселения, а слияние муниципалитетов также оказывает влияние на распределение. Любопытно, что даже около 50% примеров, которые Бенфорд привел в своей публикации в качестве доказательства НБЛ, относятся к классу наборов данных, которые не имеют начальных цифр, распределенных по Бенфорду, но самое большее имеют примерно аналогичное распределение начальных цифр.
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ