6.2. Моменты нормального распределения кратко

Привет, Вы узнаете о том , что такое моменты нормального распределения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое моменты нормального распределения , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Выше мы доказали, что математическое ожидание случайной величины, подчиненной нормальному закону (6.1.1), равно 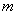, а среднее квадратическое отклонение равно .

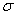Выведем общие формулы для центральных моментов любого порядка.

По определению:

.

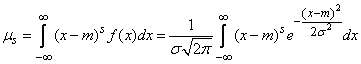Делая замену переменной

,

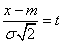получим:

.            (6.2.1)

Применив к выражению (6.2.1) формулу интегрирования по частям:

.

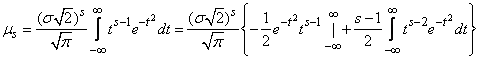Имея в виду, что  первый член внутри скобок равен нулю, получим:

.         (6.2.2)

Из формулы (6.2.1) имеем следующее выражение для :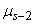

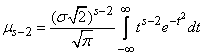.           (6.2.3)

Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем 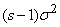; следовательно,

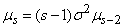. Об этом говорит сайт https://intellect.icu .             (6.2.4)

Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 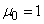 и 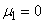, можно вычислить центральные моменты всех порядков. Так как 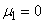, то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.

Для четных 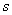 из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:

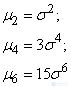
и т.д.

Общая формула для момента 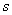-го порядка при любом четном  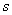имеет вид:

,

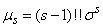где под символом 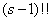 понимается произведение всех нечетных чисел от 1 до .

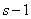Так как для нормального закона 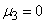, то асимметрия его также равна нулю:

.

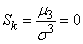Из выражения четвертого момента

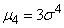
имеем:

,

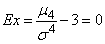т.е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса – характеризовать сравнительную крутость данного закона по сравнению с нормальным.

Информация, изложенная в данной статье про моменты нормального распределения , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое моменты нормального распределения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ