3.2. Теорема сложения вероятностей кратко

Привет, Вы узнаете о том , что такое теорема сложения вероятностей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теорема сложения вероятностей , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

теорема сложения вероятностей формулируется следующим образом.

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

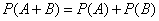.      (3.2.1)

 

Докажем теорему сложения вероятностей для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек:

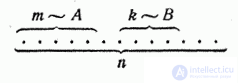
Предположим, что из этих случаев 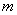 благоприятны событию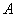, а – событию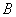. Тогда

Так как события 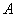 и 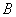несовместимы, то нет таких случаев, которые благоприятны 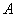и, и 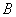вместе. Следовательно, событию  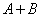благоприятны  случаев и

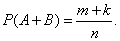
Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана.

Обобщим теорему сложения на случай трех событий. Обозначая событие 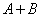 буквой 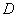, и присоединяя к сумме еще одно событие 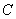, легко доказать, что

Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для n событий:

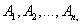
и докажем, что она будет справедлива для 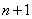 событий:

Обозначим:

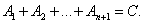
Имеем:

.

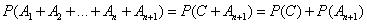Но так как для n событий мы считаем теорему уже доказанной, то

,

откуда

,

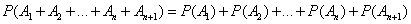что и требовалось доказать.

Таким образом, теорема сложения вероятностей применима к любому числу несовместных событий. Ее удобнее записать в виде:

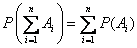.                   (3.2.2)

Отметим следствия, вытекающие из теоремы сложения вероятностей.

Следствие 1. Если события 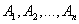 образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

.

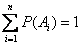Доказательство. Так как события 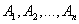 образуют полную группу, то появление хотя бы одного из них – достоверное событие:

.

Так как 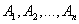 - несовместные события, то к ним применима теорема сложения вероятностей

,

откуда

,

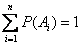что и требовалось доказать.

   Перед тем как вывести второе следствие теоремы сложения, определим понятие о «противоположных событиях».

Противоположными событиями называются два несовместных события, образующих полную группу.

Событие, противоположное событию 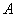, принято обозначать .

Примеры противоположных событий.

1) 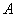 – попадание при выстреле,  - промах при выстреле;

2) 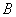– выпадение герба при бросании монеты,  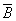- выпадение цифры при бросании монеты;

3) 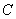– безотказная работа всех элементов технической системы,  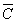- отказ хотя бы одного элемента;

4) 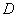– обнаружение не менее двух бракованных изделий в контрольной партии,  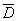- обнаружение не более одного бракованного изделия.

Следствие 2. Об этом говорит сайт https://intellect.icu . Сумма вероятностей противоположных событий равна единице:

.

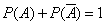Это следствие есть частный случай следствия 1. Оно выделено особо ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события , чем вероятность прямого события 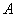. В этих случаях вычисляют  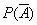и находят .

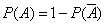Рассмотрим несколько примеров на применение теоремы сложения и ее следствий.

Пример 1. В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 100 билетов – выигрыши по 100 руб., на 50 билетов – выигрыши по 20 руб., на 100 билетов – выигрыши по 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб.

Решение. Рассмотрим события:

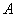– выиграть не менее 20 руб.,

 - выиграть 20 руб.,

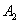- выиграть 100 руб.,

 - выиграть 500 руб.

Очевидно,

.

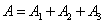По теореме сложения вероятностей

.

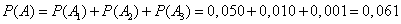Пример 2. Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.

Решение. Рассмотрим события:

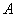– взрыв складов,

 - попадание в первый склад,

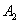- попадание во второй склад,

 -  попадание в третий склад.

Очевидно,

.

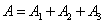Так как при сбрасывании одной бомбы события 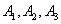  несовместны, то

.

Пример 3. Круговая мишень (рис. 3.2.1) состоит из трех зон: I, II и III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.

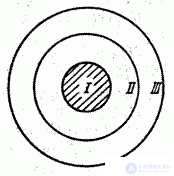
Рис. 3.2.1.

Решение. Обозначим 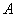– промах,  - попадание. Тогда

,

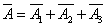где 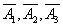 - попадание соответственно в первую, вторую и третью зоны

,

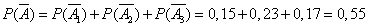откуда

.

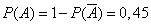Как уже указывалось, теорема сложения вероятностей (3.2.1) справедлива только для несовместных событий. В случае, когда события 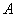 и 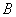 совместны, вероятность суммы этих событий выражается формулой

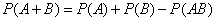.        (3.2.3)

В справедливости формулы (3.2.3) можно наглядно убедиться, рассматривая рисунок 3.2.2.

Рис. 3.2.2.

Аналогично вероятность суммы трех совместных событий вычисляется по формуле

.

Справедливость этой формулы также наглядно следует из геометрической интерпретации (рис. 3.2.3).

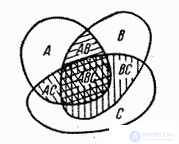
Рис. 3.2.3.

Методом полной индукции можно доказать общую формулу для вероятности суммы любого числа совместных событий:

,    (3.2.4)

где суммы распространяются на различные значения индексов 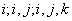, и т.д.

Формула (3.2.4) выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному, по два, по три и т.д.

Аналогичную формулу можно написать для произведения событий. Действительно, из рис. 3.2.2 непосредственно ясно, что

.     (3.2.5)

Из рис. 3.2.3 видно, что

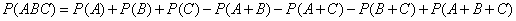.     (3.2.6)

Общая формула, выражающая вероятность произведения произвольного числа событий через вероятности сумм этих событий, взятых по одному, по два, по три и т.д., имеет вид:

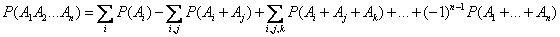.                   (3.2.7)

Формулы типа (3.2.4) и (3.2.7) находят практическое применение при преобразовании различных выражений, содержащих вероятности сумм и произведений событий. В зависимости от специфики задачи в некоторых случаях удобнее бывает пользоваться только суммами, а в других только произведениями событий: для преобразования одних в другие и служат подобные формулы.

Пример. Техническое устройство состоит из трех агрегатов: двух агрегатов первого типа -  и 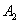- и одного агрегата второго типа – 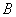. Агрегаты  и 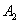дублируют друг друга: при отказе одного из них происходит автоматическое переключение на второй. Агрегат  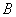не дублирован. Для того, чтобы устройство прекратило работу (отказало), нужно, чтобы одновременно отказали оба агрегата  и 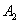 или же агрегат 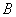. Таким образом, отказ устройства – событие  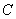– представляется в виде:

,

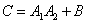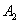где  - отказ агрегата , - отказ агрегата 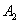,  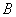– отказ агрегата .

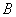Требуется выразить вероятность события 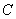 через вероятности событий, содержащих только суммы,  а не произведения элементарных событи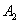й , и .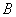

Решение. По формуле (3.2.3) имеем:

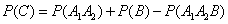;       (3.2.8)

по формуле (3.2.5)

;

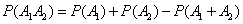по формуле (3.2.6)

.

Подставляя эти выражения в (3.2.8) и производя сокращения, получим:

.

 

Информация, изложенная в данной статье про теорема сложения вероятностей , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое теорема сложения вероятностей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про теорема сложения вероятностей