Пространство элементарных событий

Привет, сегодня поговорим про пространство элементарных событий, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое пространство элементарных событий , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

пространство элементарных событий  — множество 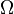 всех различных исходов случайного эксперимента.

Элемент этого множества 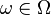 называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счетно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий  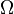вместе с алгеброй событий  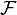и вероятностью  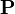образует тройку 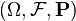, которая называется вероятностным пространством.

Элементарное событие[править ]

В теории вероятностей элементарные события или события-атомы — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается .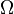

Всякое подмножество множества 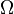 элементарных событий называется случайным событием. Об этом говорит сайт https://intellect.icu . Говорят, что в результате эксперимента произошло случайное событие 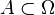, если (элементарный) исход эксперимента является элементом .

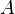В определении вероятностного пространства на множестве случайных событий вводится сигма-аддитивная конечная мера, называемая вероятностью.

Элементарные события могут иметь вероятности, которые строго положительны, нули, неопределенны, или любая комбинация из этих вариантов. Например, любоедискретное вероятностное распределение определяется вероятностями того, что может быть названо элементарными событиями. Напротив, все элементарные события имеют вероятность нуль для непрерывного распределения. Смешанные распределения, не будучи ни непрерывными, ни дискретными, могут содержатьатомы, которые могут мыслиться как элементарные (то есть события-атомы) события с ненулевой вероятностью. В теории меры в определении вероятностного пространства вероятность произвольного элементарного события не могла быть определена до тех пор, пока математики не увидели различие между пространством исходов S и событиями, которые представляют интерес, и которые определяются как элементы σ-алгебры событий из S.

Формально говоря, элементарное событие — это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это все еще множество, но не сам элемент. Однако элементарные события обычно записываются как элементы, а не как множества с целью упрощения, когда это не может вызвать недоразумения.

Примеры

Примеры пространств исходов эксперимента, 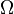, и элементарных событий:

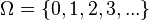• Если объекты счетны, а пространство исходов  (натуральные числа), то элементарные события — это любые множества 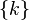, где .
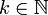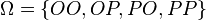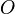• Если монета бросается дважды, ,  для орла, а  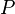для решки, то элементарные события: 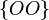, , 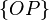 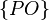и .
• Если 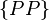 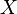— это нормально распределенные случайные величины, 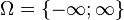, реальные числа, то элементарные события — любые множества 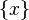, где 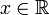. Этот пример показывает, что непрерывное вероятностное распределение не определяется вероятностями событий-атомов, поскольку здесь вероятности всех элементарных событий равны нулю.

Надеюсь, эта статья про пространство элементарных событий, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое пространство элементарных событий и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ