5.8. Закон равномерной плотности кратко

Привет, Вы узнаете о том , что такое закон равномерной плотности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон равномерной плотности , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В некоторых задачах практики встречаются непрерывно случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью распределения вероятности). О таких случайных величинах говорят, что они распределены по закону равномерной плотности.

 

Приведем несколько примеров подобных случайных величин.

Пример 1. Произведено взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее 1г; результат взвешивания показывает, что вес тела заключен между 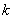и граммами. Вес тела принят равным  граммам. Допущенная при этом ошибка 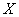, очевидно, есть случайная величина, распределенная с равномерной плотностью на участке 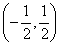г.

Пример 2. Вертикально поставленное симметричное колесо (рис. 5.8.1) приводится во вращение и затем останавливается вследствие трения. Рассматривается случайная величина 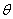 - угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса ОА. Очевидно, величина  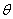распределена с равномерной плотностью на участке .

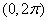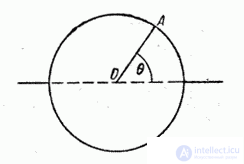
Рис. 5.8.1.

Пример 3. Поезда метро идут с интервалом 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Т, в течение которого ему придется ждать поезда, представляет собой случайную величину, распределенную с равномерной плотностью на участке (0,2) минут.

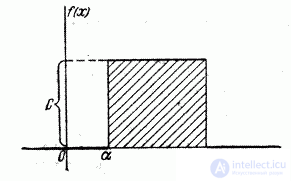
Рис. 5.8.2.

Рассмотрим случайную величину 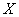, подчиненную закону равномерной плотности на участке от  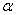до 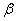 (рис. Об этом говорит сайт https://intellect.icu . 5.8.2), и напишем для нее выражение плотности распределения 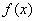. Плотность  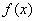постоянна и равна с на отрезке 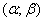; вне этого отрезка она равна нулю:

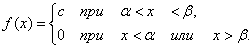
Так как площадь, ограниченная кривой распределения, равна единице:

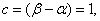
то

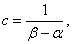
и плотность распределения 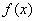 имеет вид:

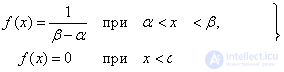            (5.8.1)

Формула (5.8.1) и выражает закон равномерной плотности на участке .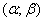

Напишем выражение для функции распределения . Функция распределения выражается площадью кривой распределения, лежащей левее точки 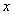. Следовательно,

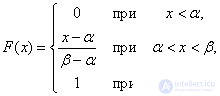
График функции приведен на рис. 5.8.3.

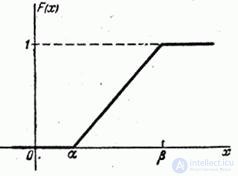
Рис. 5.8.3.

Определим основные числовые характеристики случайной величины 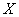, подчиненной закону равномерной плотности на участке от  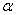до .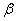

Математическое ожидание величины Х:

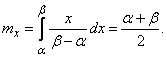           (5.8.2)

В силу симметричности равномерного распределения медиана величины 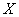 также равна .

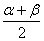Моды закон равномерности плотности не имеет.

По формуле (5.7.16) находим дисперсию величины :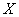

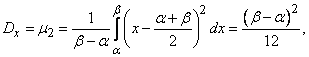             (5.8.3)

откуда среднее квадратическое отклонение

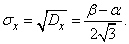              (5.8.4)

В силу симметричности распределения его асимметрия равна нулю:

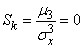.                  (5.8.5)

Для определения эксцесса находим четвертый центральный момент:

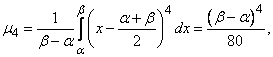
откуда

                   (5.8.6)

Определяем среднее арифметическое отклонение:

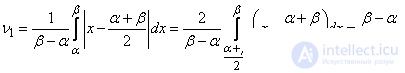         (5.8.7)

Наконец, найдем вероятность попадания случайной величины 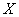, распределенной по закону равномерной плотности, на участок 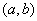, представляющий собой часть участка  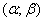(рис. 5.8.4). Геометрически эта вероятность представляет собой площадь, заштрихованную на рис. 5.8.4. Очевидно, она равна:

           (5.8.8)

т.е. отношению длины отрезка 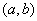 ко всей длине участка 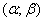, на котором задано равномерное распределение.

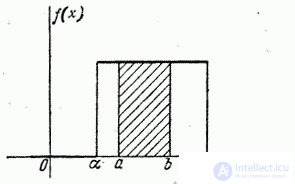
Рис. 5.8.4.

Информация, изложенная в данной статье про закон равномерной плотности , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое закон равномерной плотности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про закон равномерной плотности