Лекция
Привет, Вы узнаете о том , что такое формулы выражающие центральную предельную теорему, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое формулы выражающие центральную предельную теорему, встречающиеся при ее практическом применении , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Согласно центральной предельной теореме, закон распределения суммы достаточно большого числа независимых случайных величин (при соблюдении некоторых нежестких ограничений) сколь угодно близок к нормальному.
Практически центральной предельной теоремой можно пользоваться и тогда, когда речь идет о сумме сравнительно небольшого числа случайных величин. При суммировании независимых случайных величин, сравнимых по своему рассеиванию, с увеличением числа слагаемых закон распределения суммы очень скоро становится приблизительно нормальным. На практике вообще широко применяется приближенная замена одних законов распределения другими; при той сравнительно малой точности, которая требуется от вероятностных расчетов, такая замена тоже может быть сделана крайне приближенно. Опыт показывает, что когда число слагаемых порядка десяти (а часто и меньше), закон распределения суммы обычно может быть заменен нормальным.
В практических задачах часто применяют центральную предельную теорему для вычисления вероятности того, что сумма нескольких случайных величин окажется в заданных пределах.
Пусть 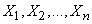 - независимые случайные величины с математическими ожиданиями
- независимые случайные величины с математическими ожиданиями
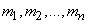
и дисперсиями
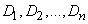 .
.
Предположим, что условия центральной предельной теоремы выполнены (величины 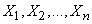 сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых
сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых  достаточно для того, чтобы закон распределения величины
достаточно для того, чтобы закон распределения величины
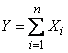 (13.9.1)
(13.9.1)
можно было считать приближенно нормальным.
Тогда вероятность того, что случайная величина  попадает в пределы участка
попадает в пределы участка  , выражается формулой
, выражается формулой
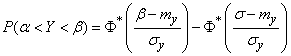 , (13.9.2)
, (13.9.2)
где 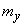 ,
, 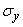 - математическое ожидание и среднее квадратическое отклонение величины
- математическое ожидание и среднее квадратическое отклонение величины 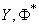 - нормальная функция распределения.
- нормальная функция распределения.
Согласно теоремам сложения математических ожиданий и дисперсий
 (13.9.3)
(13.9.3)
Таким образом, для того чтобы приближенно найти вероятности попадания суммы большого числа случайных величин на заданный участок, не требуется знать законы распределения этих величин; достаточно знать лишь их характеристики. Разумеется, это относится только к случаю, когда выполнено основное условие центральной предельной теоремы - равномерно малое влияние слагаемых на рассеивание суммы.
Кроме формул типа (13.9.2), на практике часто применяются формулы, в которых вместо суммы случайных величин 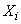 фигурирует их нормированная сумма
фигурирует их нормированная сумма
 . (13.9.4)
. (13.9.4)
Очевидно,
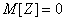 ;
; 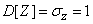 .
.
Если закон распределения величины  близок к нормальному с параметрами (13.9.3), то закон распределения величины
близок к нормальному с параметрами (13.9.3), то закон распределения величины 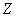 близок к нормальному с параметрами
близок к нормальному с параметрами 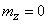 ,
, 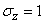 . Отсюда
. Отсюда
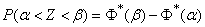 . (13.9.5)
. (13.9.5)
Заметим, что центральная предельная теорема может применяться не только к непрерывным, но и к дискретным случайным величинам при условии, что мы будем оперировать не плотностями, а функциями распределения. Действительно, если величины 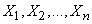 дискретны, то их сумма
дискретны, то их сумма  - также дискретная случайная величина и поэтому, строго говоря, не может подчиняться нормальному закону. Однако все формулы типа (13.9.2), (13.9.5) остаются в силе, так как в них фигурируют не плотности, а функции распределения. Можно доказать, что если дискретные случайные величины удовлетворяют условиям центральной предельной теоремы, то функция распределения их нормированной суммы
- также дискретная случайная величина и поэтому, строго говоря, не может подчиняться нормальному закону. Однако все формулы типа (13.9.2), (13.9.5) остаются в силе, так как в них фигурируют не плотности, а функции распределения. Можно доказать, что если дискретные случайные величины удовлетворяют условиям центральной предельной теоремы, то функция распределения их нормированной суммы 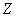 (см. Об этом говорит сайт https://intellect.icu . формулу (13.9.4)) при увеличении
(см. Об этом говорит сайт https://intellect.icu . формулу (13.9.4)) при увеличении  неограниченно приближается к нормальной функции распределения с параметрами
неограниченно приближается к нормальной функции распределения с параметрами 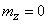 ,
, 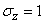 .
.
Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема Лапласа.
Если производится  независимых опытов, в каждом из которых событие
независимых опытов, в каждом из которых событие 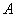 появляется с вероятностью
появляется с вероятностью 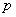 , то справедливо соотношение
, то справедливо соотношение
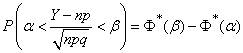 , (13.9.6)
, (13.9.6)
где  - число появлений события
- число появлений события 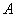 в
в  опытах,
опытах, 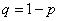 .
.
Доказательство. Пусть производится  независимых опытов, в каждом из которых с вероятностью
независимых опытов, в каждом из которых с вероятностью 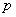 может появиться событие
может появиться событие 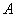 . Представим случайную величину
. Представим случайную величину  - общее число появлений события в
- общее число появлений события в  опытах - в виде суммы
опытах - в виде суммы
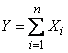 , (13.9.7)
, (13.9.7)
где 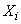 - число появлений события
- число появлений события 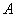 в
в  -м опыте.
-м опыте.
Согласно доказанной в 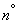 13.8 теореме, закон распределения суммы одинаково распределенных слагаемых при увеличении их числа приближается к нормальному закону. Следовательно, при достаточно большом
13.8 теореме, закон распределения суммы одинаково распределенных слагаемых при увеличении их числа приближается к нормальному закону. Следовательно, при достаточно большом  справедлива формула (13.9.5), где
справедлива формула (13.9.5), где
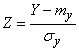 . (13.9.8)
. (13.9.8)
В 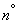 10.3 мы доказали, что математическое ожидание и дисперсия числа появлений события в
10.3 мы доказали, что математическое ожидание и дисперсия числа появлений события в  независимых опытах равны:
независимых опытах равны:
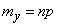 ;
; 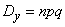
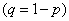 .
.
Подставляя эти выражения в (13.9.8), получим
 ,
,
и формула (13.9.5) примет вид:
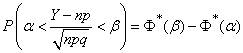 .
.
Теорема доказана.
Пример 1. По полосе укреплений противника сбрасывается 100 серий бомб. При сбрасывании одной такой серии математическое ожидание числа попаданий равно 2, а среднее квадратическое отклонение числа попаданий равно 1,5. Найти приближенно вероятность того, что при сбрасывании 100 серий в полосу попадает от 180 до 220 бомб.
Решение. Представим общее число попаданий как сумму чисел попаданий бомб в отдельных сериях:
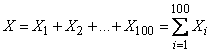 ,
,
где 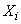 - число попаданий
- число попаданий  -й серии.
-й серии.
Условия центральной предельной теоремы соблюдены, так как величины 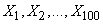 распределены одинаково. Будем считать число
распределены одинаково. Будем считать число 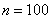 достаточным для того, чтобы можно было применить предельную теорему (на практике она обычно применима и при гораздо меньших
достаточным для того, чтобы можно было применить предельную теорему (на практике она обычно применима и при гораздо меньших  ). Имеем:
). Имеем:
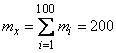 ,
, 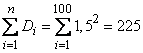 .
.
Применяя формулу (13.9.6), получим:
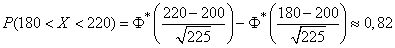 ,
,
т. е. с вероятностью 0,82 можно утверждать, что общее число попадании в полосу не выйдет за пределы 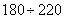 .
.
Пример 2. Происходит групповой воздушный бой, в котором участвуют 50 бомбардировщиков и 100 истребителей. Каждый бомбардировщик атакуется двумя истребителями; таким образом, воздушный бой распадается на 50 элементарных воздушных боев, в каждом из которых участвует один бомбардировщик и два истребителя. В каждом элементарном бою вероятность сбития бомбардировщика равна 0,4; вероятность того, что в элементарном бою будут сбиты оба истребителя, равна 0,2: вероятность того, что будет сбит ровно один истребитель, равна 0,5. Требуется: 1) найти вероятность того, что в воздушном бою будет сбито не менее 35% бомбардировщиков; 2) оценить границы, в которых с вероятностью 0,9 будет заключено число сбитых истребителей.
Решение. 1) Обозначим  - число сбитых бомбардировщиков;
- число сбитых бомбардировщиков;
 ,
,
где 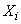 - число бомбардировщиков, сбитых в
- число бомбардировщиков, сбитых в  -м элементарном бою.
-м элементарном бою.
Ряд распределения величины 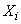 имеет вид:
имеет вид:
|
|
|
|
|
|
Отсюда
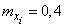 ;
; 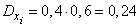 ;
; 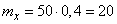 ;
; 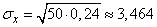 .
.
Применяя формулу (13.9.6) и полагая  (или, что в данном случае равносильно,
(или, что в данном случае равносильно,  ),
), 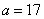 , находим:
, находим:
 .
.
2) Обозначим  число сбитых истребителей:
число сбитых истребителей:
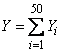 ,
,
где 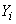 - число истребителей, сбитых в
- число истребителей, сбитых в  -м элементарном бою.
-м элементарном бою.
Ряд распределения величины 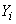 имеет вид:
имеет вид:
|
|
|
|
|
|
|
|
Отсюда находим математическое ожидание и дисперсию величины 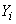 :
:
 ;
; 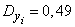 .
.
Для величины  :
:
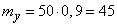 ;
; 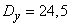 ;
; 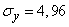 .
.
Определим границы участка, симметричного относительно  , в который с вероятностью 0,9 попадет величина
, в который с вероятностью 0,9 попадет величина  . Обозначим половину длины этого участка
. Обозначим половину длины этого участка 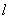 . Тогда
. Тогда
 ,
,
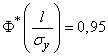 .
.
По таблицам функции 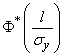 находим то значение аргумента, для которого
находим то значение аргумента, для которого 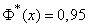 ; это значение приближенно равно
; это значение приближенно равно
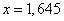 ,
,
т.е.
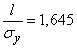 ,
,
откуда
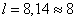 .
.
Следовательно, с вероятностью около 0,9 можно утверждать, что число сбитых истребителей будет заключено в предела 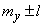 , т. е. в пределах от 37 до 53.
, т. е. в пределах от 37 до 53.
Информация, изложенная в данной статье про формулы выражающие центральную предельную теорему , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое формулы выражающие центральную предельную теорему, встречающиеся при ее практическом применении и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про формулы выражающие центральную предельную теорему
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ