5.3. Вероятность попадания случайной величины на заданный участок кратко

Привет, Вы узнаете о том , что такое вероятность попадания случайной величины на заданный участок, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вероятность попадания случайной величины на заданный участок , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

При решении практических задач, связанных со случайными величинами, часто оказывается необходимым вычислить вероятность того, что случайная величина примет значение, заключенное в некоторых пределах, например, от 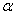 до 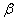. Это событие мы будем называть «попаданием случайной величины  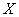на участок от  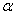до ».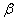

 

Условимся для определенности левый конец 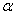 включать в участок , а правый – не включать. Тогда попадание случайной величины 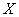 на участок  равносильно выполнению неравенства:

.

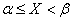Выразим вероятность этого события через функцию распределения величины 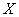. Для этого рассмотрим три события:

событие А, состоящее в том, что ;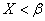

событие В, состоящее в том, что ;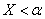

событие С, состоящее в том, что .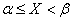

Учитывая, что 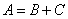, по теореме сложения вероятностей имеем:

,

или

,

откуда

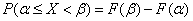,          (5.3.1)

т.е. Об этом говорит сайт https://intellect.icu . вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке.

Будем неограниченно уменьшать участок , полагая, что . В пределе вместо вероятности попадания на участок получим вероятность того, что величина примет отдельно взятое значение :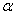

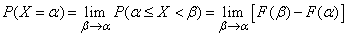.        (5.3.2)

Значение этого предела зависит от того, непрерывна ли функция 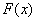 в точке  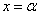или же терпит разрыв. Если в точке  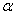функция  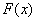имеет разрыв, то предел (5.3.2.) равен значению скачка функции  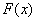в точке 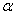. Если же функция  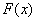в точке  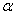непрерывна, то этот предел равен нулю.

В дальнейшем изложении мы условимся называть «непрерывными» только те случайные величины, функция распределения которых везде непрерывна. Имея это в виду, можно сформулировать следующее положение:

Вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Остановимся на этом положении несколько подробнее. В данном курсе мы уже встречались с событиями, вероятности которых были равны нулю: это были невозможные события. Теперь мы видим, что обладать нулевой вероятностью могут не только невозможные, но и возможные события. Действительно, событие 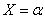, состоящее в том, что непрерывная случайная величина  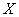примет значение 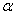, возможно, однако вероятность его равна нулю. Такие события – возможные, но с нулевой вероятностью – появляются только при рассмотрении опытов, не сводящихся к схеме случаев.

Понятие о событии «возможном, но обладающем нулевой вероятностью» кажется на первый взгляд парадоксальным. В действительности оно не более парадоксально, чем представление о теле, имеющем определенную массу, тогда как ни одна из точек внутри тела  определенной конечной массой не обладает. Сколь угодно  малый объем, выделенный из тела, обладает определенной конечной массой; эта масса приближается к нулю по мере уменьшения объема и в пределе равна нулю до точки. Аналогично при непрерывном распределении вероятностей вероятность попадания на сколь угодно малый участок может быть отлична от нуля, тогда как вероятность попадания в строго определенную точку в точности равна нулю.

Если производится опыт, в котором непрерывная случайная величина 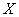 должна принять одно из своих возможных значений, то до опыта вероятность каждого из таких значений равна нулю; однако в исходе опыта случайная величина  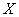непременно примет одно из своих возможных значений, т. е. заведомо произойдет одно из событий, вероятности которых были равны нулю.

Из того, что событие 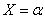 имеет вероятность, равную нулю, вовсе не следует, что это событие не будет появляться, т.е. что частота этого события равна нулю. Мы знаем, что частота события при большом числе опытов не равна, а только приближается к вероятности. Из того, что вероятность события  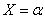равна нулю, следует только, что при неограниченном повторении опыта это событие будет появляться сколь угодно редко.

Если событие 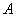 в данном опыте возможно, но имеет вероятность, равную нулю, то противоположное ему событие  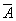имеет вероятность, равную единице, но недостоверно. Для непрерывной случайной величины  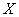при любом  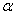событие  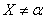имеет вероятность, равную единице, однако это событие не достоверно. Такое событие при неограниченном повторении опыта будет происходить почти всегда, но не всегда.

В n° 5.1 мы познакомились с «механической» интерпретацией прерывной случайной величины как распределения единичной массы, сосредоточенной в нескольких изолированных точках на оси абсцисс. В случае непрерывной случайной величины механическая интерпретация сводится к распределению единичной массы не по отдельным точкам, а непрерывно по оси абсцисс, причем ни одна точка не обладает конечной массой.

Информация, изложенная в данной статье про вероятность попадания случайной величины на заданный участок , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое вероятность попадания случайной величины на заданный участок и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про вероятность попадания случайной величины на заданный участок