Лекция
Привет, Вы узнаете о том , что такое нормальный закон распределения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое нормальный закон распределения, его параметры , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т.д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.
Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.
Нормальный закон распределения характеризуется плотностью вероятности вида:
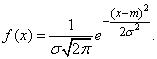 (6.1.1)
(6.1.1)
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная 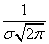 , соответствует точке
, соответствует точке 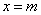 ; по мере удаления от точки
; по мере удаления от точки  плотность распределения падает, и при
плотность распределения падает, и при 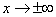 кривая асимптотически приближается к оси абсцисс.
кривая асимптотически приближается к оси абсцисс.

Рис. 6.1.1.
Выясним смысл численных параметров  и
и 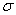 , входящих в выражение нормального закона (6.1.1); докажем, что величина
, входящих в выражение нормального закона (6.1.1); докажем, что величина  есть не что иное, как математическое ожидание, а величина
есть не что иное, как математическое ожидание, а величина 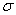 - среднее квадратическое отклонение величины
- среднее квадратическое отклонение величины  . Об этом говорит сайт https://intellect.icu . Для этого вычислим основные числовые характеристики величины
. Об этом говорит сайт https://intellect.icu . Для этого вычислим основные числовые характеристики величины  - математическое ожидание и дисперсию.
- математическое ожидание и дисперсию.
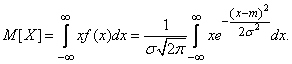
Применяя замену переменной
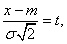
имеем:
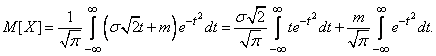 (6.1.2)
(6.1.2)
Нетрудно убедиться, что первый из двух интервалов в формуле (6.1.2) равен нулю; второй представляет собой известный интеграл Эйлера-Пуассона:
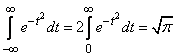 . (6.1.3)
. (6.1.3)
Следовательно,
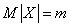 ,
,
т.е. параметр  представляет собой математическое ожидание величины
представляет собой математическое ожидание величины  . Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно – ц. р.).
. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно – ц. р.).
Вычислим дисперсию величины  :
:
 .
.
Применив снова замену переменной
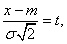
имеем:
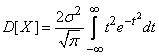 .
.
Интегрируя по частям, получим:
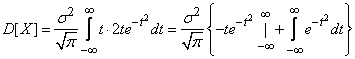 .
.
Первое слагаемое в фигурных скобках равно нулю (так как 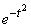 при
при 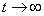 убывает быстрее, чем возрастает любая степень
убывает быстрее, чем возрастает любая степень  ), второе слагаемое по формуле (6.1.3) равно
), второе слагаемое по формуле (6.1.3) равно  , откуда
, откуда
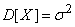 .
.
Следовательно, параметр 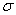 в формуле (6.1.1) есть не что иное, как среднее квадратическое отклонение величины
в формуле (6.1.1) есть не что иное, как среднее квадратическое отклонение величины  .
.
Выясним смысл параметров  и
и 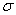 нормального распределения. Непосредственно из формулы (6.1.1) видно, что центром симметрии распределения является центр рассеивания
нормального распределения. Непосредственно из формулы (6.1.1) видно, что центром симметрии распределения является центр рассеивания  . Это ясно из того, что при изменении знака разности
. Это ясно из того, что при изменении знака разности  на обратный выражение (6.1.1) не меняется. Если изменять центр рассеивания
на обратный выражение (6.1.1) не меняется. Если изменять центр рассеивания  , кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
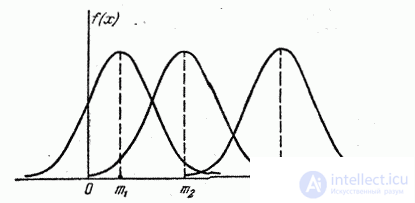
Рис. 6.1.2.
Размерность центра рассеивания – та же, что размерность случайной величины  .
.
Параметр 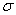 характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна
характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна 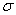 ; при увеличении
; при увеличении 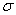 максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении
максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении 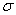 кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении
кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении 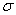 кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (I, II, III) при
кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (I, II, III) при 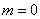 ; из них кривая I соответствует самому большому, а кривая III – самому малому значению
; из них кривая I соответствует самому большому, а кривая III – самому малому значению 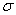 . Изменение параметра
. Изменение параметра 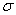 равносильно изменению масштаба кривой распределения – увеличению масштаба по одной оси и такому же уменьшению по другой.
равносильно изменению масштаба кривой распределения – увеличению масштаба по одной оси и такому же уменьшению по другой.
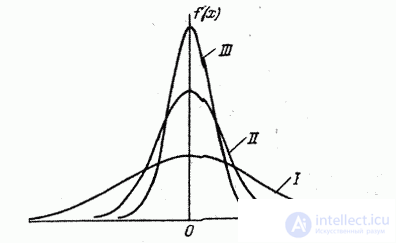
Рис. 6.1.3.
Размерность параметра 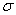 , естественно, совпадает с размерностью случайной величины
, естественно, совпадает с размерностью случайной величины  .
.
В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению 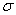 :
:
 .
.
Размерность меры точности обратная размерности случайной величины.
Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности 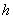 , можно записать нормальный закон в виде:
, можно записать нормальный закон в виде:
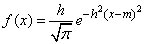 .
.
Информация, изложенная в данной статье про нормальный закон распределения , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое нормальный закон распределения, его параметры и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про нормальный закон распределения
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ