Лекция
Привет, Вы узнаете о том , что такое применения теорем о числовых характеристиках, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое применения теорем о числовых характеристиках , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
В данном  мы продемонстрируем применение аппарата числовых характеристик к решению ряда задач. Некоторые из этих задач имеют самостоятельное теоретическое значение и найдут применение в дальнейшем. Другие задачи носят характер примеров и приводятся для иллюстрации выведенных общих формул на конкретном цифровом материале.
мы продемонстрируем применение аппарата числовых характеристик к решению ряда задач. Некоторые из этих задач имеют самостоятельное теоретическое значение и найдут применение в дальнейшем. Другие задачи носят характер примеров и приводятся для иллюстрации выведенных общих формул на конкретном цифровом материале.
Задача 1. Коэффициент корреляции линейно зависимых случайных величин.
Доказать, что если случайные величины  и
и  связаны линейной функциональной зависимостью
связаны линейной функциональной зависимостью
 ,
,
то их коэффициент корреляции равен 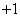 или
или  , смотря по знаку коэффициента
, смотря по знаку коэффициента  .
.
Решение. Имеем:

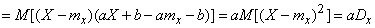 ,
,
где 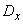 - дисперсия величины
- дисперсия величины  .
.
Для коэффициента корреляции имеем выражение:
 . (10.3.1)
. (10.3.1)
Для определения  найдем дисперсию величины
найдем дисперсию величины  :
:
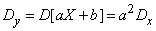 ,
,
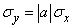 .
.
Подставляя в формулу (10.3.1), имеем:
 .
.
Величина  равна
равна 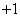 , когда
, когда  положительно, и
положительно, и  , когда
, когда  отрицательно, что и требовалось доказать.
отрицательно, что и требовалось доказать.
Задача 2. Границы коэффициента корреляции.
Доказать, что для любых случайных величин
 .
.
Решение. Рассмотрим случайную величину:
 ,
,
где  - средние квадратические отклонения величин
- средние квадратические отклонения величин 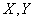 . Определим дисперсию величины
. Определим дисперсию величины  . По формуле (10.2.13) имеем:
. По формуле (10.2.13) имеем:
 ,
,
или
 .
.
Так как дисперсия любой случайной величины не может быть отрицательна, то
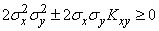 ,
,
или
 ,
,
откуда
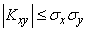 ,
,
а следовательно,
 ,
,
что и требовалось доказать.
Задача 3. Проектирование случайной точки на плоскости на произвольную прямую.
Дана случайная точка на плоскости с координатами  (рис. 10.3.1). Спроектируем эту точку на ось
(рис. 10.3.1). Спроектируем эту точку на ось  , проведенную через начало координат под углом
, проведенную через начало координат под углом  к оси
к оси  . Проекция точки
. Проекция точки  на ось
на ось  также есть случайная точка; ее расстояние
также есть случайная точка; ее расстояние  от начала координат есть случайная величина. Требуется найти математическое ожидание и дисперсию величины
от начала координат есть случайная величина. Требуется найти математическое ожидание и дисперсию величины  .
.

Рис.10.3.1
Решение. Имеем:
 .
.
Так как  есть линейная функция аргументов
есть линейная функция аргументов  и
и  , то
, то
 ;
;

 ,
,
где  - дисперсии и корреляционный момент величин
- дисперсии и корреляционный момент величин  .
.
Переходя к средним квадратическим отклонениям, получим:
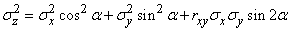 . (10.3.2)
. (10.3.2)
В случае некоррелированных случайных величин (при  )
)
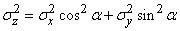 . (10.3.3)
. (10.3.3)
Задача 4. Математическое ожидание числа появлений события при нескольких опытах.
Производится  опытов, в каждом из которых может появиться или не появиться событие
опытов, в каждом из которых может появиться или не появиться событие  . Вероятность появления события
. Вероятность появления события  в
в  -м опыте равна
-м опыте равна  . Найти математическое ожидание числа появлений события.
. Найти математическое ожидание числа появлений события.
Решение. Рассмотрим прерывную случайную величину  - число появлений события во всей серии опытов. Очевидно,
- число появлений события во всей серии опытов. Очевидно,
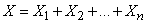 ,
,
где 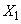 - число появлений события в первом опыте,
- число появлений события в первом опыте,
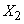 - число появлений события во втором опыте,
- число появлений события во втором опыте,
………………………………………………….
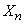 - число появлений события в
- число появлений события в  -м опыте,
-м опыте,
или, короче,
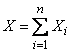 ,
,
где  - число появлений события в
- число появлений события в 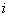 -м опыте.
-м опыте.
Каждая из величин  есть прерывная случайная величина с двумя возможными значениями:
есть прерывная случайная величина с двумя возможными значениями:  и
и  . Ряд распределения величины
. Ряд распределения величины  имеет вид:
имеет вид:
|
|
|
|
|
|
(10.3.4)
где 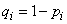 - вероятность непоявления события
- вероятность непоявления события  в
в  -м опыте.
-м опыте.
По теореме сложения математических ожиданий
 , (10.3.5)
, (10.3.5)
где  - математическое ожидание величины
- математическое ожидание величины  .
.
Вычислим математическое ожидание величины  . По определению математического ожидания
. По определению математического ожидания
 .
.
Подставляя это выражение в формулу (10.3.5), имеем
 , (10.3.6)
, (10.3.6)
т. е. математическое ожидание числа появлений события при нескольких опытах равно сумме вероятностей события в отдельных опытах.
В частности, когда условия опытов одинаковы и
 ,
,
формула (10.3.5) принимает вид
 . (10.3.7)
. (10.3.7)
Так как теорема сложения математических ожиданий применима к любым случайным величинам - как зависимым, так и независимым, формулы (10.3.6) и (10.3.7) применимы к любым опытам - зависимым и независимым.
Выведенная теорема часто применяется в теории стрельбы, когда требуется найти среднее число попаданий при нескольких выстрелах - зависимых или независимых. Математическое ожидание числа попаданий при нескольких выстрелах равно сумме вероятностей попадания при отдельных выстрелах.
Задача 5. Дисперсия числа появлений события при нескольких независимых опытах.
Производится  независимых опытов, в каждом из которых может появиться событие
независимых опытов, в каждом из которых может появиться событие  , причем вероятность появления события
, причем вероятность появления события  в
в 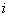 -м опыте равна
-м опыте равна  . Найти дисперсию и среднее квадратическое отклонение числа появлений события
. Найти дисперсию и среднее квадратическое отклонение числа появлений события  .
.
Решение. Рассмотрим случайную величину  - число появлений события
- число появлений события  . Так же как в предыдущей задаче, представим величину
. Так же как в предыдущей задаче, представим величину  в виде суммы:
в виде суммы:
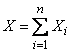 ,
,
где  - число появлений события в
- число появлений события в 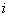 -м опыте.
-м опыте.
В силу независимости опытов случайные величины 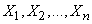 независимы и к ним применима теорема сложения дисперсий:
независимы и к ним применима теорема сложения дисперсий:
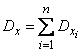 .
.
Найдем дисперсию случайной величины  . Из ряда распределения (10.3.4) имеем:
. Из ряда распределения (10.3.4) имеем:
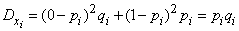 ,
,
откуда
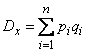 , (10.3.8)
, (10.3.8)
т. е. дисперсия числа появлений события при нескольких независимых опытах равна сумме вероятностей появления и непоявления события в каждом опыте.
Из формулы (10.3.8) находим среднее квадратическое отклонение числа появлений события  :
:
 . (10.3.9)
. (10.3.9)
При неизменных условиях опытов, когда  , формулы (10.3.8) и (10.3.9) упрощаются и принимают вид:
, формулы (10.3.8) и (10.3.9) упрощаются и принимают вид:
 (10.3.10)
(10.3.10)
Задача 6. Дисперсия числа появлений события при зависимых опытах.
Производится  зависимых опытов, в каждом из которых может появиться событие
зависимых опытов, в каждом из которых может появиться событие  , причем вероятность события
, причем вероятность события  в
в 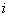 -м опыте равна
-м опыте равна 
 . Определить дисперсию числа появлений события.
. Определить дисперсию числа появлений события.
Решение. Для того чтобы решить задачу, снова представим число появлений события  в виде суммы:
в виде суммы:
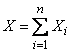 , (10.3.11)
, (10.3.11)
где

Так как опыты зависимы, то нам недостаточно задать вероятности

того, что событие  произойдет в первом, втором, третьем и т. д. опытах. Нужно еще задать характеристики зависимости опытов. Оказывается, для решения нашей задачи достаточно задать вероятности
произойдет в первом, втором, третьем и т. д. опытах. Нужно еще задать характеристики зависимости опытов. Оказывается, для решения нашей задачи достаточно задать вероятности 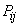 совместного появления события
совместного появления события  как в
как в 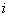 -м, так и в
-м, так и в  -м опыте:
-м опыте:  . Предположим, что эти вероятности заданы. Применим к выражению (10.3.11) теорему о дисперсии суммы (формулу (10.2.10)):
. Предположим, что эти вероятности заданы. Применим к выражению (10.3.11) теорему о дисперсии суммы (формулу (10.2.10)):
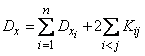 , (10.3.12)
, (10.3.12)
где  - корреляционный момент величин
- корреляционный момент величин  :
:
 .
.
По формуле (10.2.19)
 . (10.3.13)
. (10.3.13)
Рассмотрим случайную величину  . Очевидно она равна нулю, если хотя бы одна из величин
. Очевидно она равна нулю, если хотя бы одна из величин  равна нулю, т. е. хотя бы в одном из опытов (
равна нулю, т. е. хотя бы в одном из опытов (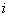 -м или
-м или  -м) событие
-м) событие  не появилось. Для того чтобы величина
не появилось. Для того чтобы величина  была равна единице, требуется, чтобы в обоих опытах (
была равна единице, требуется, чтобы в обоих опытах (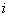 -м и
-м и  -м) событие
-м) событие  появилось. Вероятность этого равна
появилось. Вероятность этого равна 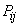 . Следовательно,
. Следовательно,
 ,
,
и
 .
.
Подставляя это выражение в формулу (10.3.12), получим:
 . (10.3.14)
. (10.3.14)
Формула (10.3.14) и выражает дисперсию числа появлений события при зависимых опытах. Проанализируем структуру этой формулы. Первый член в правой части формулы представляет собой дисперсию числа появлений события при независимых опытах, а второй дает «поправку на зависимость». Если вероятность 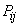 равна
равна  , то эта поправка равна нулю. Если вероятность
, то эта поправка равна нулю. Если вероятность 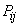 больше, чем
больше, чем  , это значит, что условная вероятность появления события
, это значит, что условная вероятность появления события  в
в  -м опыте при условии, что в
-м опыте при условии, что в 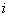 -м опыте оно появилось, больше, чем простая (безусловная) вероятность появления события в
-м опыте оно появилось, больше, чем простая (безусловная) вероятность появления события в  -м опыте
-м опыте  (между появлениями события в
(между появлениями события в 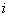 -м и
-м и  -м опытах имеется положительная корреляция). Если это так для любой пары опытов, то поправочный член в формуле (10.3.14) положителен и дисперсия числа появлений события при зависимых опытах больше, чем при независимых.
-м опытах имеется положительная корреляция). Если это так для любой пары опытов, то поправочный член в формуле (10.3.14) положителен и дисперсия числа появлений события при зависимых опытах больше, чем при независимых.
Если вероятность 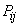 меньше, чем
меньше, чем  (между появлениями события в
(между появлениями события в 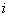 -м и
-м и  -м опытах существует отрицательная корреляция), то соответствующее слагаемое отрицательно. Если это так для любой пары опытов, то дисперсия числа появлений события при зависимых опытах меньше, чем при независимых.
-м опытах существует отрицательная корреляция), то соответствующее слагаемое отрицательно. Если это так для любой пары опытов, то дисперсия числа появлений события при зависимых опытах меньше, чем при независимых.
Рассмотрим частный случай, когда  ,
,  , т. е. условия всех опытов одинаковы. Формула (10.3.14) принимает вид:
, т. е. условия всех опытов одинаковы. Формула (10.3.14) принимает вид:
 , (10.3.15)
, (10.3.15)
где 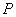 - вероятность появления события
- вероятность появления события  сразу в паре опытов (все равно каких).
сразу в паре опытов (все равно каких).
В этом частном случае особый интерес представляют два подслучая:
1. Появление события  в любом из опытов влечет за собой с достоверностью его появление в каждом из остальных. Тогда
в любом из опытов влечет за собой с достоверностью его появление в каждом из остальных. Тогда 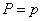 , и формула (10.3.15) принимает вид:
, и формула (10.3.15) принимает вид:
 .
.
2. Появление события  в любом из опытов исключает его появление в каждом из остальных. Тогда
в любом из опытов исключает его появление в каждом из остальных. Тогда  , и формула (10.3.15) принимает вид:
, и формула (10.3.15) принимает вид:
 .
.
Задача 7. Математическое ожидание числа объектов, приведенных в заданное состояние.
На практике часто встречается следующая задача. Имеется некоторая группа, состоящая из  объектов, по которым осуществляется какое-то воздействие. Каждый из объектов в результате воздействия может быть приведен в определенное состояние
объектов, по которым осуществляется какое-то воздействие. Каждый из объектов в результате воздействия может быть приведен в определенное состояние  (например, поражен, исправлен, обнаружен, обезврежен и т. п.). Вероятность того, что
(например, поражен, исправлен, обнаружен, обезврежен и т. п.). Вероятность того, что 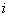 -й объект будет приведен в состояние
-й объект будет приведен в состояние  , равна
, равна  . Найти математическое ожидание числа объектов, которые в результате воздействия по группе будут приведены в состояние
. Найти математическое ожидание числа объектов, которые в результате воздействия по группе будут приведены в состояние  .
.
Решение. Свяжем с каждым из объектов случайную величину  , которая принимает значения
, которая принимает значения  или
или  :
:

Случайная величина  - число объектов, приведенных в состояние
- число объектов, приведенных в состояние  , - может быть представлена в виде суммы:
, - может быть представлена в виде суммы:
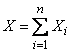 .
.
Отсюда, пользуясь теоремой сложения математических ожиданий, получим:
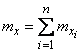 .
.
Математическое ожидание каждой из случайных величин  известно:
известно:
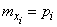 .
.
Следовательно,
 , (10.3.16)
, (10.3.16)
т. Об этом говорит сайт https://intellect.icu . е. математическое ожидание числа объектов, приведенных в состояние  , равно сумме вероятностей перехода в это состояние для каждого из объектов.
, равно сумме вероятностей перехода в это состояние для каждого из объектов.
Особо подчеркнем, что для справедливости доказанной формулы вовсе не нужно, чтобы объекты переходили в состояние  независимо друг от друга. Формула справедлива для любого вида воздействия.
независимо друг от друга. Формула справедлива для любого вида воздействия.
Задача 8. Дисперсия числа объектов, приведенных в заданное состояние.
Если в условиях предыдущей задачи переход каждого из объектов состояние  происходит независимо от всех других, то, применяя теорему сложения дисперсий к величине
происходит независимо от всех других, то, применяя теорему сложения дисперсий к величине
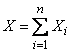 ,
,
получим дисперсию числа объектов, приведенных в состояние  :
:
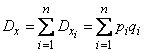 ,
, 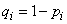 . (10.3.17)
. (10.3.17)
Если же воздействие по объектам производится так, что переходы в состояние  для отдельных объектов зависимы, то дисперсия числа объектов, переведенных в состояние
для отдельных объектов зависимы, то дисперсия числа объектов, переведенных в состояние  , выразится формулой (см. задачу 6)
, выразится формулой (см. задачу 6)
 , (10.3.18)
, (10.3.18)
где 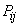 - вероятность того, что в результате воздействия
- вероятность того, что в результате воздействия 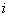 -й и
-й и  -й объекты вместе перейдут в состояние
-й объекты вместе перейдут в состояние  .
.
Задача 9. Математическое ожидание числа опытов до  -го появления события.
-го появления события.
Производится ряд независимых опытов, в каждом из которых может с вероятностью 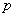 появиться событие
появиться событие  . Опыты проводятся до тех пор, пока событие
. Опыты проводятся до тех пор, пока событие  не появится
не появится  раз, после чего опыты прекращаются. Определить математическое ожидание, дисперсию и с. к. о. числа опытов
раз, после чего опыты прекращаются. Определить математическое ожидание, дисперсию и с. к. о. числа опытов  , которое будет произведено.
, которое будет произведено.
Решение. В примере 3  5.7 были определены математическое ожидание и дисперсия числа опытов до первого появления события
5.7 были определены математическое ожидание и дисперсия числа опытов до первого появления события  :
:
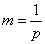 ,
,  ,
,
где 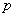 - вероятность появления события в одном опыте,
- вероятность появления события в одном опыте,  - вероятность непоявления.
- вероятность непоявления.
Рассмотрим случайную величину  - число опытов до
- число опытов до  -го появления события
-го появления события  . Ее можно представить в виде суммы:
. Ее можно представить в виде суммы:
 ,
,
где 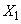 - число опытов до первого появления события
- число опытов до первого появления события  ,
,
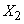 - число опытов от первого до второго появления события
- число опытов от первого до второго появления события  (считая второе),
(считая второе),
………………………………………………………………………………………
 - число опытов от
- число опытов от 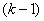 -го до
-го до  -го появления события
-го появления события  (считая
(считая  -е).
-е).
Очевидно, величины  независимы; каждая из них распределена по тому же закону, что и первая из них (число опытов до первого появления события) и имеет числовые характеристики
независимы; каждая из них распределена по тому же закону, что и первая из них (число опытов до первого появления события) и имеет числовые характеристики
 ,
,  .
.
Применяя теоремы сложения математических ожиданий и дисперсий, получим:
 (10.3.19)
(10.3.19)
Задача 10. Средний расход средств до достижения заданного результата.
В предыдущей задаче был рассмотрен случай, когда предпринимается ряд опытов с целью получения вполне определенного результата -  появлений события
появлений события  , которое в каждом опыте имеет одну и ту же вероятность. Эта задача является частным случаем другой, когда производится ряд опытов с целью достижения любого результата
, которое в каждом опыте имеет одну и ту же вероятность. Эта задача является частным случаем другой, когда производится ряд опытов с целью достижения любого результата  , вероятность которого с увеличением числа опытов
, вероятность которого с увеличением числа опытов  возрастает по любому закону
возрастает по любому закону 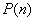 . Предположим, что на каждый опыт расходуется определенное количество средств
. Предположим, что на каждый опыт расходуется определенное количество средств  . Требуется найти математическое ожидание количества средств, которое будет израсходовано.
. Требуется найти математическое ожидание количества средств, которое будет израсходовано.
Решение. Для того чтобы решить задачу, сначала предположим, что число производимых опытов ничем не ограничено, и что они продолжаются и после достижения результата  . Тогда некоторые из этих опытов будут излишними. Условимся называть опыт «необходимым», если он производится при еще не достигнутом результате
. Тогда некоторые из этих опытов будут излишними. Условимся называть опыт «необходимым», если он производится при еще не достигнутом результате  , и «излишним», если он производится при уже достигнутом результате
, и «излишним», если он производится при уже достигнутом результате  .
.
Свяжем с каждым (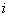 -м) опытом случайную величину
-м) опытом случайную величину  , которая равна нулю или единице в зависимости от того, «необходимым» или «излишним» оказался этот опыт. Положим
, которая равна нулю или единице в зависимости от того, «необходимым» или «излишним» оказался этот опыт. Положим
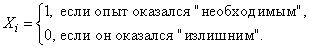
Рассмотрим случайную величину  - число опытов, которое придется произвести для получения результата
- число опытов, которое придется произвести для получения результата  . Очевидно, ее можно представить в виде суммы:
. Очевидно, ее можно представить в виде суммы:
 (10.3.20)
(10.3.20)
Из величин в правой части (10.3.20) первая  является неслучайной и всегда равна единице (первый опыт всегда «необходим»). Каждая из остальных - случайная величина с возможными значениями
является неслучайной и всегда равна единице (первый опыт всегда «необходим»). Каждая из остальных - случайная величина с возможными значениями  и
и  . Построим ряд распределения случайной величины
. Построим ряд распределения случайной величины  . Он имеет вид:
. Он имеет вид:
|
|
|
|
|
|
(10.3.21)
где  - вероятность достижения результата
- вероятность достижения результата  после
после 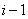 опытов.
опытов.
Действительно, если результат  уже был достигнут при предыдущих
уже был достигнут при предыдущих 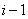 опытах, то
опытах, то  (опыт излишен), если не достигнут, то
(опыт излишен), если не достигнут, то  (опыт необходим).
(опыт необходим).
Найдем математическое ожидание величины  . Из ряда распределения (10.3.21) имеем:
. Из ряда распределения (10.3.21) имеем:
 .
.
Нетрудно убедиться, что та же формула будет справедлива и при  , так как
, так как 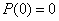 .
.
Применим к выражению (10.3.20) теорему сложения математических ожиданий. Получим:
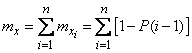
или, обозначая  ,
,
 . (10.3.22)
. (10.3.22)
Каждый опыт требует затраты средств  . Умножая полученную величину
. Умножая полученную величину  на
на  , определим среднюю затрату средств на достижение результата
, определим среднюю затрату средств на достижение результата  :
:
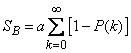 . (10.3.23)
. (10.3.23)
Данная формула выведена в предположении, что стоимость каждого опыта одна и та же. Если это не так, то можно применить другой прием - представить суммарную затрату средств  как сумму затрат на выполнение отдельных опытов, которая принимает два значения:
как сумму затрат на выполнение отдельных опытов, которая принимает два значения: 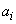 , если
, если 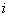 -й опыт «необходим», и нуль, если он «излишен». Средний расход средств
-й опыт «необходим», и нуль, если он «излишен». Средний расход средств  представится в виде:
представится в виде:
 . (10.3.24)
. (10.3.24)
Задача 11. Математическое ожидание суммы случайного числа случайных слагаемых.
В ряде практических приложений теории вероятностей приходится встречаться с суммами случайных величин, в которых число слагаемых заранее неизвестно, случайно.
Поставим следующую задачу. Случайная величина  представляет собой сумму
представляет собой сумму  случайных величин:
случайных величин:
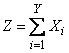 , (10.3.25)
, (10.3.25)
причем  - также случайная величина. Допустим, что нам известны математические ожидания
- также случайная величина. Допустим, что нам известны математические ожидания  всех слагаемых:
всех слагаемых:
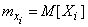
и что величина  не зависит ни от одной из величин
не зависит ни от одной из величин  .
.
Требуется найти математическое ожидание величины  .
.
Решение. Число слагаемых в сумме есть дискретная случайная величина. Предположим, что нам известен ее ряд распределения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где 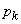 - вероятность того, что величина
- вероятность того, что величина  приняла значение
приняла значение  . Зафиксируем значение
. Зафиксируем значение 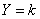 и найдем при этом условии математическое ожидание величины
и найдем при этом условии математическое ожидание величины  (условное математическое ожидание):
(условное математическое ожидание):
 . (10.3.26)
. (10.3.26)
Теперь применим формулу полного математического ожидания, для чего умножим каждое условное математическое ожидание на вероятность соответствующей гипотезы 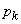 и сложим:
и сложим:
 . (10.3.27)
. (10.3.27)
Особый интерес представляет случай, когда все случайные величины 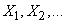 имеют одно и то же математическое ожидание:
имеют одно и то же математическое ожидание:
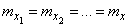 .
.
Тогда формула (10.3.26) принимает вид:
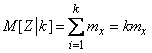
и
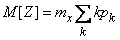 . (10.3.28)
. (10.3.28)
Сумма в выражении (10.3.28) представляет собой не что иное, как математическое ожидание величины  :
:
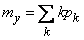 .
.
Отсюда
 , (10.3.29)
, (10.3.29)
т. е. математическое ожидание суммы случайного числа случайных слагаемых с одинаковыми средними значениями (если только число слагаемых не зависит от их значений) равно произведению среднего значения каждого из слагаемых на среднее число слагаемых.
Снова отметим, что полученный результат справедлив как для независимых, так и для зависимых слагаемых  лишь бы число слагаемых
лишь бы число слагаемых  не зависело от самих слагаемых.
не зависело от самих слагаемых.
Ниже мы решим ряд конкретных примеров из разных областей практики, на которых продемонстрируем конкретное применение общих методов оперирования с числовыми характеристиками, вытекающих из доказанных теорем, и специфических приемов, связанных с решенными выше общими задачами.
Пример 1. Монета бросается 10 раз. Определить математическое ожидание и среднее квадратическое отклонение числа  выпавших гербов.
выпавших гербов.
Решение. По формулам (10.3.7) и (10.3.10) найдем:
 ;
; 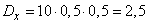 ;
;  .
.
Пример 2. Производится 5 независимых выстрелов по круглой мишени диаметром 20 см. Прицеливание - по центру мишени, систематическая ошибка отсутствует, рассеивание - круговое, среднее квадратическое отклонение 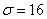 см. Найти математическое ожидание и с. к. о. числа попаданий.
см. Найти математическое ожидание и с. к. о. числа попаданий.
Решение. Вероятность попадания в мишень при одном выстреле вычислим по формуле (9.4.5):
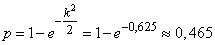 .
.
Пользуясь формулами (10.3.7) и (10.3.10), получим:
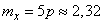 ;
;  ;
;  .
.
Пример 3. Производится отражение воздушного налета, в котором участвует 20 летательных аппаратов типа 1 и 30 летательных аппаратом типа 2. Летательные аппараты типа 1 атакуются истребительной авиацией. Число атак, приходящееся на каждый аппарат, подчинено закону Пуассона с параметром 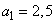 . Каждой атакой истребителя летательный аппарат типа 1 поражается с вероятностью
. Каждой атакой истребителя летательный аппарат типа 1 поражается с вероятностью  . Летательные аппараты типа 2 атакуются зенитными управляемыми ракетами. Число ракет, направляемых на каждый аппарат, подчинено закону Пуассона с параметром
. Летательные аппараты типа 2 атакуются зенитными управляемыми ракетами. Число ракет, направляемых на каждый аппарат, подчинено закону Пуассона с параметром  , каждая ракета поражает летательный аппарат типа 2 с вероятностью
, каждая ракета поражает летательный аппарат типа 2 с вероятностью  . Все аппараты, входящие в состав налета, атакуются и поражаются независимо друг от друга. Найти:
. Все аппараты, входящие в состав налета, атакуются и поражаются независимо друг от друга. Найти:
1) математическое ожидание, дисперсию и с. к. о. числа пораженных летательных аппаратов типа 1;
2) математическое ожидание, дисперсию и с. к. о. числа пораженных летательных аппаратов типа 2;
3) математическое ожидание, дисперсию и с. к. о. числа пораженных летательных аппаратов обоих типов.
Решение. Рассмотрим вместо «числа атак» на каждый аппарат типа 1 «число поражающих атак», тоже распределенное по закону Пуассона, но с другим параметром:
 .
.
Вероятность поражения каждого из летательных аппаратов типа 1 будет равна вероятности того, что на него придется хотя бы одна поражающая атака:
 .
.
Вероятность поражения каждого из летательных аппаратов типа 2 найдем аналогично:
 .
.
Математическое ожидание числа пораженных аппаратов типа 1 будет:
 .
.
Дисперсия и с. к. о. этого числа:
 ,
, 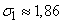 .
.
Математическое ожидание, дисперсия числа и с. к. о. пораженных аппаратов типа 2:
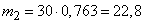 ,
, 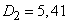 ,
,  .
.
Математическое ожидание, дисперсия и с. к. о. общего числа пораженных аппаратов обоих типов:
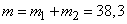 ,
,  ,
,  .
.
Пpимер 4. Случайные величины  и
и  представляют собой элементарные ошибки, возникающие на входе прибора. Они имеют математические ожидания
представляют собой элементарные ошибки, возникающие на входе прибора. Они имеют математические ожидания 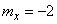 и
и  , дисперсии
, дисперсии  и
и  ; коэффициент корреляции этих ошибок равен
; коэффициент корреляции этих ошибок равен 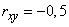 . Ошибка на выходе прибора связана с ошибками на входе функциональной зависимостью:
. Ошибка на выходе прибора связана с ошибками на входе функциональной зависимостью:
 .
.
Найти математическое ожидание ошибки на выходе прибора.
Решение.
 .
.
Пользуясь связью между начальными и центральными моментами и формулой (10.2.17), имеем:
 ;
;
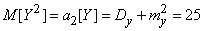 ;
;
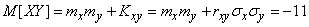 ,
,
откуда
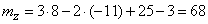 .
.
Пример 5. Самолет производит бомбометание по автостраде, ширина которой 30 м (рис. 10.3.2). Направление полета составляет угол  с направлением автострады. Прицеливание - по средней линии автострады, систематические ошибки отсутствуют. Рассеивание задано главными вероятными отклонениями: по направлению полета
с направлением автострады. Прицеливание - по средней линии автострады, систематические ошибки отсутствуют. Рассеивание задано главными вероятными отклонениями: по направлению полета  м и в боковом направлении
м и в боковом направлении  м. Найти вероятность попадания в автостраду при сбрасывании одной бомбы.
м. Найти вероятность попадания в автостраду при сбрасывании одной бомбы.

Рис. 10.3.2
Решение. Спроектируем случайную точку попадания на ось  перпендикулярную к автостраде и применим формулу (10.3.3). Она, очевидно, остается справедливой, если в нее вместо средних квадратических подставить вероятные отклонения:
перпендикулярную к автостраде и применим формулу (10.3.3). Она, очевидно, остается справедливой, если в нее вместо средних квадратических подставить вероятные отклонения:
 .
.
Отсюда
 ,
, 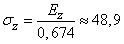 .
.
Вероятность попадания в автостраду найдем по формуле (6.3.10):
 .
.
Примечание. Примененный здесь прием пересчета рассеивания к другим осям пригоден только для вычисления вероятности попадания в область, имеющую вид полосы; для прямоугольника, стороны которого повернуты под углом к осям рассеивания, он уже не годится. Вероятность попадания в каждую из полос, пересечением которых образован прямоугольник, может быть вычислена с помощью этого приема, однако вероятность попадания в прямоугольник уже не равна произведению вероятностей попадания в полосы, так как эти события зависимы.
Пример 6. Производится наблюдение с помощью системы радиолокационных станций за группой объектов в течение некоторого времени; группа состоит из четырех объектов; каждый из них за время 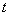 обнаруживается с вероятностью, равной соответственно:
обнаруживается с вероятностью, равной соответственно:
 ,
,  ,
,  ,
,  .
.
Найти математическое ожидание числа объектов, которые будут обнаружены через время 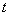 .
.
Решение. По формуле (10.3.16) имеем:
 .
.
Пример 7. Предпринимается ряд мероприятий, каждое из которых если оно состоится, приносит случайный чистый доход  , распределенный по нормальному закону со средним значением
, распределенный по нормальному закону со средним значением 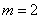 (условных единиц). Число мероприятий за данный период времени случайно и распределено по закону
(условных единиц). Число мероприятий за данный период времени случайно и распределено по закону
|
|
|
|
|
|
|
|
|
|
|
|
причем не зависит от доходов, приносимых мероприятиями. Определить средний ожидаемый доход за весь период.
Решение. На основе задачи 11 данного  находим математическое ожидание полного дохода
находим математическое ожидание полного дохода  :
:
 ,
,
где  - средний доход от одного мероприятия,
- средний доход от одного мероприятия,  - среднее ожидаемое число мероприятий. Имеем:
- среднее ожидаемое число мероприятий. Имеем:
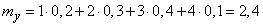 ,
,
 ,
,
 .
.
Пример 8. Ошибка прибора выражается функцией
 , (10.3.30)
, (10.3.30)
где  - так называемые «первичные ошибки», представляющие собой систему случайных величин (случайный вектор).
- так называемые «первичные ошибки», представляющие собой систему случайных величин (случайный вектор).
Случайный вектор 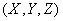 характеризуется математическими ожиданиями
характеризуется математическими ожиданиями
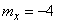 ;
;  ;
; 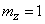
и корреляционной матрицей:
 .
.
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение ошибки прибора.
Решение. Так как функция (10.3.30) линейна, применяя формулы (10.2.6) и (10.2.13), находим:
 ,
,
 ,
,
 .
.
Пример 9. Для обнаружения источника неисправности в вычислительной машине проводятся пробы (тесты). В каждой пробе неисправность независимо от других проб локализуется с вероятностью  . На каждую пробу в среднем уходит 3 минуты. Найти математическое ожидание времени, которое потребуется для локализации неисправности.
. На каждую пробу в среднем уходит 3 минуты. Найти математическое ожидание времени, которое потребуется для локализации неисправности.
Решение. Пользуясь результатом задачи 9 данного  (математическое ожтдание числа опытов до
(математическое ожтдание числа опытов до  -го появления события
-го появления события  ), полагая
), полагая  , найдем среднее число проб
, найдем среднее число проб
 .
.
На эти пять проб потребуется в среднем
 (минут).
(минут).
Пример 10. Производится стрельба по резервуару с горючим. Вероятность попадания при каждом выстреле равна 0,3. Выстрелы независимы. При первом попадании в резервуар появляется только течь горючего, при втором попадании горючее воспламеняется. После воспламенения горючего стрельба прекращается. Найти математическое ожидание числа произведенных выстрелов.
Решение. Пользуясь той же формулой, что и в предыдущем примере, найдем математическое ожидание числа выстрелов до 2-го попадания:
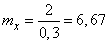 .
.
Пример 11. Вероятность обнаружения объекта радиолокатором с ростом числа циклов обзора растет по закону:
 ,
,
где  - число циклов, начиная с начала наблюдения.
- число циклов, начиная с начала наблюдения.
Найти математическое ожидание числа циклов, после которого объект будет обнаружен.
Решение. Пользуясь результатами задачи 10 данного параграфа получим:
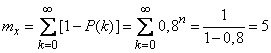 .
.
Пример 12. Для того чтобы выполнить определенную задачу по сбору информации, в заданный район высылается несколько разведчиков. Каждый посланный разведчик достигает района назначения с вероятностью 0,7. Для выполнения задачи достаточно наличия в районе трех разведчиков. Один разведчик с задачей вообще справиться не может, а два разведчика выполняют ее с вероятностью 0,4. Обеспечена непрерывная связь с районом, и дополнительные разведчики посылаются, только если задача еще не выполнена.
Требуется найти математическое ожидание числа разведчиков, которые будут посланы.
Решение. Обозначим  - число прибывших в район разведчиков, которое оказалось достаточным для выполнения задачи. В задаче 10 данного
- число прибывших в район разведчиков, которое оказалось достаточным для выполнения задачи. В задаче 10 данного  было найдено математическое ожидание числа опытов, которое нужно для того, чтобы достигнуть определенного результата, вероятность которого с увеличением числа опытов возрастает по закону
было найдено математическое ожидание числа опытов, которое нужно для того, чтобы достигнуть определенного результата, вероятность которого с увеличением числа опытов возрастает по закону 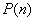 . Это математическое ожидание равно:
. Это математическое ожидание равно:
 .
.
В нашем случае:
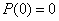 ;
; 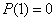 ;
;  ;
; 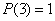 ;
;
 .
.
Математическое ожидание величины  равно:
равно:
 .
.
Итак, для того чтобы задача была выполнена, необходимо, чтобы в район прибыло в среднем 2,6 разведчика.
Теперь решим следующую задачу. Сколько разведчиков придется в среднем выслать в район для того, чтобы их в среднем прибыло  ?
?
Пусть послано  разведчиков. Число прибывших разведчиков можно представить в виде
разведчиков. Число прибывших разведчиков можно представить в виде
 ,
,
где случайная величина  принимает значение 1, если
принимает значение 1, если 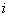 -й разведчик прибыл, и 0, если не прибыл. Величина
-й разведчик прибыл, и 0, если не прибыл. Величина  есть не что иное, как сумма случайного числа случайных слагаемых (см. задачу 11 данного
есть не что иное, как сумма случайного числа случайных слагаемых (см. задачу 11 данного  ). С учетом этого имеем:
). С учетом этого имеем:
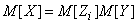 ,
,
откуда
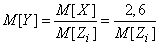 ,
,
но  , где
, где 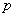 - вероятность прибытия отправленного разведчика (в нашем случае
- вероятность прибытия отправленного разведчика (в нашем случае  ). Величина
). Величина  нами только что найдена и равна 2.6 Имеем:
нами только что найдена и равна 2.6 Имеем:
 .
.
Пример 13. Радиолокационная станция просматривает область пространства, в которой находится 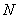 объектов. За один цикл обзора она обнаруживает каждый из объектов (независимо от других циклов) с вероятностью
объектов. За один цикл обзора она обнаруживает каждый из объектов (независимо от других циклов) с вероятностью 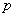 . На один цикл требуется время
. На один цикл требуется время  . Сколько времени потребуете на то, чтобы из
. Сколько времени потребуете на то, чтобы из 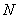 объектов обнаружить в среднем
объектов обнаружить в среднем  ?
?
Решение. Найдем прежде всего математическое ожидание числа обнаруженных объектов после  циклов обзора. За
циклов обзора. За  циклов один (любой) из объектов обнаруживается с вероятностью
циклов один (любой) из объектов обнаруживается с вероятностью
 ,
,
а среднее число объектов, обнаруженных за  циклов, по теореме сложения математических ожиданий (см. задачу 5 данного
циклов, по теореме сложения математических ожиданий (см. задачу 5 данного  ) равно:
) равно:
 .
.
Полагая
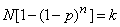 ,
,
получим необходимое число циклов  из уравнения
из уравнения
 ,
,
решая которое, найдем:
 ,
,
откуда время, необходимое для обнаружения в среднем  объектов, будет равно:
объектов, будет равно:
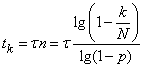 .
.
Пример 14. Изменим условия примера 13. Пусть радиолокационная станция ведет наблюдение за областью только до тех пор, пока не будет обнаружено  объектов, после чего наблюдение прекращается или продолжается в новом режиме. Найти математическое ожидание времени, которое для этого понадобится.
объектов, после чего наблюдение прекращается или продолжается в новом режиме. Найти математическое ожидание времени, которое для этого понадобится.
Для того чтобы решить эту задачу, недостаточно задаться вероятностью обнаружения одного объекта в одном цикле, а надо еще указать, как растет с увеличением числа циклов вероятность того, что из 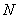 объектов будет обнаружено не менее
объектов будет обнаружено не менее  . Проще всего вычислить эту вероятность, если предположить, что объекты обнаруживаются независимо друг от друга. Сделаем такое допущение и решим задачу.
. Проще всего вычислить эту вероятность, если предположить, что объекты обнаруживаются независимо друг от друга. Сделаем такое допущение и решим задачу.
Решение. При независимых обнаружениях можно наблюдение за 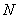 объектами представить как
объектами представить как 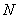 независимых опытов. После
независимых опытов. После  циклов каждый из объектов обнаруживается с вероятностью
циклов каждый из объектов обнаруживается с вероятностью
 .
.
Вероятность того, что после  циклов будет обнаружено не менее
циклов будет обнаружено не менее  объектов из
объектов из 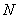 , найдем по теореме о повторении опытов:
, найдем по теореме о повторении опытов:
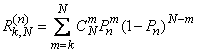 .
.
Среднее число циклов, после которых будет обнаружено не менее  объектов, определится по формуле (10.3.22):
объектов, определится по формуле (10.3.22):
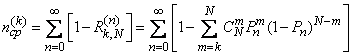 .
.
Пример 15. На плоскости  случайная точка
случайная точка  с координации
с координации  отклоняется от требуемого положения (начало координат) под влиянием трех независимых векторных ошибок
отклоняется от требуемого положения (начало координат) под влиянием трех независимых векторных ошибок  ,
, 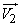 и
и  . Каждый из векторов характеризуется двумя составляющими:
. Каждый из векторов характеризуется двумя составляющими:
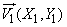 ,
, 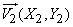 ,
, 
(рис. 10.3.3). Числовые характеристики этих трех векторов равны:
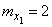 ,
,  ,
,  ,
,  ,
, 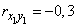 ,
,
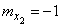 ,
, 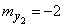 ,
,  ,
, 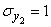 ,
, 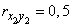 ,
,
 ,
,  ,
,  ,
,  ,
,  .
.

Рис. 10.3.3
Найти характеристики суммарной ошибки (вектора, отклоняющего точку  от начала координат).
от начала координат).
Решение. Применяя теоремы сложения математических ожиданий, дисперсий и корреляционных моментов, получим:
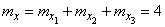 ,
,
 ,
,
 ,
, 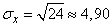 ,
,
 ,
, 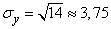 ,
,
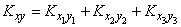 ,
,
где
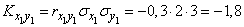 ,
,
 ,
,
 ,
,
откуда

и
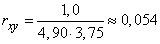 .
.
Пример 16. Тело, которое имеет форму прямоугольного параллелепипеда с размерами  летит в пространстве, беспорядочно вращаясь вокруг центра массы так, что все его ориентации одинаково вероятны. Тело находится в потоке частиц, и среднее число частиц, встречающихся с телом, пропорционально средней площади, которую тело подставляет потоку. Найти математическое ожидание площади проекции тела на плоскость, перпендикулярную направлению его движения.
летит в пространстве, беспорядочно вращаясь вокруг центра массы так, что все его ориентации одинаково вероятны. Тело находится в потоке частиц, и среднее число частиц, встречающихся с телом, пропорционально средней площади, которую тело подставляет потоку. Найти математическое ожидание площади проекции тела на плоскость, перпендикулярную направлению его движения.
Решение. Так как все ориентации тела в пространстве одинаково вероятны, то направление плоскости проекций безразлично. Очевидно, площадь проекции тела равна половине суммы проекций всех граней параллелепипеда (так как каждая точка проекции представляет собой проекцию двух точек на поверхности тела). Применяя теорему сложения математических ожиданий и формулу для средней площади проекции плоской фигуры (см. пример 3  10.1), получим:
10.1), получим:
 ,
,
где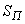 - полная площадь поверхности параллелепипеда.
- полная площадь поверхности параллелепипеда.
Заметим, что выведенная формула справедлива не только для параллелепипеда, но и для любого выпуклого тела: средняя площадь проекции такого тела при беспорядочном вращении равна одной четверти полной его поверхности. Рекомендуем читателю в качестве упражнения доказать это положение.
Пример 17. На оси абсцисс  движется случайным образом точка
движется случайным образом точка  по следующему закону. В начальный момент она находится в начале координат и начинает двигаться с вероятностью
по следующему закону. В начальный момент она находится в начале координат и начинает двигаться с вероятностью 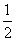 вправо и с вероятностью
вправо и с вероятностью 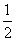 влево. Пройдя единичное расстояние, точка с вероятностью
влево. Пройдя единичное расстояние, точка с вероятностью 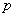 продолжает двигаться в том же направлении, а с вероятностью
продолжает двигаться в том же направлении, а с вероятностью  меняет его на противоположное. Пройдя единичное расстояние, точка снова с вероятностью
меняет его на противоположное. Пройдя единичное расстояние, точка снова с вероятностью 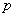 продолжает движение в том направлении, в котором двигалась, а с вероятностью
продолжает движение в том направлении, в котором двигалась, а с вероятностью  меняет его на противоположное и т. д.
меняет его на противоположное и т. д.
В результате такого случайного блуждания по оси абсцисс точка  после
после  шагов займет случайное положение, которое мы обозначим
шагов займет случайное положение, которое мы обозначим 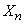 . Требуется найти характеристики случайной величины
. Требуется найти характеристики случайной величины 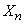 : математическое ожидание и дисперсию.
: математическое ожидание и дисперсию.
Решение. Прежде всего, из соображений симметрии задачи ясно, что 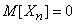 . Чтобы найти
. Чтобы найти  , представим
, представим 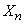 в виде суммы
в виде суммы  слагаемых:
слагаемых:
 , (10.3.31)
, (10.3.31)
где 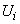 - расстояние, пройденное точкой на
- расстояние, пройденное точкой на 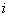 -м шаге, т. е.
-м шаге, т. е. 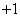 , если точка двигалась на этом шаге вправо, и
, если точка двигалась на этом шаге вправо, и  , если она двигалась влево.
, если она двигалась влево.
По теореме о дисперсии суммы (см. формулу (10.2.10)) имеем:
 .
.
Ясно, что 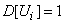 , так как величина
, так как величина 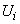 принимает значения
принимает значения 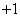 и
и  с одинаковой вероятностью (из тех же соображений симметрии). Найдем корреляционные моменты
с одинаковой вероятностью (из тех же соображений симметрии). Найдем корреляционные моменты
 .
.
Начнем со случая  , когда величины
, когда величины 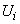 и
и 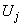 стоят рядом в сумме (10.3.31). Ясно, что
стоят рядом в сумме (10.3.31). Ясно, что  принимает значение
принимает значение 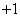 с вероятностью
с вероятностью 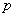 и значение
и значение  с вероятностью
с вероятностью  . Имеем:
. Имеем:
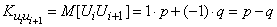 .
.
Рассмотрим, далее, случай  . В этом случае произведение
. В этом случае произведение  равно
равно 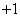 , если оба перемещения - на
, если оба перемещения - на 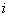 -м и
-м и  -м шаге - происходят в одном и том же направлении. Это может произойти двумя способами. Или точка
-м шаге - происходят в одном и том же направлении. Это может произойти двумя способами. Или точка  все три шага -
все три шага - 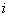 -й,
-й,  -й и
-й и  -й - двигалась в одном и том же направлении, или же она дважды изменила за эти три шага свое направление. Найдем вероятность того, что
-й - двигалась в одном и том же направлении, или же она дважды изменила за эти три шага свое направление. Найдем вероятность того, что 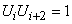 :
:

 .
.
Найдем теперь вероятность того, что 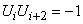 . Это тоже может произойти двумя способами: или точка изменила свое направление при переводе от
. Это тоже может произойти двумя способами: или точка изменила свое направление при переводе от 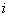 -го шага к
-го шага к  -му, а при переходе от
-му, а при переходе от  -го шага к
-го шага к  -му сохранила его, или наоборот. Имеем:
-му сохранила его, или наоборот. Имеем:
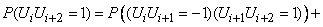
 .
.
Таким образом, величина  имеет два возможных значения
имеет два возможных значения 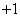 и
и  , которые она принимает с вероятностями соответственно
, которые она принимает с вероятностями соответственно  и
и 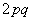 .
.
Ее математическое ожидание равно:
 .
.
Легко доказать по индукции, что для любого расстояния  между шагами в ряду
между шагами в ряду 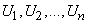 справедливы формулы:
справедливы формулы:
 ,
,
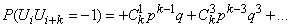 ,
,
и, следовательно,
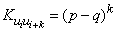 .
.
Таким образом, корреляционная матрица системы случайных величин 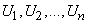 будет иметь вид:
будет иметь вид:
 .
.
Дисперсия случайной величины 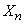 будет равна:
будет равна:
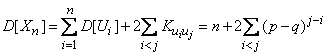 ,
,
или же, производя суммирование элементов, стоящих на одном расстоянии от главной диагонали,
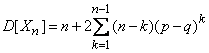 .
.
Пример 18. Найти асимметрию биномиального распределения

 . (10.3.32)
. (10.3.32)
Решение. Известно, что биномиальное распределение (10.3.32) представляет собой распределение числа появлений в  независимых опытах некоторого события, которое в одном опыте имеет вероятность
независимых опытах некоторого события, которое в одном опыте имеет вероятность 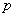 . Представим случайную величину
. Представим случайную величину  - число появлений события в
- число появлений события в  опытах - как сумму
опытах - как сумму  случайных величин:
случайных величин:
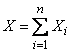 ,
,
где

По теореме сложения третьих центральных моментов
 . (10.3.33)
. (10.3.33)
Найдем третий центральный момент случайной величины  . Она имеет распределения
. Она имеет распределения
|
|
|
|
|
|
Третий центральный момент величины  равен:
равен:
 .
.
Подставляя в (10.3.33), получим:
 .
.
Чтобы получить асимметрию, нужно разделить третий центральный момент величины  на куб среднего квадратического отклонения:
на куб среднего квадратического отклонения:
 .
.
Пример 19. Имеется  положительных, одинаково распределенных независимых случайных величин:
положительных, одинаково распределенных независимых случайных величин:
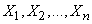 .
.
Найти математическое ожидание случайной величины
 .
.
Решение. Ясно, что математическое ожидание величины  существует, так как она заключена между нулем и единицей. Кроме того, легко видеть, что закон распределения системы величин
существует, так как она заключена между нулем и единицей. Кроме того, легко видеть, что закон распределения системы величин  , каков бы он ни был, симметричен относительно своих переменных, т. е. не меняется при любой их перестановке. Рассмотрим случайные величины:
, каков бы он ни был, симметричен относительно своих переменных, т. е. не меняется при любой их перестановке. Рассмотрим случайные величины:
 ,
,  ,
,  ,
,  .
.
Очевидно, их закон распределения тоже должен обладать свойством симметрии, т. е. не меняться при замене одного аргумента любым другим и наоборот. Отсюда, в частности, вытекает, что
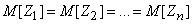 .
.
Вместе с тем нам известно, что в сумме случайные величины  образуют единицу, следовательно, по теореме сложения математических ожиданий,
образуют единицу, следовательно, по теореме сложения математических ожиданий,
 ,
,
откуда
 .
.
Информация, изложенная в данной статье про применения теорем о числовых характеристиках , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое применения теорем о числовых характеристиках и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ