Привет, Вы узнаете о том , что такое собеседование по теории вероятностей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
собеседование по теории вероятностей, тесты по теории вероятности , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ . Кликните на вариант (или варианты ответов), если он правильный - то будет подсвечен зеленым цветом
и вам будет зачислено пару монеток, а если неверный - то красным и будет снята монетка. Удачи в прохождении онлайн теста!
В теории вероятности скрыто множество загадок и вопросов, которые играют важную роль не только в математике, но и в реальном мире. Эта дисциплина предоставляет инструменты для анализа случайных событий и предсказания их вероятностей. Понимание основ вероятности имеет большое значение для принятия обоснованных решений в различных областях, будь то научные исследования, экономические анализы или повседневные решения.
Подготовка к экзаменам и собеседованиям по теории вероятности включает в себя не только понимание базовых концепций, но и способность применять их для решения разнообразных задач. В данной подготовке вопросы и тесты с ответами играют ключевую роль, помогая учащимся и кандидатам оценить свои знания и подготовленность. В этом обзоре мы рассмотрим различные вопросы по теории вероятности, предоставив подробные и понятные ответы, чтобы помочь вам успешно подготовиться к экзаменам и собеседованиям, глубже поняв мир случайностей и вероятностей.
Вероятность составляет основу многих важных концепций науки о данных, от статистических выводов до байесовских сетей. Было бы неправильно сказать, что путь к овладению статистикой начинается с вероятности. Этот тест был проведен, чтобы помочь вам определить свой уровень навыков с вероятностью.
Тест был разработан для проверки концептуальных знаний о вероятности. Если вы один из тех, кто пропустил этот тест, вот вопросы и решения. Вы пропустили тест в реальном времени, но можете прочитать эту статью, чтобы узнать, как вы могли ответить правильно.
Инструкция для прохождения теста по теории вероятности на собеседовании:
Шаг 1: Подготовка
1.1 Изучите основные понятия: Перед собеседованием повторите основные понятия и определения в теории вероятности, такие как события, вероятность, случайные величины и т.д.
1.2 Просмотрите формулы: Ознакомьтесь с основными формулами и методами решения задач по теории вероятности.
1.3 Практикуйтесь: Решайте разнообразные задачи и упражнения по теории вероятности, чтобы укрепить свои навыки и уверенность.
Шаг 2: Во время теста
2.1 Внимательно читайте вопросы: Внимательно читайте каждый вопрос перед тем, как приступить к решению. Понимание условия задачи очень важно для правильного ответа.
2.2 Используйте логику: Применяйте логический подход при решении задач. Выявите, какие известные правила и методы применимы для решения данной задачи.
2.3 Проанализируйте варианты ответов: При выборе ответа обратите внимание на остальные варианты и исключите те, которые очевидно неправильные.
2.4 При необходимости, рисуйте схемы: В сложных задачах по теории вероятности может помочь визуализация. Рисуйте блок-схемы, деревья вероятностей или другие диаграммы, чтобы лучше понять процесс решения.
2.5 Остерегайтесь ловушек: Некоторые вопросы могут быть построены так, чтобы сбить с толку или проверить вашу внимательность. Будьте осторожны и внимательны.
Шаг 3: Не торопитесь
3.1 Уделите каждому вопросу достаточно времени: Не торопитесь, но и не застревайте слишком долго на одном вопросе. Оставьте сложные задачи на потом, если нужно.
3.2 Проверьте свои ответы: Если у вас есть время в конце теста, пройдите по всем вопросам еще раз и проверьте свои ответы.
Шаг 4: После теста
4.1 Анализ результатов: После прохождения теста оцените свои результаты. Изучите задачи, в которых совершили ошибки, чтобы понять, как можно улучшить свои знания в теории вероятности.
4.2 Учите на ошибках: Используйте ошибки, сделанные во время теста, как уроки для улучшения своих навыков и знаний.
Следуя этой инструкции, вы повысите свои шансы успешно пройти тест по теории вероятности на собеседовании. Удачи!
Общие баллы
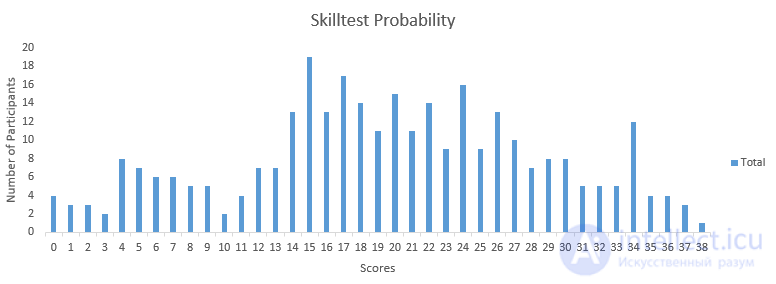
Ниже приведены оценки тех кто уже ответил на эти вопросы, они помогут вам оценить ваши знания .
1. Пусть A и B - события в одном и том же пространстве выборки, с P (A) = 0,6 и P (B) = 0,7. Могут ли эти два события не пересекаться?
Решение: (b)
Эти два события не могут быть несовместимыми, поскольку P (A) + P (B)> 1.
P (AꓴB) = P (A) + P (B) -P (AꓵB).
Событие не пересекается, если P (AꓵB) = 0. Если A и B не пересекаются, P (AꓴB) = 0,6 + 0,7 = 1,3
И поскольку вероятность не может быть больше 1, эти два упомянутых события не могут быть разделены.
2. У Алисы двое детей, одна из которых девочка. Какова вероятность того, что второй ребенок тоже девочка? Вы можете предположить, что в мире равное количество мужчин и женщин.
- a) 0,5
- b) 0,25
- c) 0,333 *
- d) 0,75
Решение: (c)
Результаты для двух детей могут быть {BB, BG, GB, GG}
Поскольку упоминается, что одна из них - девушка, мы можем удалить вариант BB из области выборки. Таким образом, у пробного пространства есть 3 варианта, и только один соответствует второму условию. Следовательно, вероятность того, что вторым ребенком будет девочка, также равна 1/3.
3. Хороший шестигранный кубик бросается дважды. Какова вероятность получить 2 при первом броске и не получить 4 при втором?
- a) 1/36
- b) 1/18
- c) 5/36 *
- d) 1/6
- e) 1/3
Решение: (C)
Два упомянутых события независимы. Первый бросок кубика не зависит от второго броска. Следовательно, вероятности можно напрямую умножать.
P (получение первых 2) = 1/6
P (без второй 4) = 5/6
Следовательно, P (получение первых 2 и отсутствия вторых 4) = 1/6 * 5/6 = 5/36
4.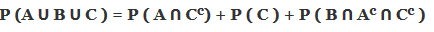
Решение: (A)
P (AꓵCc) будет только P (A). P (только A) + P (C) сделает его P (AꓴC). P (BꓵAcꓵCc) равно P (только B), поэтому P (AꓴC) и P (только B) образуют P (AꓴBꓴC)
5. Возьмите четырехгранный кубик и бросьте его дважды. Какова вероятность того, что число в первом броске строго больше числа во втором? Примечание: четырехгранная матрица имеет только четыре стороны (1, 2, 3 и 4..
- a) 1/2
- b) 3/8 *
- c) 16/7
- d) 16 сентября
Решение: (B)
| (1,1) |
(2,1) |
(3,1) |
(4,1) |
| (1,2) |
(2,2) |
(3,2) |
(4,2) |
| (1,3) |
(2,3) |
(3,3) |
(4,3) |
| (1,4. |
(2,4. |
(3,4) |
(4,4) |
Есть 6 из 16 возможных вариантов, когда первый результат строго выше второго.
6. Какой из следующих вариантов не может быть вероятностью какого-либо события? A) -0,00001 B) 0,5 C) 1,001
- a) Только А
- b) Только Б
- c) Только C
- d) А и Б
- e) B и C
- f) A и C *
Решение: (F)
Вероятность всегда находится в пределах от 0 до 1.
7. Анита случайным образом выбирает 4 карты из колоды из 52 карт и кладет их обратно в колоду (любой набор из 4 карт одинаково вероятен). Затем Бабита случайным образом выбирает 8 карт из одной колоды (любой набор из 8 карт одинаково вероятен). Предположим, что выбор 4 карт Анитой и выбор 8 карт Бабитой независимы. Какова вероятность того, что все 4 карты, выбранные Анитой, входят в набор из 8 карт, выбранных Бабитой?
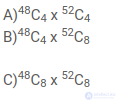
- a)
- b)
- c)
- d) Ничего из вышеперечисленного
Решение: (A)
Общее количество возможных комбинаций будет 52 C 4 (Для выбора 4 карт Анитой) * 52 C 8 (Для выбора 8 карт Бабитой).
Поскольку 4 карты, которые выбирает Анита, входят в число 8 карт, которые выбрала Бабита, таким образом, количество возможных комбинаций составляет 52 C 4 (для выбора 4 карт, выбранных Анитой) * 48 C 4 (Для выбора любых других 4 карт с помощью Бабита, так как 4 карты, выбранные Анитой, обычные)
8. Если вы раздали 13 карт, какова вероятность того, что 13-я карта - король? Контекст вопроса 8:Игроку случайным образом раздается последовательность из 13 карт из колоды из 52 карт. Все последовательности из 13 карт равновероятны. В эквивалентной модели карты выбираются и раздаются по одной. При выборе карты дилер с равной вероятностью выберет любую из карт, оставшихся в колоде.
- a) 1/52
- b) 1/13 *
- c) 1/26
- d) 1/12
Решение: (B)
Поскольку нам ничего не сообщают о первых 12 сданных картах, вероятность того, что 13-я сданная карта является королем, равна вероятности того, что первая сданная карта или фактически любая конкретная сданная карта является королем, и это равно: 4/52
9. Хороший шестигранный кубик бросается 6 раз. Какова вероятность того, что все результаты будут уникальными?
- a) 0,01543 *
- b) 0,01993
- c) 0,23148
- d) 0,03333
Решение: (A)
Чтобы все результаты были уникальными, у нас есть 6 вариантов для первого хода, 5 для второго хода, 4 для третьего хода и так далее.
На первый бросок ограничений нет. На кубике может быть любое из 6 равновероятных значений. Таким образом, вероятность того, что после первого броска не будет дублироваться никаких чисел, равна 6/6, или100%.
При каждом последующем броске количество «успешных» бросков уменьшается на 1. Например, если наш первый бросок был  , то второй бросок должен быть каким угодно, только не
, то второй бросок должен быть каким угодно, только не  , что означает, что для броска 2 существует 5 «успешных» исходов (из 6 возможных). Итак, поскольку каждый бросок не зависит от предыдущих бросков, мы перемножаем их вероятности «успеха». Вероятность того, что после двух бросков не выпадет ни одного повтора, равна 6/6×5/6=5/6, тоесть с вероятностью 83,3%.
, что означает, что для броска 2 существует 5 «успешных» исходов (из 6 возможных). Итак, поскольку каждый бросок не зависит от предыдущих бросков, мы перемножаем их вероятности «успеха». Вероятность того, что после двух бросков не выпадет ни одного повтора, равна 6/6×5/6=5/6, тоесть с вероятностью 83,3%.
Продолжая эту схему, третий бросок будет иметь 4 «успешных» результата из 6, поэтому мы получаем
3 уникальных значения=6/6×5/6×4/6=55,6%
а потом
4 уникальных значения=6/6×5/6×4/6×3/6=27,8%
5 уникальных значений=6/6×5/6×4/6×3/6×2/6=9.26%
и наконец
6 уникальных значений=6×5×4×3×2×1/66 = 0,01543 = 1,54%.
Следовательно, вероятность получения всех уникальных результатов будет равна 0,01543.
10. Группа из 60 студентов случайным образом делится на 3 класса равного размера. Все перегородки одинаково вероятны. Джек и Джилл - два ученика, принадлежащие к этой группе. Какова вероятность того, что Джек и Джилл попадут в один класс?
- a) 1/3
- b) 19/59 *
- c) 18/58
- d) 1/2
Решение: (B)
Присвойте каждому ученику разные номера от 1 до 60. Номера от 1 до 20 относятся к группе 1, от 21 до 40 - к группе 2, от 41 до 60 - к группе 3.
Все возможные разбиения получаются с равной вероятностью путем случайного присвоения этих чисел, не имеет значения, с каких учеников мы начинаем, поэтому мы можем начать с присвоения случайного числа Джеку, а затем мы присваиваем случайное число Джилл. После того, как Джеку было присвоено случайное число, для Джилл доступны 59 случайных чисел, и 19 из них поместят ее в одну группу с Джеком. Следовательно, вероятность 19/59.
11. У нас есть две монеты: A и B. Для каждого броска монеты A вероятность выпадения орла равна 1/2, а для каждого броска монеты B вероятность выпадения орла составляет 1/3. Об этом говорит сайт https://intellect.icu . Все подбрасывания одной монеты независимы. Выбираем монету наугад и подбрасываем до головы. Вероятность выбора монеты A равна ¼, а монеты B - 3/4. Какое ожидается количество бросков, чтобы получить первым орла?
- a) 2,75 *
- b) 3,35
- c) 4,13
- d) 5,33
Решение: (A)
Если выбрана монета A, то количество раз, когда монета будет подброшена для гарантированного орла, равно 2, аналогично для монеты B это 3. Таким образом, количество раз будет
Броски = 2 * (1/4. [вероятность выбора монеты A]) + 3 * (3/4. [вероятность выбора монеты B])
= 2,75
Это просто применение Закона полного математического ожидания закон полного математического ожидания , правило башни , закон адама , теорема сглаживания , .
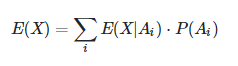
В нашем случае определения такие:
x - случайная величина для количества бросков, которые нужно кинуть орлом вверх,
А1 : Монета с вероятностью выпала , равной 1/2 выбора,
А2 : Монета с вероятностью выпадения, равной 1/3 выбора.
Из геометрического распределения
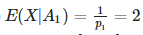 и
и
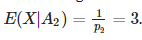 И
И
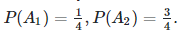 .
.
Следовательно, мы имеем
Думаю, вы уже знакомы с Законом полной вероятности . Он имеет структуру, аналогичную Закону полного ожидания, но для вероятностей:
Можно сказать, что E(X) — средневзвешенное значение условных ожиданий.
12. Предположим, компания по страхованию жизни продает полис страхования жизни на один год на 240000 долларов 25-летней женщине за 210 долларов. Вероятность того, что женщина переживет год, равна 0,999592. Найдите ожидаемую прибыль этого полиса для страховой компании.
- a) 131 доллар
- b) 140 долларов
- c) 112 долларов *
- d) 125 $
Решение: (c)
P (компания теряет деньги) = 0,000408 (Вероятность того, что женщина умрет )
P (компания не теряет деньги) = 0,99592 (Вероятность того, что женщина переживет год . )
Сумма денег, которую компания должна выплатить (теряет), если женщина умрет, составляет 240000 долларов - стоимость полиса в 210 долларов = 239790 долларов.
В то время как деньги, которые он получает, составляют 210 долларов
Ожидаемые деньги, которые компания должна будет отдать = 239790 * 0,000408 = 97,8 долларов
Ожидаемые деньги, которые получит компания = 210 долларов
Ожидаемая прибыль = Доходы - Расходы
Доходы для страховой компании составляют 210 долларов (цена полиса), а расходы составляют ожидаемые выплаты по полисам, что равно 98 долларам.
Таким образом, ожидаемая прибыль страховой компании составляет:
Ожидаемая прибыль = 210 долларов - 98 долларов = 112 долларов.
ожидаемая прибыль страховой компании составляет 112 долларов.
13. 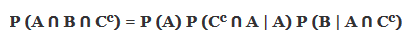
Решение: (A)
Вышеприведенное утверждение верно. Вам нужно знать, что
P (A / B) = P (AꓵB) / P (B)
P (C c A | A) = P (C c AꓵA) / P (A) = P (C c A) / P (A)
P (B | A ꓵ C c ) = P (AꓵBꓵC c ) / P (A ꓵ C c )
Умножив эти три, мы получим - P (AꓵBꓵC c ), следовательно, справедливы уравнения
14. Когда событие А не зависит от самого себя?
- a) Всегда
- b) тогда и только тогда, когда P (A) = 0
- C) Если и только если P (A) = 1
- D) Если и только если P (A) = 0 или 1 *
Решение: (D)
Событие может быть независимым от самого себя только тогда, когда оно не произойдет или когда оно обязательно произойдет. События A и B независимы, если P (AꓵB) = P (A) * P (B). Теперь, если B = A, P (AꓵA) = P (A), когда P (A) = 0 или 1.
15. Предположим, вы находитесь в финальном раунде игрового шоу «Давай заключим сделку» и должны выбрать одну из трех дверей - 1, 2 и 3. За одной из трех дверей стоит машина, а за двумя другими дверями - козы. Допустим, вы выбрали Дверь 1, и хост открывает Дверь 3, за которой стоит коза. Чтобы гарантировать вероятность вашего выигрыша, какой из следующих вариантов вы бы выбрали.
- A) Переключите свой выбор *
- b) Сохраните свой выбор
- c) Неважно, что вероятность выигрыша или проигрыша одинакова с открытием одной двери или без нее.
Решение: (A)
Я бы рекомендовал прочитать эту статью для детального обсуждения проблемы Монти Холла.
16. Перекрестное оплодотворение красного и белого цветов дает красные цветы в 25% случаев. Теперь мы перекрестно оплодотворяем пять пар красных и белых цветков и производим пять потомков. Какова вероятность того, что в пятерке потомков нет красных цветочных растений?
- a) 23,7% *
- b) 37,2%
- c) 22,5%
- d) 27,3%
Решение: (A)
Вероятность того, что потомство будет красным, составляет 0,25, таким образом, вероятность того, что потомство не будет красным, составляет 0,75. Поскольку все пары независимы друг от друга, вероятность того, что все потомки не красные, будет (0,75. 5 = 0,237. Вы можете думать об этом как о биноме со всеми ошибками.
17. В колесе рулетки 38 ячеек - 18 красных, 18 черных и 2 зеленых. Вы играете в пять игр и всегда делаете ставки на красные слоты. Сколько игр вы можете рассчитывать на победу?
- a) 1,1165
- b) 2.3684 *
- c) 2.6316
- d) 4,7368
Решение: (B)
Вероятность того, что в любом спине будет красное, составляет 18/38. Теперь вы играете в игру 5 раз, и все игры независимы друг от друга. Таким образом, количество игр, которые вы можете выиграть, составит 5 * (18/38) = 2,3684.
18. На колесе рулетки 38 ячеек, 18 красных, 18 черных и 2 зеленых. Вы играете в пять игр и всегда делаете ставку на красное. Какова вероятность того, что вы выиграете все 5 игр?
- a) 0,0368
- b) 0,0238 *
- c) 0,0526
- d) 0,0473
Решение: (B)
Вероятность того, что в любом спине будет красное, составляет 18/38. Теперь вы играете в игру 5 раз, и все игры независимы друг от друга. Таким образом, вероятность того, что вы выиграете все игры, составляет (18/38)^ 5 = 0,0238.
19. Некоторые результаты тестов имеют нормальное распределение со средним значением 18 и стандартным отклонением 6. Какая доля участников тестирования набрала от 18 до 24?
- a) 20%
- b) 22%
- c) 34% *
- D) Ничего из вышеперечисленного
Решение: (C)
Итак, здесь нам нужно будет вычислить баллы Z для значений 18 и 24. Мы можем легко сделать это, положив выборочное среднее значение как 18, а среднее значение генеральной совокупности как 18 с σ = 6 и вычислив Z. Точно так же мы можем вычислить Z для выборочного среднего значения как 24.
Z = (X-μ) / σ
Следовательно, для 26 как X,
Z = (18-18) / 6 = 0, глядя на таблицу Z, мы обнаруживаем, что 50% людей имеют оценки ниже 18.
Для 24 как X
Z = (24-18) / 6 = 1, глядя на таблицу Z, мы обнаруживаем, что у 84% людей оценка ниже 24.
Таким образом, около 34% людей имеют оценку от 18 до 24.
20. В банке 4 шарика. 3 красных и 1 белый. После каждого розыгрыша вытягиваются два шарика с заменой. Какова вероятность того, что шарик одного цвета будет нарисован дважды?
- a) 1/2
- b) 1/3
- c) 5/8 *
- d) 1/8
Решение: (C)
Если шарики одного цвета, то это будет 3/4 * 3/4 + 1/4 * 1/4 = 5/8.
21. Какое из следующих событий наиболее вероятно?
- a) По крайней мере, одна 6, когда брошено 6 кубиков *
- b) Как минимум 2 шестерки при выпадении 12 кубиков
- C) Как минимум 3 шестерки при выпадении 18 кубиков
- D) Все вышеперечисленное имеют одинаковую вероятность
Решение: (A)
Вероятность выпадения цифры 6 при броске кубиков равна P (6. = (1/6. & P (6 ') = (5/6). Таким образом, вероятность
Случай 1: (1/6) * (5/6) 5 = 0,06698
Случай 2: (1/6) 2 * (5/6) 10 = 0,00448
Случай 3: (1/6) 3 * (5/6) 15 = 0,0003
Таким образом, наибольшая вероятность - случай 1.
22. Предположим, вас взяли на собеседование на техническую роль. 50% людей, присутствовавших на первом собеседовании, получили приглашение на второе собеседование. 95% людей, которым позвонили на второе собеседование, остались довольны своим первым собеседованием. 75% людей, которым не позвонили во второй раз, тоже остались довольны своим первым интервью. Если вы почувствовали себя хорошо после первого собеседования, какова вероятность того, что вам позвонят на втором собеседовании?
- a) 66%
- b) 56% *
- c) 75%
- d) 85%
Решение: (B)
Предположим, что первый раунд интервью дали 100 человек. 50 человек получили приглашение на собеседование во втором туре. 95% из них положительно оценили свое интервью, что составляет 47,5%. 50 человек не были вызваны на собеседование; из них 75% чувствовали себя примерно хорошо, что составляет 37,5. Таким образом, общее количество людей, которые почувствовали себя хорошо после интервью, составляет (37,5 + 47,5. 85. Таким образом, из 85 человек, которые почувствовали себя хорошо, только 47,5 получили вызов в следующий раунд. Следовательно, вероятность успеха (47,5 / 85. = 0,558.
Другой более распространенный способ решения этой проблемы - это теорема Байя. Я оставляю это на ваше усмотрение.
23. Монета диаметром 1 дюйм бросается на стол, покрытый сеткой линий, расположенных каждые два дюйма друг от друга. Какова вероятность того, что монета приземлится внутри квадрата, не коснувшись ни одной из линий сетки? Вы можете предположить, что бросающий не умеет бросать монету и бросает ее случайным образом. Вы можете предположить, что бросающий не умеет бросать монету и бросает ее случайным образом.
- a) 1/2
- b) 1/4 *
- c) Π / 3
- d) 1/3
Решение: (B)
Подумайте о том, где может быть весь центр монеты, когда она приземляется на сетку в 2 дюйма и не касается линий сетки.
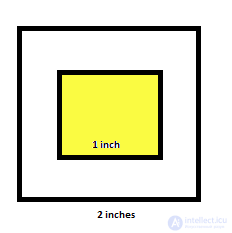
Если желтая область представляет собой квадрат размером 1 дюйм, а внешний квадрат - 2 дюйма. Если центр попадает в желтую область, монета не будет касаться линии сетки. Поскольку общая площадь равна 4, а площадь желтой области равна 1, вероятность равна.

24. Всего 8 луков по 2 зеленого, желтого, оранжевого и красного цветов. Какими способами вы можете выбрать 1 лук?
Решение: (C)
Вы можете выбрать один из четырех разных луков, поэтому вы можете выбрать один лук четырьмя разными способами.
25. Рассмотрим следующую функцию плотности вероятности: Какова вероятность для X≤6, т.е. P (x≤6) 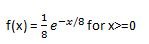 Какова вероятность для X≤6, т.е. P (x≤6)
Какова вероятность для X≤6, т.е. P (x≤6)
- a) 0,3935
- b) 0,5276 *
- c) 0,1341
- d) 0,4724
Решение: (B)
Чтобы вычислить площадь определенной области функции плотности вероятности, нам нужно интегрировать функцию в пределах значений, для которых нам нужно вычислить вероятность.
Следовательно, интегрировав заданную функцию от 0 до 6, получим 0,5276
26. В классе из 30 учеников, какова приблизительно вероятность того, что у двоих из учеников день рождения будет в один и тот же день (определяемый одним и тем же днем и месяцем) (при условии, что это не високосный год)?
Например, ученики, чьи дни рождения 3 января 1993 г. и 3 января 1994 г. будут благоприятным событием.
- a) 49%
- b) 52%
- c) 70% *
- d) 35%
Решение: (C)
Общее количество возможных комбинаций, когда никакие два человека не могут иметь один и тот же день рождения в классе из 30 человек, составляет 30 * (30-1) / 2 = 435.
Итак, в году 365 дней (при условии, что это не високосный год). Таким образом, вероятность того, что у людей будет другой день рождения, будет 364/365. Теперь возможно 870 комбинаций. Таким образом, вероятность того, что у двух людей один и тот же день рождения, равна (364/365) ^ 435 = 0,303.
Таким образом, вероятность того, что у двух людей дни рождения будут в один и тот же день, будет 1 - 0,303 = 0,696.
27. Ахмед играет в лотерею, где он должен выбрать 2 числа от 0 до 9, за которыми следует английский алфавит (из 26 букв). Оба раза он может выбрать одно и то же число. Если его билет совпадает с 2 числами и 1 буквой, выписанными по порядку, он выигрывает главный приз и получает 10405 долларов. Если совпадает только его буква, но одно или оба числа не совпадают, он выигрывает 100 долларов. При любых других обстоятельствах он ничего не выигрывает. Игра стоит ему 5 долларов. Предположим, он выбрал для игры 04R. Какова ожидаемая чистая прибыль от розыгрыша этого билета?
- a) -2,81 $
- b) 2,81 доллара США *
- c) -1,82 доллара США
- D) 1,82 $
Решение: (B)
Ожидаемая стоимость в этом случае
E (X) = P (главный приз) * (10405-5. + P (малый) (100-5. + P (проигрыш) * (- 5.
P (главный приз) = (1/10) * (1/10) * (1/26.
P (small) = 1 / 26–1 / 2600, причина, по которой нам нужно это сделать, состоит в том, что нам нужно исключить случай, когда он получает правильную букву, а также правильные числа. Следовательно, нам нужно удалить сценарий получения письма правильно.
P (проигрыш) = 1-1 / 26-1 / 2600
Следовательно, мы можем уместить значения, чтобы получить ожидаемое значение 2,81 доллара.
28. Предположим, вы продаете бутерброды. 70% выбирают яйцо , остальные - курицу. Какова вероятность продажи двух яичных бутербродов следующим трем покупателям?
- a) 0,343
- b) 0,063
- c) 0,44 *
- d) 0,027
Решение: (C)
Вероятность продажи сэндвича с яйцом составляет 0,7, а сэндвича с курицей - 0,3. Теперь вероятность того, что следующие 3 покупателя закажут 2 сэндвича с яйцом, равна 3 * 0,7 * 0,7 * 0,3 = 0,44. Их можно расположить в любой последовательности, вероятности все равно останутся прежними .
Контекст вопроса: 29 - 30
ВИЧ по-прежнему очень страшная болезнь, на которую стоит даже пройти тестирование. Военные США проверяют своих новобранцев на ВИЧ при вербовке. Их тестируют в трех раундах Elisa (теста на ВИЧ), прежде чем они будут признаны положительными.
Априорная вероятность того, что кто-либо заразится ВИЧ, составляет 0,00148. Истинно положительный показатель для Elisa составляет 93%, а истинно отрицательный показатель - 99%.
29. Какова вероятность того, что новобранец инфицирован ВИЧ, если у него положительный результат первого теста Элизы? Априорная вероятность того, что кто-либо заразится ВИЧ, составляет 0,00148. Истинно положительный показатель для Elisa составляет 93%, а истинно отрицательный показатель - 99%.
- a) 12% *
- b) 80%
- c) 42%
- d) 14%
Решение: (A)
Я рекомендую просмотреть раздел этой статьи, посвященный байесовскому обновлению, для понимания поставленного выше вопроса.
30. Какова вероятность заражения ВИЧ, если у него второй раз положительный результат теста на Элизу.
Априорная вероятность того, что кто-либо заразится ВИЧ, составляет 0,00148. Истинно положительный показатель для Elisa составляет 93%, а истинно отрицательный показатель - 99%.
- a) 20%
- b) 42%
- c) 93% *
- d) 88%
Решение: (C)
Я рекомендую просмотреть раздел этой статьи, посвященный байесовскому обновлению, для понимания поставленного выше вопроса.
31. Предположим, вы играете в игру, в которой мы несколько раз подбрасываем честную монету. Вы уже трижды проиграли, где угадывались орлом, но выпали решки. Какое из следующих утверждений будет правильным в этом случае?
- A) Вам следует угадать орел снова, так как решка уже выпала трижды, и вероятность выпадения орла более высока.
- b) Вам следует говорить решку, потому что угадывание орла не приводит к победе
- C) У вас одинаковая вероятность выигрыша при угадывании любого, поэтому независимо от того, что вы угадываете, вероятность выигрыша или проигрыша составляет 50-50. *
- D) Ни один из этих
Решение: (C)
Это классическая проблема заблуждения игрока / заблуждения Монте-Карло, когда человек ложно начинает думать, что результаты должны сравняться через несколько ходов. Игрок начинает верить, что если мы получили 3 решки, вы должны получить 3 решки. Однако это не так. Результаты сравнялись бы только в бесконечном количестве испытаний.
32. Вывод с использованием частотного подхода всегда будет давать тот же результат, что и байесовский подход.
Решение: (B)
Частотный подход во многом зависит от того, как мы определяем гипотезу, в то время как байесовский подход помогает нам обновить наши предыдущие убеждения. Следовательно, частотный подход может привести к противоположному выводу, если мы сформулируем гипотезу иначе. Следовательно, эти два подхода могут не дать одинаковых результатов.
33. Больничные записи показывают, что 75% пациентов, страдающих каким-либо заболеванием, умирают от него. Какова вероятность выздоровления 4 из 6 случайно выбранных пациентов?
- a) 0,17798
- b) 0,13184
- c) 0,03295 *
- d) 0,35596
Решение: (C)
Думайте об этом как о биномиальном, поскольку есть только 2 исхода: либо пациент умирает, либо он выживает.
Здесь n = 6, а x = 4. p = 0,25 (вероятность жизни (успех)) q = 0,75 (вероятность смерти (неудача))
P (X) = n C x p x q n-x = 6 C 4 (0,25. 4 (0,75. 2 = 0,03295
34. Учащимся одного класса давали два теста для оценки. Двадцать пять процентов класса сдали оба теста, а сорок пять процентов учеников смогли пройти первый тест.
Подсчитайте процент учащихся, сдавших второй тест, при условии, что они смогли сдать и первый тест.
- a) 25%
- b) 42%
- c) 55% *
- d) 45%
Решение: (C)
Это простая проблема условной вероятности. Пусть A будет событием прохождения первого теста.
B - это событие прохождения второго теста.
P (AꓵB) проходит в обоих событиях
P (сдав второй, если он сдал первый) = P (AꓵB) / P (A)
= 0,25 / 0,45, что составляет около 55%
35. Хотя говорят, что вероятность иметь мальчика или девочку одинакова, давайте предположим, что фактическая вероятность иметь мальчика немного выше и составляет 0,51. Предположим, пара планирует завести троих детей. Какова вероятность, что ровно двое из них будут мальчиками?
- a) 0,38 *
- b) 0,48
- c) 0,58
- d) 0,68
- E) 0,78
Решение: (A)
Думайте об этом как о биномиальном распределении, где успех - это мальчик, а неудача - девочка. Поэтому нам нужно рассчитать вероятность получения 2 из трех успехов.
P (X) = n C x p x q n-x = 3 C 2 (0,51) 2 (0,49) 1 = 0,382
36. Рост 10-летних, независимо от пола, точно соответствует нормальному распределению со средним значением 55 дюймов и стандартным отклонением 6 дюймов. Какие из следующих утверждений верно?
- A) Мы ожидаем, что 10-летние дети ростом ниже 55 дюймов будут больше, чем те, кто выше 55 дюймов.
- b) Примерно 95% 10-летних детей имеют рост от 37 до 73 дюймов.
- C) 10-летний ребенок ростом 65 дюймов будет считаться более необычным, чем 10-летний ребенок ростом 45 дюймов.
- D) Ни один из этих *
Решение: (D)
Ни одно из приведенных выше утверждений не соответствует действительности.
37. Около 30% человеческих близнецов однояйцевые, остальные - разнояйцевые. Однояйцевые близнецы обязательно одного пола, половина - самцы, а другая половина - самки. Четверть разнояйцевых близнецов - оба мужчины, четверть - женщины, а половина - смешанные: один мужчина, одна женщина. Вы только что стали отцом близнецов, и вам сказали, что они обе девочки. Учитывая эту информацию, какова вероятность того, что они идентичны?
- a) 50%
- b) 72%
- c) 46% *
- d) 33%
Решение: (C)
Это классическая проблема теоремы Байеса.
P (I) обозначает вероятность быть идентичными, а P (~ I) обозначает вероятность не быть идентичными.
P (идентичный) = 0,3
P (не идентично) = 0,7
P (FF | I) = 0,5
P (ММ | I) = 0,5
P (ММ | ~ I) = 0,25
P (FF | ~ I) = 0,25
P (FM | ~ I) = 0,25
P (I | FF) = 0,46
38. У Василия высокая температура, и врач подозревает, что это брюшной тиф. Конечно, врач хочет провести тест. Результаты теста положительны, когда у пациента действительно тиф в 80% случаев. Тест дает положительный результат, если у пациента нет брюшного тифа в 10% случаев. Если 1% населения болен брюшным тифом, какова вероятность того, что у Василия брюшной тиф при условии положительного результата теста?
- a) 12%
- b) 7% *
- c) 25%
- d) 31,5%
Решение: (B)
Решение:
Нам нужно определить вероятность заболевания брюшным тифом при положительном результате теста.
Используя теорему Байеса:
P(тиф|положительный результат) = P(положительный результат|тиф)*P(брюшной тиф)/P(положительный результат)
P(положительный результат|брюшной тиф) = 0,8
P (брюшной тиф) = 0,01
P(положительный результат) = P(положительный результат|брюшной тиф) P(брюшной тиф) + P(положительный результат|не брюшной тиф) P(не брюшной тиф) = 0,8*0,01+0,1*0,99
P (тиф | положительный результат) = 0,0747.
39. У Володи в руке две монеты. Из двух монет одна настоящая, а вторая - неисправная с хвостами на обеих сторонах. Он завязывает себе глаза, выбирает случайную монету и подбрасывает ее в воздух. Монета падает решкой вверх. Какова вероятность того, что этот хвост покажет неисправная монета?
- a) 1/3
- b) 2/3 *
- c) 1/2
- d) 1/4
Решение: (B)
Нам нужно найти вероятность того, что монета неисправна, учитывая, что на ней были решки.
P (неисправен) = 0,5
P (получение решки) = 3/4
P (дефект и хвосты) = 0,5 * 1 = 0,5
Следовательно, вероятность того, что монета окажется неисправной, учитывая, что на ней выпадет решка, будет 2/3.
40. Муха живет 4-6 дней. Какова вероятность того, что муха погибнет ровно через 5 дней?
- a) 1/2
- b) 1/4
- c) 1/3
- d) 0 *
Решение: (D)
Здесь, поскольку вероятности непрерывны, вероятности образуют массовую функцию. Вероятность определенного события рассчитывается путем нахождения площади под кривой для данных условий. Так как мы пытаемся вычислить вероятность смерти мухи ровно через 5 дней - площадь под кривой будет равна 0. Кроме того, если подумать, вероятность того, что муха умрет ровно через 5 дней, для нас невозможно даже выяснить, поскольку мы не можем измерить с бесконечной точностью, если бы это было ровно 5 дней.
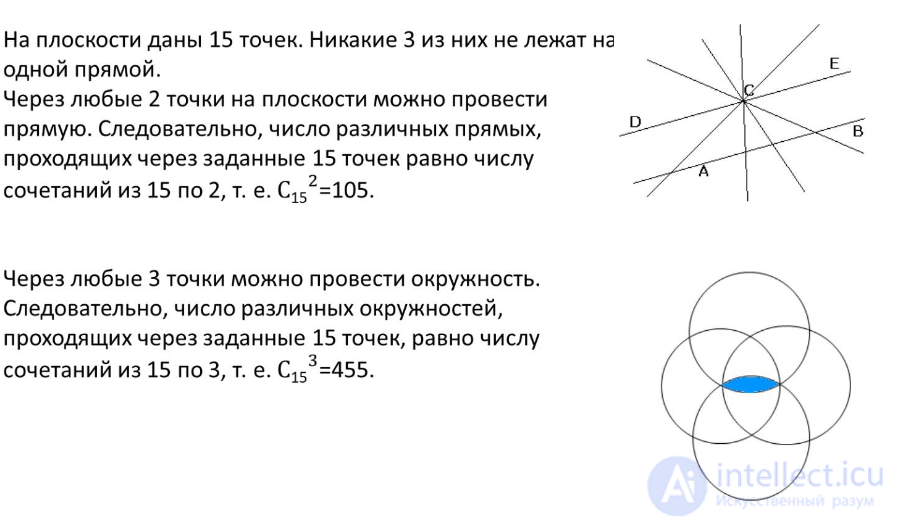
41. Задача о точках на плоскости. a) На плоскости даны 15 точек. Никакие 3 из них не лежат на одной прямой. Сколько различных прямых можно провести? б) Сколько окружностей определяют эти точки?
- а 105 * и б 455
- а 10 и б 20
- а 5 и б 3
- а 1005 и б 103
Решение задачи о точках на плоскости
42. Задача о ладьях. Сколькими способами можно поставить на шахматном поле белую и черную ладьи так, чтобы они не били друг друга.
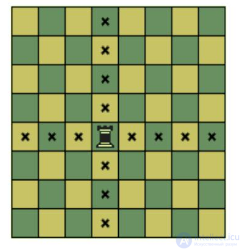
Решение
Белую ладью можно поставить на любую из 64 клеток. Она побьет 15 клеток: 7 по вертикали, 7 по горизонтали и ту,на которой она стоит, независимо, где бы она не стояла. Остается 64 - 15=49 мест, чтобы поставить черную ладью. Значит, число способов поставить обе ладьи так, чтобы они не били друг друга равно 64*49=3136.Ответ: 3136 способов.
43. Задача о встрече .Два студента договорились встретиться в некотором месте между 9 и 10 часами. Причем, каждый ждет другого в Какова вероятность, что они встретятся?
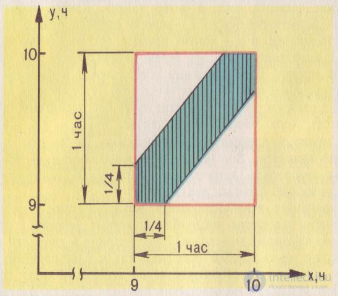
решение

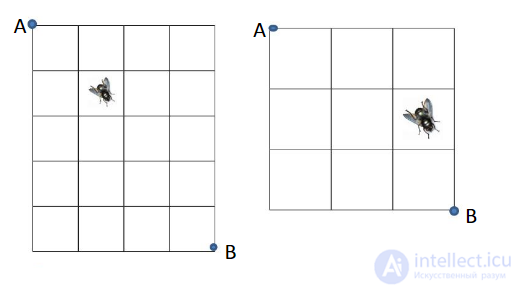
44. Задача о мухе. Муха ползет по решетке размером 3х3 из точки А в точку В, двигаясь все время вправо или вниз. Сколько различных маршрутов может выбрать муха? Как изменится ответ в задаче для решетки 4х5?
- 15 и 20
- 5 и 16
- 20 и 126 *
- 100 и 200

45. Задача озвездочете. Некий властелин разгневался на звездочета и повелел палачу отрубить ему голову. Однако в последний момент властелин смягчился и решил дать звездочету возможность спастись. Он взял 2 черных и 2 белых шара и предложил звездочету произвольным образом распределить их по 2 урнам. Палач должен выбрать наугад одну из урн и наугад вытащить из нее шар. Если шар окажется белым, то звездочет будет помилован, а если черным, казнен. Как
должен звездочет распределить шары по 2 урнам, чтобы иметь наибольшее число шансов спастись?
- ответ а
- ответ б
- ответ в *
- ответ г

Решение
Пусть звездочет положит в каждую урну по 1 белому и по 1 черному шару (рис. a). В этом случае безразлично, к какой урне подойдет палач.
Из любой урны он с вероятностью Р= ½ вынет белый шар. Значит, и вероятность спастись звездочету равна ½.
Вероятность спастись будет также равна ½, если звездочет положит в одну урну 2 белых шара, а в другую 2 черных (рис. б).
Палач с равной вероятностью может подойти как к «белой», так и к «черной» урне.
Пусть звездочет положит в одну урну белый шар, а в другую 1 белый и 2 черных (рис. в). Если палач подойдет к 1-ой урне, то звездочет спасется наверняка (Р=1). Если палач подойдет ко 2-ой урне, то вероятность спастись у звездочета Р=⅓.
Так как Р выбора урны равна ½ , то полная вероятность спастись равна Р=(½*1)+(½*⅓)=⅔.
Если звездочет положит в одну урну черный шар, а в другую-1 черный и 2 белых (рис. г), то вероятность спастись –наименьшая:
Р=(½*0)+(½*⅔)= ⅓.
Таким образом, наибольшие шансы спастись соответствуют (рис. в).
46. Задача «Блуждание в лабиринте» На рисунке изображен лабиринт, в котором хранятся сокровища и имеется западня (кобра). Неудачливые охотники за сокровищами, попадая в западню, погибают. Какова вероятность избежать западни и добраться до сокровищ?
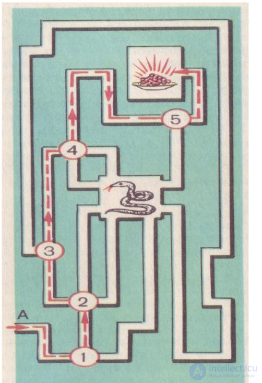
Решение задачи
Пройдя от А до пункта 1, искатель может пойти прямо или повернуть налево. Ясно, что вероятность выбора Р= ½.
Попав в пункт 2, искатель выбирает путь-прямо, или направо, или налево.
Вероятность выбора Р=⅓.Тогда вероятность попасть из А в пункт 3равна Р= ½ * ⅓, т.е. повернуть в пункте 1 налево с Р= ½ и в пункте 2 налево с Р=⅓.
Чтобы из А добраться из пункта 4, необходимо из пункта 3 с Р= ½ пройти прямо, т.е. Р= ½ * ⅓* ½.
Ясно, что Р добраться из А в пункт 5 равна Р= ½ * ⅓* ½* ⅓.
Вероятность попасть из А в хранилище Р= ½ * ⅓* ½* ⅓* ½=1/72.
Вероятность попасть в западню и погибнуть равна Р=71/72.
47. Задача об отличном билете Назовем билет с номером от 000000 до 999999 отличным , если разность двух соседних цифр равна 5. Найти число отличных
билетов.
- 106
- 10 * 95
- 106 - 10 * 95 *
- 1- 10 * 95

решение

48. Задача «О кассире». Чтобы быстрее подсчитать мелочь в конце рабочего дня, кассир заранее складывает рублевые монеты столбиками по 10 монет в каждом. При этом каждая монета в столбике с равной вероятностью лежит решкой или орлом вверх. Сколько всего есть способов положить 10 монет в столбик так, чтобы ровно 4 из них лежали орлом вверх?
решение

49.Задача «Игра в шахматы» . Остап Бендер играет 8 шахматных партий против членов шахматного клуба. Остап играет плохо, поэтому вероятность выигрыша им каждой партии равна 0, 01. Найти вероятность того, что Остап выиграет хотя бы 1 партию.
Решение

50. Задача о шарах в урне. В урну, содержащую два шара , опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равно возможны различные предположения о первоначальном цвете шаров.
Решение
Обытие А-извлечен белый шар. Возможны гипотезы о первоначальном составе шаров: В1 – белых шаров нет, В2 – один белый шар, В3- два белых шара. Так как они равно возможны, то вероятность каждой гипотезы равна 1/3.Условная вероятность извлечения белого шара, если верна первая гипотеза, то есть в урне не было белых шаров, равна Р(А/В1)=1/3, условная вероятность извлечения белого шара при наличии в урне двух белых шаров равна Р(А/В2)=1, и вероятность извлечь белый шар, если в урне был один белый шар, равна Р(А/В3)=2/3.Вероятность извлечь белый шар вычисляем по формуле полной вероятности: Р(a)=1/3*1/3+1/3*2/3+1/3*1=2/3.
51. задача о шарах. В одной из урн 10 белых и 6 черных шаров , в другой – 7 белых и 9 черных шаров. Произвольно выбирают урну и из нее вынимают шар. Он белый. Чему равна вероятность того, что и второй шарик, наугад вынутый из этой урны, окажется белым?
Решение
Событие А – в каждом из двух испытаний вынут белый шар.
В1 – гипотеза выбрать первую урну, В2 – выбрать вторую урну, Р(В1)=Р(В2)=1/2.
Условные вероятности: Р(А/В1)=10/16*9/15=15/40-вероятность вынуть белый шар
из первой урны в первом и втором испытании.
Р(А/В2)=7/16*6/15=7/40- вероятность подряд вынуть белый шар из второй урны.
Р(a)=1/2*15/40+1/2*7/40=1/2*22/40=11/40
52. задача о шарах в урне. В первой урне 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар. (Р=0,5)
РешениеВведем гипотезы о цвете извлеченных шаров из каждой урны: В1 - из каждой урны извлечен белый шар. Р(В1)=8/10*4/20=4/25.В2 – из каждой урны извлечен черный шар. Р(В2)=2/10*16/20=4/25.В3 – из урн извлечен 1белый и 1 черный шар. Р(В3)=8/10*16/20 + 2/10*4/20 = 17/25Событие А – шар белый. Рассмотрим условные вероятности: из двух шаров вынуть белый при этих гипотезах Р(А/В1)=1, Р(А/В2)=0, Р(А/В3)=1/2, тогда по формуле полной вероятности Р(a)=1*4/25+ 0*4/25 + 1/2*17/25=4/25+17/50 = ½.
Если у вас есть вопросы или сомнения, не стесняйтесь размещать их ниже.
См. также
- Событие
- Вероятность
- Случайная величина
- Случайное событие
- Дискретная случайная величина
- непрерывная случайная величина
- Плотность вероятности
- Парадокс Монти Холла
- Линейная частичная информация
- Математическая статистика
- Вероятностное пространство
- Интерпретации вероятности
- Теорема Баеса
- Предусмотрительное моделирование
- Другие тесты
Исследование, описанное в статье про собеседование по теории вероятностей, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое собеседование по теории вероятностей, тесты по теории вероятности
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория вероятностей. Математическая статистика и Стохастический анализ
Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.
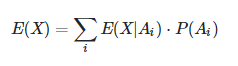
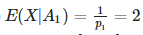 и
и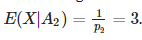 И
И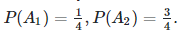 .
.

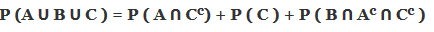
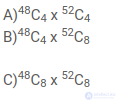
 , то второй бросок должен быть каким угодно, только не
, то второй бросок должен быть каким угодно, только не  , что означает, что для броска 2 существует 5 «успешных» исходов (из 6 возможных). Итак, поскольку каждый бросок не зависит от предыдущих бросков, мы перемножаем их вероятности «успеха». Вероятность того, что после двух бросков не выпадет ни одного повтора, равна 6/6×5/6=5/6, тоесть с вероятностью 83,3%.
, что означает, что для броска 2 существует 5 «успешных» исходов (из 6 возможных). Итак, поскольку каждый бросок не зависит от предыдущих бросков, мы перемножаем их вероятности «успеха». Вероятность того, что после двух бросков не выпадет ни одного повтора, равна 6/6×5/6=5/6, тоесть с вероятностью 83,3%.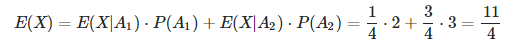

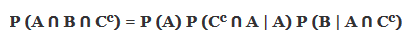


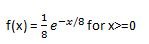 Какова вероятность для X≤6, т.е. P (x≤6)
Какова вероятность для X≤6, т.е. P (x≤6)













Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ