Лекция
Привет, Вы узнаете о том , что такое доверительный интервал, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое доверительный интервал, доверительная вероятность , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
В предыдущих 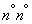 мы рассмотрели вопрос об оценке неизвестного параметра
мы рассмотрели вопрос об оценке неизвестного параметра 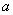 одним числом. Такая оценка называется «точечной». В ряде задач требуется не только найти для параметра
одним числом. Такая оценка называется «точечной». В ряде задач требуется не только найти для параметра 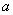 подходящее численное значение, но и оценить его точность и надежность. Требуется знать - к каким ошибкам может привести замена параметра
подходящее численное значение, но и оценить его точность и надежность. Требуется знать - к каким ошибкам может привести замена параметра 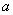 его точечной оценкой
его точечной оценкой 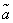 и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы?
и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы?
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка 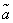 в значительной мере случайна и приближенная замена
в значительной мере случайна и приближенная замена 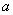 на
на 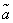 может привести к серьезным ошибкам.
может привести к серьезным ошибкам.
Чтобы дать представление о точности и надежности оценки 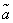 , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
, в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
Пусть для параметра 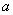 получена из опыта несмещенная оценка
получена из опыта несмещенная оценка 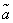 . Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность
. Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность 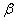 (например,
(например, 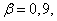
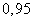 или
или 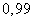 ) такую, что событие с вероятностью
) такую, что событие с вероятностью 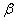 можно считать практически достоверным, и найдем такое значение
можно считать практически достоверным, и найдем такое значение 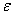 , для которого
, для которого
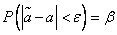 . (14.3.1)
. (14.3.1)
Тогда диапазон практически возможных значений ошибки, возникающей при замене 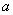 на
на 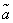 , будет
, будет 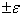 ; большие по абсолютной величине ошибки будут появляться только с малой вероятностью
; большие по абсолютной величине ошибки будут появляться только с малой вероятностью 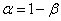 .
.
Перепишем (14.3.1) в виде:
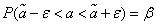 . (14.3.2)
. (14.3.2)
Равенство (14.3.2) означает, что с вероятностью 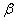 неизвестное значение параметра
неизвестное значение параметра 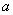 попадает в интервал
попадает в интервал
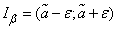 . (14.3.3)
. (14.3.3)
При этом необходимо отметить одно обстоятельство. Ранее мы неоднократно рассматривали вероятность попадания случайной величины в заданный неслучайный интервал. Здесь дело обстоит иначе: величина 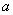 не случайна, зато случаен интервал
не случайна, зато случаен интервал  . Случайно его положение на оси абсцисс, определяемое его центром
. Случайно его положение на оси абсцисс, определяемое его центром 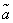 ; случайна вообще и длина интервала
; случайна вообще и длина интервала 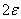 , так как величина
, так как величина 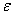 вычисляется, как правило, по опытным данным. Поэтому в данном случае лучше будет толковать величину
вычисляется, как правило, по опытным данным. Поэтому в данном случае лучше будет толковать величину 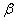 не как вероятность «попадания» точки
не как вероятность «попадания» точки 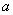 в интервал
в интервал  , а как вероятность того, что случайный интервал
, а как вероятность того, что случайный интервал  накроет точку
накроет точку 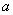 (рис. 14.3.1).
(рис. 14.3.1).
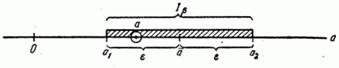
Рис. 14.3.1.
Вероятность 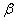 принято называть доверительной вероятностью, а интервал
принято называть доверительной вероятностью, а интервал  - доверительным интервалом. Границы интервала
- доверительным интервалом. Границы интервала  :
: 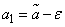 и
и  называются доверительными границами.
называются доверительными границами.
Дадим еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра 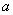 , совместимых с опытными данными и не противоречащих им. Действительно, если условиться считать событие с вероятностью
, совместимых с опытными данными и не противоречащих им. Действительно, если условиться считать событие с вероятностью 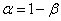 практически невозможным, то те значения параметра
практически невозможным, то те значения параметра 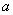 , для которых
, для которых 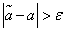 , нужно признать противоречащими опытным данным, а те, для которых
, нужно признать противоречащими опытным данным, а те, для которых 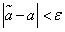 , - совместимыми с ними.
, - совместимыми с ними.
Перейдем к вопросу о нахождении доверительных границ  и
и 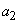 .
.
Пусть для параметра 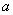 имеется несмещенная оценка
имеется несмещенная оценка 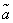 . Если бы нам был известен закон распределения величины
. Если бы нам был известен закон распределения величины 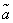 , задача нахождения доверительного интервала была бы весьма проста: достаточно было бы найти такое значение
, задача нахождения доверительного интервала была бы весьма проста: достаточно было бы найти такое значение 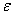 , для которого
, для которого
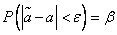 .
.
Затруднение состоит в том, что закон распределения оценки 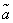 зависит от закона распределения величины
зависит от закона распределения величины 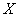 и, следовательно, от его неизвестных параметров (в частности, и от самого параметра
и, следовательно, от его неизвестных параметров (в частности, и от самого параметра 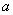 ).
).
Чтобы обойти это затруднение, можно применить следующий грубо приближенный прием: заменить в выражении для 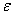 неизвестные параметры их точечными оценками. При сравнительно большом числе опытов
неизвестные параметры их точечными оценками. При сравнительно большом числе опытов  (порядка
(порядка  ) этот прием обычно дает удовлетворительные по точности результаты.
) этот прием обычно дает удовлетворительные по точности результаты.
В качестве примера рассмотрим задачу о доверительном интервале для математического ожидания.
Пусть произведено  независимых опытов над случайной величиной
независимых опытов над случайной величиной 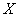 , характеристики которой - математическое ожидание
, характеристики которой - математическое ожидание 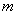 и дисперсия
и дисперсия 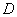 - неизвестны. Для этих параметров получены оценки:
- неизвестны. Для этих параметров получены оценки:
 ;
;  . (14.3.4)
. (14.3.4)
Требуется построить
доверительный интервал 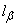 , соответствующий доверительной вероятности
, соответствующий доверительной вероятности 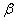 , для математического ожидания
, для математического ожидания 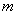 величины
величины 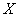 .
.
При решении этой задачи воспользуемся тем, что величина 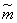 представляет собой сумму
представляет собой сумму  независимых одинаково распределенных случайных величин
независимых одинаково распределенных случайных величин 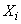 , и, согласно центральной предельной теореме, при достаточно большом
, и, согласно центральной предельной теореме, при достаточно большом  ее закон распределения близок к нормальному. Об этом говорит сайт https://intellect.icu . На практике даже при относительно небольшом числе слагаемых (порядка
ее закон распределения близок к нормальному. Об этом говорит сайт https://intellect.icu . На практике даже при относительно небольшом числе слагаемых (порядка 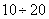 ) закон распределения суммы можно приближенно считать нормальным. Будем исходить из того, что величина
) закон распределения суммы можно приближенно считать нормальным. Будем исходить из того, что величина 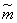 распределена по нормальному закону. Характеристики этого закона - математическое ожидание и дисперсия - равны соответственно
распределена по нормальному закону. Характеристики этого закона - математическое ожидание и дисперсия - равны соответственно 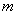 и
и 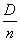 (см. гл. 13
(см. гл. 13 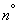 13.3). Предположим, что величина
13.3). Предположим, что величина 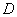 нам известна, и найдем такую величину
нам известна, и найдем такую величину 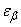 для которой
для которой
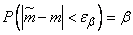 . (14.3.5)
. (14.3.5)
Применяя формулу (6.3.5) главы 6, выразим вероятность в левой части (14.3.5) через нормальную функцию распределения
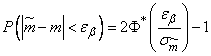 . (14.3.6)
. (14.3.6)
где 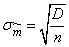 - среднее квадратическое отклонение оценки
- среднее квадратическое отклонение оценки 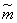 .
.
Из уравнения

находим значение 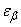 :
:
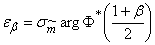 , (14.3.7)
, (14.3.7)
где 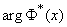 - функция, обратная
- функция, обратная 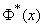 , т. е. такое значение аргумента, при котором нормальная функция распределения равна
, т. е. такое значение аргумента, при котором нормальная функция распределения равна 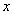 .
.
Дисперсия 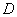 , через которую выражена величина
, через которую выражена величина 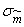 , нам в точности не известна; в качестве ее ориентировочного значения можно воспользоваться оценкой
, нам в точности не известна; в качестве ее ориентировочного значения можно воспользоваться оценкой 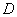 (14.3.4) и положить приближенно:
(14.3.4) и положить приближенно:
 . (14.3.8)
. (14.3.8)
Таким образом, приближенно решена задача построения доверительного интервала, который равен:
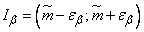 , (14.3.9)
, (14.3.9)
где 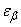 определяется формулой (14.3.7).
определяется формулой (14.3.7).
Чтобы избежать при вычислении 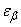 обратного интерполирования в таблицах функции
обратного интерполирования в таблицах функции 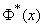 , удобно составить специальную таблицу (см. табл. 14.3.1), где приводятся значения величины
, удобно составить специальную таблицу (см. табл. 14.3.1), где приводятся значения величины
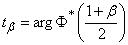
в зависимости от 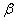 . Величина
. Величина 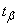 определяет для нормального закона число средних квадратических отклонений, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в полученный участок была равна
определяет для нормального закона число средних квадратических отклонений, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в полученный участок была равна 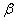 .
.
Через величину 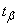 доверительный интервал выражается в виде:
доверительный интервал выражается в виде:
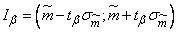 .
.
Таблица 14.3.1
|
|
|
|
|
|
|
|
|
|
0,80 |
1,282 |
0,86 |
1,475 |
0,91 |
1,694 |
0,97 |
2,169 |
|
0,81 |
1,310 |
0,87 |
1,513 |
0,92 |
1,750 |
0,98 |
2,325 |
|
0,82 |
1,340 |
0,88 |
1,554 |
0,93 |
1,810 |
0,99 |
2,576 |
|
0,83 |
1,371 |
0,89 |
1,597 |
0,94 |
1,880 |
0,9973 |
3,000 |
|
0,84 |
1,404 |
0,90 |
1,643 |
0,95 |
1,960 |
0,999 |
3,290 |
|
0,85 |
1,439 |
|
|
0,96 |
2,053 |
|
|
Пример 1. Произведено 20 опытов над величиной 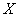 ; результаты приведены в таблице 14.3.2.
; результаты приведены в таблице 14.3.2.
Таблица 14.3.2
|
|
|
|
|
|
|
|
|
|
1 |
10,5 |
6 |
10,6 |
11 |
10,6 |
16 |
10,9 |
|
2 |
10,8 |
7 |
10,9 |
12 |
11,3 |
17 |
10,8 |
|
3 |
11,2 |
8 |
11,0 |
13 |
10,5 |
18 |
10,7 |
|
4 |
10,9 |
9 |
10,3 |
14 |
10,7 |
19 |
10,9 |
|
5 |
10,4 |
10 |
10,8 |
15 |
10,8 |
20 |
11,0 |
Требуется найти оценку 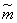 для математического ожидания
для математического ожидания 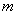 величины
величины 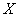 и построить доверительный интервал, соответствующий доверительной вероятности
и построить доверительный интервал, соответствующий доверительной вероятности  .
.
Решение. Имеем:
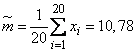 .
.
Выбрав за начало отсчета 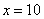 , по третьей формуле (14.2.14) находим несмещенную оценку
, по третьей формуле (14.2.14) находим несмещенную оценку  :
:
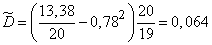 ;
;
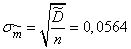 .
.
По таблице 14.3.1 находим 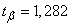 ;
;
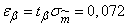 .
.
Доверительные границы:
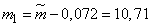 ;
;
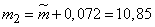 .
.
Доверительный интервал:
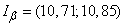 .
.
Значения параметра 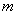 , лежащие в этом интервале, являются совместными с опытными данными, приведенными в таблице 14.3.2.
, лежащие в этом интервале, являются совместными с опытными данными, приведенными в таблице 14.3.2.
Аналогичным способом может быть построен доверительный интервал и для дисперсии.
Пусть произведено  независимых опытов над случайной величиной
независимых опытов над случайной величиной 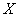 с неизвестными параметрами
с неизвестными параметрами 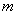 и
и 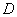 , и для дисперсии
, и для дисперсии 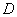 получена несмещенная оценка:
получена несмещенная оценка:
 , (14.3.11)
, (14.3.11)
где
 .
.
Требуется приближенно построить доверительней интервал для дисперсии.
Из формулы (14.3.11) видно, что величина 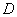 представляет собой сумму
представляет собой сумму  случайных величин вида
случайных величин вида 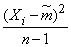 . Эти величины не являются независимыми, так как в любую из них входит величина
. Эти величины не являются независимыми, так как в любую из них входит величина 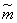 , зависящая от всех остальных. Однако можно показать, что при увеличении
, зависящая от всех остальных. Однако можно показать, что при увеличении  закон распределения их суммы тоже приближается к нормальному. Практически при
закон распределения их суммы тоже приближается к нормальному. Практически при 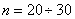 он уже может считаться нормальным.
он уже может считаться нормальным.
Предположим, что это так, и найдем характеристики этого закона: математическое ожидание и дисперсию. Так как оценка 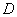 - несмещенная, то
- несмещенная, то
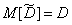 .
.
Вычисление дисперсии 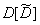 связано со сравнительно сложными выкладками, поэтому приведем ее выражение без вывода:
связано со сравнительно сложными выкладками, поэтому приведем ее выражение без вывода:
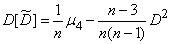 , (14.3.12)
, (14.3.12)
где 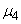 - четвертый центральный момент величины
- четвертый центральный момент величины 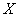 .
.
Чтобы воспользоваться этим выражением, нужно подставить в него значения 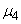 и
и 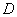 (хотя бы приближенные). Вместо
(хотя бы приближенные). Вместо 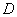 можно воспользоваться его оценкой
можно воспользоваться его оценкой  . В принципе четвертый центральный момент
. В принципе четвертый центральный момент 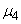 тоже можно заменить его оценкой, например величиной вида:
тоже можно заменить его оценкой, например величиной вида:
 , (14.3.13)
, (14.3.13)
но такая замена даст крайне невысокую точность, так как вообще при ограниченном числе опытов моменты высокого порядка определятся с большими ошибками. Однако на практике часто бывает, что вид закона распределения величины 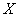 известен заранее: неизвестны лишь его параметры. Тогда можно попытаться выразить
известен заранее: неизвестны лишь его параметры. Тогда можно попытаться выразить 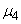 через
через 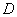 .
.
Возьмем наиболее часто встречающийся случай, когда величина 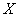 распределена по нормальному закону. Тогда ее четвертый центральный момент выражается через дисперсию (см. гл. 6
распределена по нормальному закону. Тогда ее четвертый центральный момент выражается через дисперсию (см. гл. 6 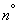 6.2):
6.2):
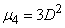 ,
,
и формула (14.3.12) дает
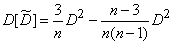
или
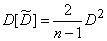 . (14.3.14)
. (14.3.14)
Заменяя в (14.3.14) неизвестное 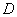 его оценкой
его оценкой  , получим:
, получим:
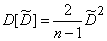 , (14.3.15)
, (14.3.15)
откуда
 . (14.3.16)
. (14.3.16)
Момент 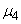 можно выразить через
можно выразить через 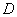 также и в некоторых других случаях, когда распределение величины
также и в некоторых других случаях, когда распределение величины 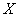 не является нормальным, но вид его известен. Например, для закона равномерной плотности (см. главу 5) имеем:
не является нормальным, но вид его известен. Например, для закона равномерной плотности (см. главу 5) имеем:
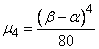 ;
;  ,
,
где 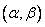 - интервал, на котором задан закон. Следовательно,
- интервал, на котором задан закон. Следовательно,
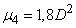 .
.
По формуле (14.3.12) получим:
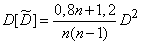 ,
,
откуда находим приближенно
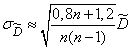 . (14.3.17)
. (14.3.17)
В случаях, когда вид закона распределения величины 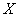 неизвестен, при ориентировочной оценке величины
неизвестен, при ориентировочной оценке величины 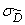 рекомендуется все же пользоваться формулой (14.3.16), если нет специальных оснований считать, что этот закон сильно отличается от нормального (обладает заметным положительным или отрицательным эксцессом).
рекомендуется все же пользоваться формулой (14.3.16), если нет специальных оснований считать, что этот закон сильно отличается от нормального (обладает заметным положительным или отрицательным эксцессом).
Если ориентировочное значение 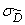 тем или иным способом получено, то можно построить доверительный интервал для дисперсии, аналогично тому, как мы строили его для математического ожидания:
тем или иным способом получено, то можно построить доверительный интервал для дисперсии, аналогично тому, как мы строили его для математического ожидания:
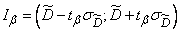 , (14.3.18)
, (14.3.18)
где величина 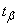 в зависимости от заданной вероятности
в зависимости от заданной вероятности 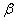 находится по таблице 14.3.1.
находится по таблице 14.3.1.
Пример 2. Найти приближенно 80%-й доверительный интервал для дисперсии случайной величины 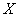 в условиях примера 1, если известно, что величина
в условиях примера 1, если известно, что величина 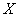 распределена по закону, близкому к нормальному.
распределена по закону, близкому к нормальному.
Решение. Величина остается той же, что в примере 1:
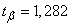 .
.
По формуле (14.3.16)
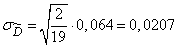 .
.
По формуле (14.3.18) находим доверительный интервал:
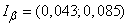 .
.
Соответствующий интервал значений среднего квадратического отклонения: 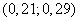 .
.
Информация, изложенная в данной статье про доверительный интервал , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое доверительный интервал, доверительная вероятность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ