Лекция
Привет, сегодня поговорим про ма тическое ожидание, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое ма тическое ожидание , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Математи́ческое ожида́ние — среднее значение случайной величины (это распределение вероятностей случайной величины, рассматривается в теории вероятностей)[1]. В англоязычной литературе обозначается через  [2] (например, от англ. Expected value или нем. Erwartungswert), в русской —
[2] (например, от англ. Expected value или нем. Erwartungswert), в русской — 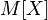 (возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение
(возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение 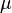 .
.
Пусть задано вероятностное пространство  и определенная на нем случайная величина
и определенная на нем случайная величина 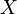 . То есть, по определению,
. То есть, по определению,  — измеримая функция. Если существует интеграл Лебега от
— измеримая функция. Если существует интеграл Лебега от 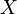 по пространству
по пространству 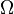 , то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается
, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается 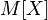 или
или  .
.
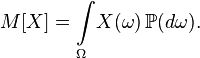
 — функция распределения случайной величины, то ее математическое ожидание задается интегралом Лебега — Стилтьеса:
— функция распределения случайной величины, то ее математическое ожидание задается интегралом Лебега — Стилтьеса: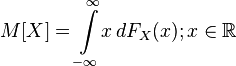 .
.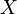 — дискретная случайная величина, имеющая распределение
— дискретная случайная величина, имеющая распределение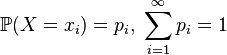 ,
,то прямо из определения интеграла Лебега следует, что
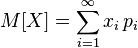 .
.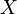 — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
— положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей 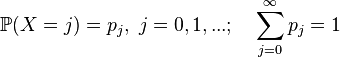
то ее математическое ожидание может быть выражено через производящую функцию последовательности 
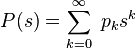
как значение первой производной в единице: 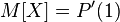 . Об этом говорит сайт https://intellect.icu . Если математическое ожидание
. Об этом говорит сайт https://intellect.icu . Если математическое ожидание 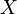 бесконечно, то
бесконечно, то 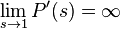 и мы будем писать
и мы будем писать 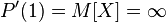
Теперь возьмем производящую функцию 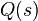 последовательности «хвостов» распределения
последовательности «хвостов» распределения 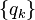
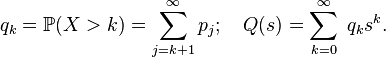
Эта производящая функция связана с определенной ранее функцией 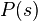 свойством:
свойством: 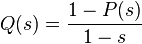 при
при 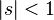 . Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
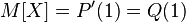
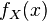 , равно
, равно .
.Пусть  — случайный вектор . Тогда по определению
— случайный вектор . Тогда по определению
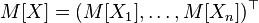 ,
,то есть математическое ожидание вектора определяется покомпонентно.
Пусть 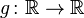 — борелевская функция , такая что случайная величина
— борелевская функция , такая что случайная величина 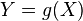 имеет конечное математическое ожидание. Тогда для него справедлива формула:
имеет конечное математическое ожидание. Тогда для него справедлива формула:
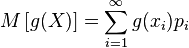 ,
,если 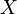 имеет дискретное распределение;
имеет дискретное распределение;
 ,
,если 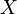 имеет абсолютно непрерывное распределение.
имеет абсолютно непрерывное распределение.
Если распределение  случайной величины
случайной величины 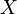 общего вида, то
общего вида, то
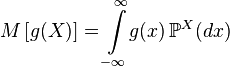 .
.В специальном случае, когда  , Математическое ожидание
, Математическое ожидание 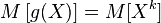 называется
называется 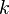 -тым моментом случайной величины.
-тым моментом случайной величины.
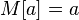
 — константа;
— константа;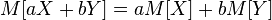 ,
, — случайные величины с конечным математическим ожиданием, а
— случайные величины с конечным математическим ожиданием, а 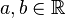 — произвольные константы;
— произвольные константы;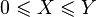 почти наверное, и
почти наверное, и  — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины
— случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины 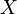 также конечно, и более того
также конечно, и более того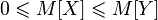 ;
; почти наверное, то
почти наверное, то .
. равно произведению их математических ожиданий
равно произведению их математических ожиданий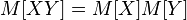 .
.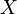 может быть выражено через ее производящую функцию моментов
может быть выражено через ее производящую функцию моментов 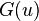 как значение первой производной в нуле:
как значение первой производной в нуле: 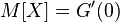
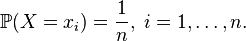 Тогда ее математическое ожидание
Тогда ее математическое ожидание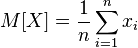
равно среднему арифметическому всех принимаемых значений.
 , где
, где 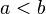 . Тогда ее плотность имеет вид
. Тогда ее плотность имеет вид 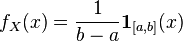 и математическое ожидание равно
и математическое ожидание равно .
.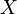 имеет стандартное распределение Коши. Тогда
имеет стандартное распределение Коши. Тогда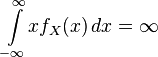 ,
,то есть математическое ожидание 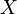 не определено.
не определено.
На этом все! Теперь вы знаете все про ма тическое ожидание, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое ма тическое ожидание и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про ма тическое ожидание
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ