5.2. Функция распределения кратко

Привет, Вы узнаете о том , что такое функция распределения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое функция распределения , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В предыдущем параграфе  мы ввели в рассмотрение ряд распределения как исчерпывающую характеристику (закон распределения) прерывной случайной величины. Однако эта характеристика не является универсальной; она существует только для прерывных случайных величин. Нетрудно убедиться, что для непрерывной случайной величины такой характеристики построить нельзя. Действительно, непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (так называемое «счетное множество»). Составить таблицу, в которой были бы перечислены все возможные значения такой случайной величины, невозможно. Кроме того, как мы увидим в дальнейшем, каждое отдельное значение непрерывной случайной величины обычно не обладает никакой отличной от нуля вероятностью. Следовательно, для непрерывной  случайной величины не существует ряда распределения в том смысле, в каком он существует для прерывной величины. Однако различные области возможных значений случайной величины все же не являются одинаково вероятными, и для непрерывной величины существует «распределение вероятностей», хотя и не в том смысле, как для прерывной.

 

Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события 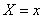, а вероятностью события 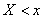, где 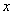 – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от 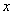, есть некоторая функция от 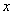. Эта функция называется функцией распределения случайной величины  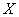и обозначается :

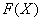.         (5.2.1)

Функцию распределения 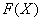 иногда называют также интегральной функцией распределения или интегральным законом распределения.

функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Сформулируем некоторые общие свойства функции распределения.

1. Функция распределения 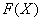 есть неубывающая функция своего аргумента, т.е. при  .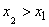

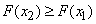2. На минус бесконечности функция распределения равна нулю:.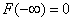

3. На плюс бесконечности функция распределения равна единице: .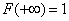

Не давая строгого доказательства этих свойств, проиллюстрируем их с помощью наглядной геометрической интерпретации. Для этого будем рассматривать случайную величину 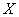 как случайную точку  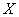на оси Ох (рис. 5.2.1), которая в результате опыта может занять то или иное положение. Тогда функция распределения  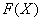есть вероятность того, что случайная точка  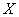в результате опыта попадет левее точки .

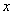Рис. Об этом говорит сайт https://intellect.icu . 5.2.1.

Будем увеличивать 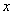, т. е. перемещать точку  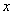вправо по оси абсцисс. Очевидно, при этом вероятность того, что случайная точка  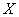попадет левее 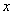, не может уменьшиться; следовательно, функция распределения  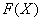с возрастанием  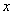убывать не может.

Чтобы убедиться  в том, что 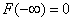, будем неограниченно перемещать точку  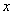влево по оси абсцисс. При этом попадание случайной точки  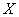левее 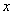 в пределе становится невозможным событием; естественно полагать, что вероятность этого события стремится к нулю, т.е. .

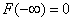Аналогичным образом, неограниченно перемещая точку 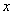 вправо, убеждаемся, что 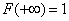, так как событие  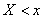становится в пределе достоверным.

График функции распределения 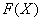 в общем случае представляет собой график неубывающей функции (рис. 5.2.2), значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрывы).

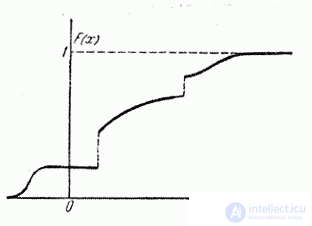
Рис. 5.2.2.

Зная ряд распределения прерывной случайной величины, можно легко построить функцию распределения этой величины. Действительно,

,

где неравенство 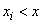 под знаком суммы указывает, что суммирование распространяется на все те значения 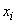, которые меньше .

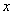Когда текущая переменная 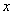 проходит через какое-нибудь из возможных значений прерывной величины 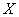, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.

Пример 1. Производится один опыт, в котором может появиться или не появиться событие 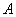. Вероятность события  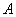равна 0,3. Случайная величина  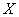– число появлений события  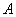в опыте (характеристическая случайная величина события 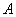). Построить ее функцию распределения.

Решение. Ряд распределения величины 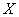 имеет вид:

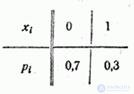
Построим функцию распределения величины :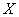

1) при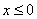 

;

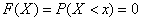2) при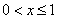 

;

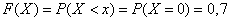3) при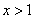 

.

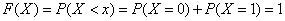График функции распределения представлен на рис. 5.2.3. В точках разрыва функция 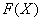 принимает значения, отмеченные на чертеже точками (функция непрерывна слева).

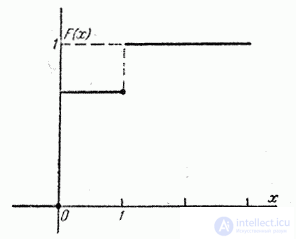
Рис. 5.2.3.

Пример 2. В условиях предыдущего примера производится 4 независимых опыта. Построить функцию распределения числа появлений события .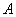

Решение. Обозначим 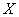 – число появлений события  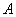в четырех опытах. Эта величина имеет ряд распределения

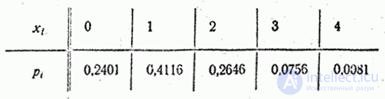
Построим функцию распределения случайной величины :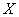

1) при  ;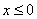

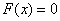2) при  ;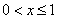

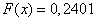3) при  ;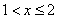

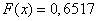4) при  ;

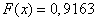5) при  ;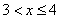

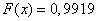6) при  .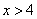

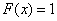График функции распределения представлен на рис. 5.2.4.

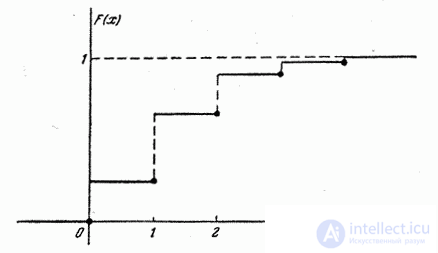
Рис. 5.2.4.

Функция распределения любой прерывной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным случайным значениям величины, и равны вероятностям этих значений. Сумма всех скачков функции 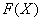 равна единице.

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними скачков становится больше, а сами скачки – меньше; ступенчатая кривая становится более плавной (рис. 5.2.5); случайна величина постепенно приближается к непрерывной величине, а ее функция распределения – к непрерывной функции (рис. 5.2.6).

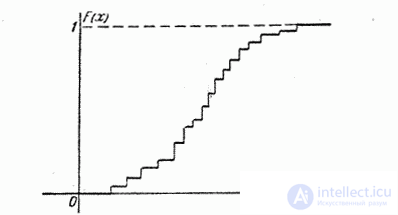
Рис. 5.2.5.

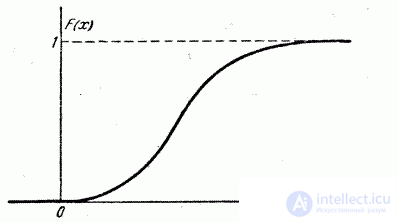
Рис. 5.2.6.

На практике обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках, как это показано на рис. 5.2.6. Однако можно построить примеры случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде является непрерывной, а в отдельных точках терпит разрыв (рис. 5.2.7).

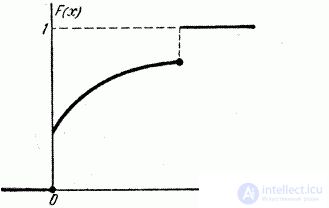
Рис. 5.2.7.

Такие случайные величины называются смешанными. В качестве примера смешанной величины можно привести площадь разрушений, наносимых цели бомбой, радиус разрушительного действия которой равен R (рис. 5.2.8).

 

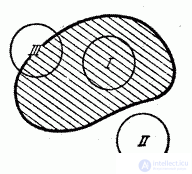
Рис. 5.2.8.

Значения этой случайной величины непрерывно заполняют промежуток от 0 до 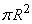, осуществляющиеся при положениях бомбы типа I и II, обладают определенной конечной вероятностью, и этим значениям соответствуют скачки функции распределения, тогда как в промежуточных значениях (положение типа III) функция распределения непрерывна. Другой пример смешанной случайной величины – время T безотказной работы прибора, испытываемого в течение времени t. Функция распределения этой случайной величины непрерывна всюду, кроме точки t.

 

 

Информация, изложенная в данной статье про функция распределения , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое функция распределения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про функция распределения