17.4. Спектральное разложение случайной функции в комплексной форме

Привет, Вы узнаете о том , что такое спектральное разложение случайной функции в комплексной форме, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое спектральное разложение случайной функции в комплексной форме , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В ряде случаев с точки зрения простоты математических преобразований оказывается удобным пользоваться не действительной, а комплексной формой записи как спектрального разложения случайной функции, так и ее характеристик: спектральной плотности и корреляционной функции. Комплексная форма записи удобна, в частности, потому, что всевозможные линейные операции над функциями, имеющими вид гармонических колебаний (дифференцирование, интегрирование, решение линейных дифференциальных уравнений и т. д.), осуществляются гораздо проще, когда эти гармонические колебания записаны не в виде синусов и косинусов, а в комплексной форме, в виде показательных функций. Комплексная форма записи корреляционной функции и спектральной плотности применяется и в тех случаях, когда сама случайная функция (а следовательно, и ее корреляционная функция и спектральная плотность) действительна.

 

Покажем, как можно в спектральном разложении случайной функции чисто формально перейти от действительной формы к комплексной.

Рассмотрим спектральное разложение (17.2.8) случайной функции 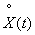 на участке :

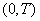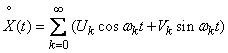,                        (17.4.1)

где 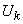,  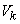- некоррелированные случайные величины, причем для каждой пары 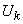,  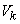с одинаковыми индексами дисперсии равны:

.

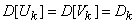Учитывая, что 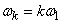; 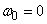, перепишем выражение (17.4.1) в виде:

.                 (17.4.2)

Придадим спектральному разложению (17.4.2) комплексную форму. Для этого воспользуемся известными формулами Эйлера:

;

.

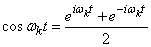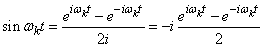Подставляя эти выражения в формулу (17.4.2), имеем:

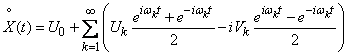,                  (17.4.3)

т. е. разложение с координатными функциями .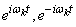

Преобразуем разложение (17.4.3) так, чтобы в нем в качестве координатных функций фигурировали только функции 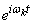, для этого распространим условно область частот  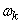на отрицательные значения  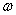и в качестве частот спектрального разложения будем рассматривать значения

        ,

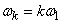
т. е. будем считать, что 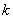 принимает не только положительные, но и отрицательные значения. Тогда формулу (17.4.3) можно переписать в виде:

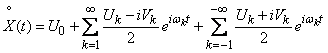,           (17.4.4)

если положить

;      .

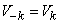Формула (17.4.4) представляет собой разложение случайной функции 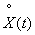, в котором в качестве координатных функций фигурируют комплексные функции 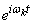, а коэффициенты представляют собой комплексные случайные величины. Обозначая эти комплексные случайные величины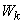  , придадим разложению (17.4.4) форму:

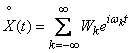,             (17.4.5)

где

                        (17.4.6)

Докажем, что разложение (17.4.5) является каноническим разложением случайной функции 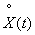. Для этого достаточно показать, что случайные коэффициенты этого разложения не коррелированы между собой.

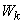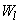Рассмотрим сначала коэффициенты двух различных членов разложения в положительной части спектра  и  при 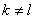, ,  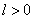и определим корреляционный момент этих величин. Согласно определению корреляционного момента для комплексных случайных величин (см.  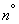15.9) имеем:

,

где 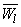 - комплексная сопряженная величина для .

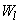При , 

,

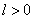
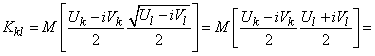
так как случайные величины 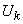, , 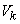фигурирующие в разложении (17.4.1), все не коррелированы между собой.

Совершенно так же докажем некоррелированность величин 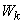,  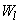при любых знаках индексов  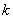и 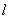, если .

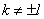Остается доказать только некоррелированность коэффициентов при симметричных членах разложения, т. Об этом говорит сайт https://intellect.icu . е. величин 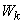 и 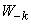 при любом 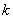. Имеем:

.

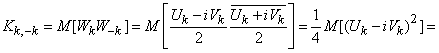
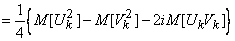Учитывая, что величины 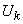, , 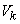входящие в один и тот же член разложения (17.4.1), не коррелированы и имеют одинаковые дисперсии 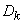, получим:

.

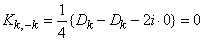Таким образом, доказано, что разложение (17.4.5) представляет собой не что иное, как каноническое разложение случайной функции 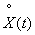 с комплексными координатными функциями  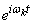и комплексными коэффициентами .

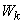Найдем дисперсии этих коэффициентов. При 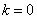 дисперсия  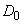осталась, очевидно, такой же, как была при действительной форме спектрального разложения. Дисперсия каждой из комплексных величин  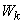(при 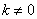) равна сумме дисперсий ее действительной и мнимой частей:

.

Введем обозначение:

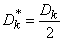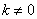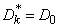 при ;   при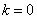 

и построим дискретный спектр случайной функции 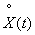, распространенный на частоты от  до  (рис. 17.4.1).

Рис. 17.4.1.

Этот спектр симметричен относительно оси ординат; от ранее построенного спектра (рис. 17.2.3) он отличается тем, что определен не только для положительных, но и для отрицательных частот, но зато его ординаты при 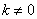 вдвое меньше соответствующих ординат прежнего спектра; сумма всех ординат по-прежнему равна дисперсии случайной функции :

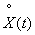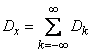.                                   (17.4.7)

Определим корреляционную функцию случайной функции 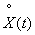, представленной в виде комплексного спектрального разложения (17.4.5). Применяя формулу (16.2.15) для корреляционной функции комплексной случайной функции, заданной каноническим разложением, имеем:

,

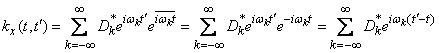или, переходя к аргументу ,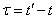

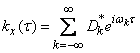,                                   (17.4.8)

где

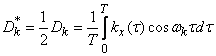     при 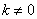.                  (17.4.9)

Придадим выражению (17.4.9) также комплексную форму. Полагая

,

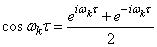получим:

.

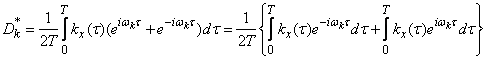Полагая во втором интеграле 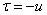, имеем:

,

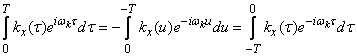откуда

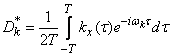.               (17.4.10)

Таким образом, мы построили комплексную форму спектрального разложения случайной функции на конечном интервале 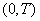). Далее естественно перейти к пределу при 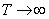, как мы делали для действительной формы, т. е. ввести в рассмотрение спектральную плотность

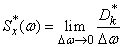
и получить в пределе из формул (17.4.8), (17.4.10) интегральные соотношения, связывающие корреляционную функцию и спектральную плотность в комплексной форме. В пределе при 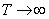 формулы (17.4.8) и (17.4.10) принимают вид:

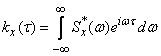,                             (17.4.11)

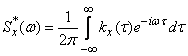.                                  (17.4.12)

Формулы (17.4.11) и (17.4.12) представляют собой комплексную форму преобразований Фурье, связывающих корреляционную функцию и спектральную плотность.

Формулы (17.4.11) и (17.4.12) могут быть и непосредственно получены из формул (17.3.9) и (17.3.10), если произвести в них замену

,

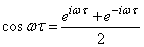положить 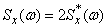 и расширить область интегрирования на интервал от  до .

Полагая в формуле (17.4.11) 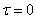, получим выражение дисперсии случайной функции :

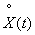.                (17.4.13)

Формула (17.4.13) выражает дисперсию случайной функции в виде суммы элементарных дисперсий, распределенных с некоторой плотностью по всему диапазону частот от  до .

Сравнивая формулу (17.4.13) и ранее выведенную (для действительной формы спектрального разложения) формулу (17.3.2), мы видим, что они различаются лишь тем, что в формуле (17.4.13) стоит несколько иная функция спектральной плотности , определенная не от 0 до , а от  до , но зато с вдвое меньшими ординатами. Если изобразить обе функции спектральной плотности на графике, они различаются только масштабом по оси ординат и тем, что функция 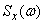 для отрицательных частот не определена (рис. 17.4.2). На практике в качестве спектральной плотности применяются как та, так и другая функции.

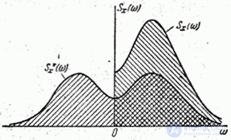
Рис. 17.4.2.

Иногда в качестве аргумента спектральной плотности рассматривают не круговую частоту (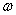), а частоту колебаний 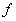, выраженную в герцах:

.

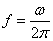В этом случае подстановкой 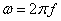 формула (17.4.11) приводится к виду:

,

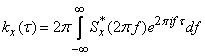или, вводя обозначение

,

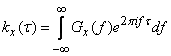.   (17.4.14)

Функция 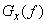 также может применяться как спектральная плотность дисперсии. Ее выражение через корреляционную функцию, очевидно, имеет вид:

.             (17.4.15)

Все приведенные нами и некоторые другие применяемые на практике выражения спектральной плотности, очевидно, отличаются друг от друга только масштабом. Каждую из них можно нормировать, деля соответствующую функцию спектральной плотности на дисперсию случайной функции.

Пример 1. Корреляционная функция случайной функции 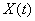 задана формулой:

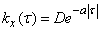,                     (17.4.16)

где 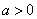 (рис. 17.4.3).

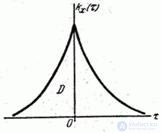
Рис. 17.4.3.

Пользуясь комплексной формой преобразования Фурье, определить спектральную плотность .

Решение. По формуле (17.4.12) находим:

.

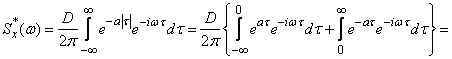
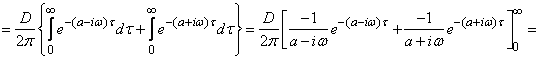
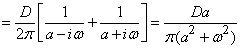График спектральной плотности

представлен на рис. 17.4.4.

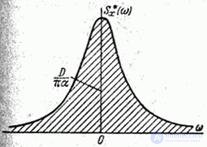
Рис. 17.4.4.

Посмотрим, как будут вести себя корреляционная функция и спектральная плотность при изменении .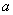

При уменьшении 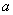 корреляционная функция будет убывать медленнее; характер изменения случайной функции становится более плавным; соответственно в спектре случайной функции больший удельный вес приобретают малые частоты: кривая спектральной плотности вытягивается вверх, одновременно сжимаясь с боков; в пределе при  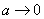случайная функция выродится в обычную случайную величину с дискретным спектром, состоящим из единственной линии с частотой .

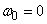При увеличении 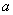 корреляционная функция убывает быстрее, характер колебаний случайной функции становится более резким и беспорядочным; соответственно этому в спектре случайной функции преобладание малых частот становится все менее выраженным; при  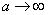спектр случайной функции приближается к равномерному (так называемому «белому») спектру, в котором нет преобладания каких-либо частот.

Пример 2. Нормированная корреляционная функция случайной функции 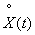 имеет вид:

(рис. 17.4.5).

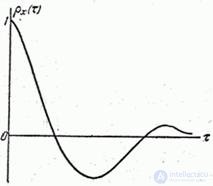
Рис. 17.4.5.

Определить нормированную спектральную плотность.

Решение. Представляем 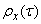 в комплексной форме:

.

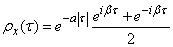Нормированную спектральную плотность 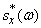 находим по формуле (17.4.12), подставляя в нее  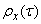вместо :

,

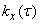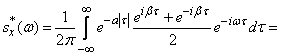
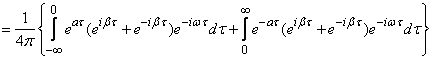откуда после элементарных преобразований получаем:

.

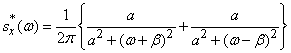Вид графика спектральной плотности зависит от соотношения параметров 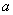 и 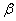, т. е. от того, что преобладает в корреляционной функции: убывание по закону  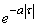или колебание по закону 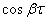. Очевидно, при сравнительно малых  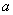преобладает колебание, при сравнительно больших  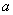- убывание. В первом случае случайная функция близка к периодическим колебаниям частоты  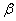со случайной амплитудой и фазой; соответственно в спектре случайной функции преобладают частоты, близкие к частоте 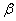. Во втором случае спектральный состав случайной функции более равномерен, преобладания тех иле иных частот не наблюдается; в пределе при  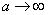спектр случайной функции приближается к «белому» спектру.

В качестве иллюстрации на рис. 17.4.6 изображены нормированные спектральные плотности для случаев:

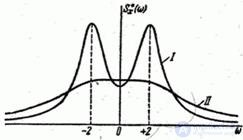
Рис. 17.4.6.

1) 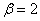,  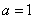(кривая ); 2) 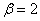,  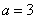(кривая 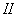). Как видно из чертежа, при  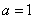спектр случайной функции обнаруживает ярко выраженный максимум в области частот 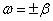. При 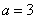 (кривая 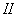) спектральная плотность в значительном диапазоне частот остается почти постоянной.

 

Информация, изложенная в данной статье про спектральное разложение случайной функции в комплексной форме , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое спектральное разложение случайной функции в комплексной форме и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ