2.2. Непосредственный подсчет вероятностей кратко

Привет, Вы узнаете о том , что такое непосредственный подсчет вероятностей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое непосредственный подсчет вероятностей , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Существует целый класс опытов, для которых вероятности их возможных исходов легко оценить непосредственно из условий самого опыта. Для этого нужно, чтобы различные исходы опыта обладали симметрией и в силу этого были объективно одинаково возможными.

 

Рассмотрим, например, опыт, состоящий в бросании игральной кости, т.е. симметричного кубика, на гранях которого нанесено различное число очков: от 1 до 6.

В силу симметрии кубика есть основания считать все шесть возможных исходов опыта одинаково возможными. Именно это дает нам право предполагать, что при многократном бросании кости все шесть граней будут выпадать примерно одинаково часто. Это предположение для правильно выполненной кости действительно оправдывается на опыте; при многократном бросании кости каждая ее грань появляется примерно в одной шестой доле всех случаев бросания, причем отклонение этой доли от 1/6 тем меньше, чем большее число опытов произведено. Имея в виду, что вероятность достоверного события принята равной единице, естественно приписать выпадению каждой отдельной грани вероятность, равную 1/6. Это число характеризует некоторые объективные свойства данного случайного явления, а именно свойство симметрии шести возможных исходов опыта.

Для всякого опыта, в котором возможные исходы симметричны и одинаково возможны, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей.

Симметричность возможных исходов опыта обычно наблюдается только в искусственно организованных опытах, типа азартных игр. Так как первоначальное развитие теория вероятностей получила именно на схемах азартных игр, то прием непосредственного подсчета вероятностей, исторически возникший вместе с возникновением математической теории случайных явлений, долгое время считался основным и был положен в основу так называемой «классической» теории вероятностей. При этом опыты, не обладающие симметрией возможных исходов, искусственно сводились к «классической» схеме.

Несмотря на ограниченную сферу практических применений этой схемы, она все же представляет известный интерес, так как именно на опытах, обладающих симметрией возможных исходов, и на событиях, связанных с такими опытами, легче всего познакомиться с основными свойствами вероятностей. Такого рода событиями, допускающими непосредственный подсчет вероятностей , мы и займемся в первую очередь.

Предварительно введем некоторые вспомогательные понятия.

1. Полная группа событий.

Говорят, что несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.

Примеры событий, образующих полную группу:

1) выпадение герба и выпадение цифры при бросании монеты;

2) попадание и промах при выстреле;

3) появление 1,2,3,4,5,6 очков при бросании игральной кости;

4) появление белого шара и появление черного шара при вынимании одного шара из урны, в которой 2 белых и 3 черных шара;

5) ни одной опечатки, одна, две, три и более трех опечаток при проверке страницы напечатанного текста;

6) хотя бы одно попадание и хотя бы один промах при двух выстрелах.

2. Несовместимые события.

Несколько событий называют несовместимыми в данном опыте, если никакие два из них не могут появиться вместе.

Примеры несовместимых событий:

1) выпадение герба и выпадение цифры при бросании монеты;

2) попадание и промах при выстреле;

3) появление 1,3, 4 очков при одном бросании игральной кости;

4) ровно один отказ, ровно два отказа, ровно три отказа технического устройства за десять часов работы.

3. Об этом говорит сайт https://intellect.icu . Равновозможные события.

Несколько событий в данном опыте называются равновозможными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое.

Примеры равновозможных событий:

1) выпадение герба и выпадение цифры при бросании монеты;

2) появление 1,3, 4, 5 очков при бросании игральной кости;

3) появление карты бубновой, червонной, трефовой масти при вынимании карты из колоды;

4) появление шара с №1, 2, 3 при вынимании одного шара из урны, содержащей 10 перенумерованных шаров.

Существуют группы событий, обладающие всеми тремя свойствами: они образуют полную группу, несовместимы и равновозможны; например: появление герба и цифры при бросании монеты; появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости. События, образующие такую группу, называются случаями (иначе «шансами»).

Если какой-либо опыт по своей структуре обладает симметрией возможных исходов, то случаи представляют собой исчерпывающую систему равновозможных и исключающих друг друга исходов опыта. Про такой опыт говорят, что он «сводится к схеме случаев» (иначе – к «схеме урн»).

Схема случаев по преимуществу имеет место в искусственно организованных опытах, в которых заранее и сознательно обеспечена одинаковая возможность исходов опыта (как, например, в азартных играх). Для таких опытов возможен непосредственный подсчет вероятностей, основанный на оценке доли так называемых «благоприятных» случаев в общем числе случаев.

Случай называется благоприятным (или «благоприятствующим») некоторому событию, если появление этого случая влечет за собой появление данного события.

Например, при бросании игральной кости возможны шесть случаев: появление 1, 2, 3, 4, 5, 6 очков. Из них событию  – появлению четного числа очков – благоприятны три случая: 2, 4, 6 и не благоприятны остальные три.

Если опыт сводится к схеме случаев, то вероятность события  в данном опыте можно оценить по относительной доле благоприятных случаев. Вероятность события  вычисляется как отношение числа благоприятных случаев к общему числу случаев:

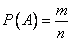,        (2.2.1)

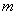где Р(А) – вероятность события ;  – общее число случаев; – число случаев, благоприятных событию .

Так как число благоприятных случаев всегда заключено между 0 и  (0 – для невозможного и – для достоверного события), то вероятность события, вычисленная по формуле (2.2.1), всегда есть рациональная правильная дробь:

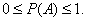      (2.2.2)

Формула (2.2.1), так называемая «классическая формула» для вычисления вероятностей, долгое время фигурировала в литературе как определение вероятности. В настоящее время при определении (пояснении) вероятности обычно исходят из других принципов, непосредственно связывая понятие вероятности с эмпирическим понятием частоты; формула же (2.2.1) сохраняется лишь как формула для непосредственного подсчета вероятностей, пригодная тогда и только тогда, когда опыт сводится к схеме случаев, т.е. обладает симметрией возможных исходов.

Пример 1. В урне находится 2 белых и 3 черных шара. Из урны наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет белым.

Решение. Обозначим  событие, состоящее в появлении белого шара. Общее число случаев 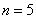; число случаев, благоприятных событию, 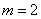. Следовательно,

.

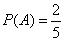Пример 2. В урне a белых и b черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение. Обозначим 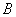 событие, состоящее в появлении двух белых шаров. Подсчитаем общее число возможных случаев и число случаев 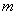, благоприятных событию :

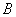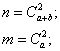
следовательно,

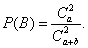
Пример 3. В партии из 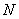 изделий  бракованных. Из партии выбирается наугад  изделий. Определить вероятность того, что среди этих n изделий будет ровно 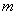 бракованных.

Решение. Общее число случаев, очевидно, равно 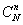, число благоприятных случаев 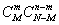, откуда вероятность интересующего нас события

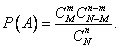
Информация, изложенная в данной статье про непосредственный подсчет вероятностей , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое непосредственный подсчет вероятностей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про непосредственный подсчет вероятностей