11.4. Уточнение результатов, полученных методом линеаризации кратко

Привет, Вы узнаете о том , что такое уточнение результатов полученных методом линеаризации, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое уточнение результатов полученных методом линеаризации , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В некоторых задачах практики возникает сомнение в применимости метода линеаризации в связи с тем, что диапазон изменений случайных аргументов не настолько мал, чтобы в его пределах функция могла быть с достаточной точностью линеаризована.

 

В этих случаях для проверка применимости метода линеаризации и для уточнения полученных результатов может быть применен метод, основанный на сохранении в разложении функции не только линейных членов, но и некоторых последующих членов более высоких порядков и оценке погрешностей, связанных с этими членами.

Для того чтобы пояснить этот метод, рассмотрим сначала наиболее простой случай функции одного случайного аргумента. Случайная величина 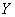 есть функция случайного аргумента :

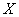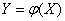,                              (11.4.1)

причем функция 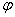 сравнительно мало отличается от линейной на ветке практически возможных значений аргумента 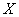, но все же отличается настолько, что возникает сомнение в применимости метода линеаризации. Для проверки этого обстоятельства применим более точный метод, а именно: разложим функцию  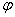в ряд Тейлора в окрестности точки  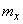и сохраним в разложении первые три члена:

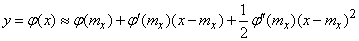.               (11.4.2)

Та же формула будет, очевидно, приближенно связывать случайные величины 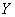 и :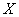

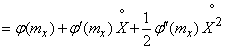.             (11.4.3)

Пользуясь выражением (11.4.3), найдем математическое ожидание и дисперсию величины 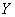. Применяя теоремы о числовых характеристиках, имеем:

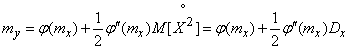.                  (11.4.4)

По формуле (11.4.4) можно найти уточненное значение математического ожидания и сравнить его с тем значением 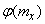, которое получается методом линеаризации; поправкой, учитывающей нелинейность функции, является второй член формулы (11.4.4).

Определяя дисперсию правой и левой части формулы (11.4.3), имеем:

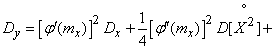
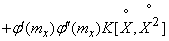,                (11.4.5)

где 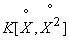 - корреляционный момент величин .

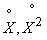Выразим входящие в формулу (11.4.5) величины через центральные моменты величины :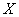

,

.

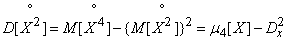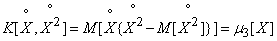Окончательно имеем:

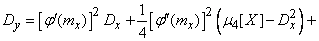
.                      (11.4.6)

Формула (11.4.6) дает уточненное значение дисперсии по сравнению с методом линеаризации; ее второй и третий члены представляют собой поправку на нелинейность функции. Об этом говорит сайт https://intellect.icu . В формулу, кроме дисперсии аргумента 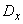, входят еще третий и четвертый центральные моменты , 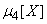. Если эти моменты известны, то поправка к дисперсии может быть найдена непосредственно по формуле (11.4.6). Однако зачастую нет необходимости в ее точном определении; достаточно лишь знать ее порядок. На практике часто встречаются случайные величины, распределенные приблизительно по нормальному закону. Для случайной величины, подчиненной нормальному закону,

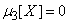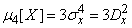, ,                 (11.4.7)

и формула (11.4.6) принимает вид:

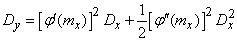.          (11.4.8)

Формулой (11.4.8) можно пользоваться для приближенной оценки погрешности метода линеаризации в случае, когда аргумент распределен по закону, близкому к нормальному.

Совершенно аналогичный метод может быть применен по отношению к функции нескольких случайных аргументов:

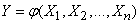.                       (11.4.9)

Разлагая функцию

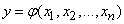
в ряд Тейлора в окрестности точки  и сохраняя в разложении члены не выше второго порядка, имеем приближенно:

,

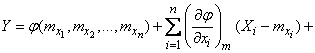
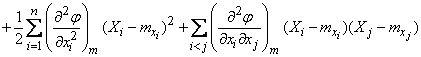или, вводя центрированные величины,

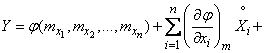
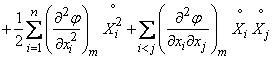, (11.4.10)

где индекс 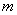 по-прежнему обозначает, что в выражение частной производной вместо аргументов  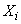подставлены их математические ожидания .

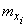Применяя к формуле (11.4.10) операцию математического ожидания, имеем:

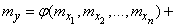
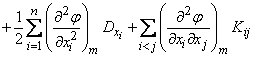,                 (11.4.11)

где 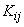 - корреляционный момент величин .

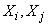В наиболее важном для практики случае, когда аргументы 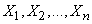 некоррелированны, формула (11.4.11) принимает вид:

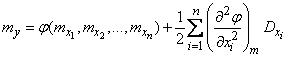.                     (11.4.12)

Второй член формулы (11.4.12) представляет собой поправку на нелинейность функции.

Перейдем к определению дисперсии величины 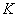. Чтобы получить выражение дисперсии в наиболее простом виде, предположим, что величины  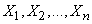не только некоррелированны, но и независимы. Определяя дисперсию правой и левой части (11.4.10) и пользуясь теоремой о дисперсии произведения (см.  10.2), получим:

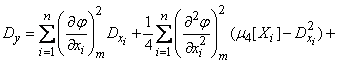
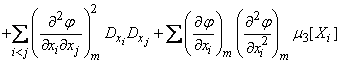.                    (11.4.13)

Для величин, распределенных по закону, близкому к нормальному, можно воспользоваться формулой (11.4.7) и преобразовать выражение (11.4.13) к виду:

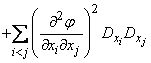.                    (11.4.14)

Последние два члена в выражении (11.4.14) представляют собой «поправку на нелинейность функции» и могут служить для оценки точности метода линеаризации при вычислении дисперсии.

 

 

Информация, изложенная в данной статье про уточнение результатов полученных методом линеаризации , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое уточнение результатов полученных методом линеаризации и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про уточнение результатов полученных методом линеаризации