17.7. Эргодическое свойство стационарных случайных функций кратко

Привет, Вы узнаете о том , что такое эргодическое свойство стационарных случайных функций, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое эргодическое свойство стационарных случайных функций , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Рассмотрим некоторую стационарную случайную функцию 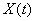 и предположим, что требуется оценить ее характеристики: математическое ожидание  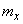и корреляционную функцию 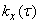. Выше (см.  15.4) были изложены способы получения этих характеристик из опыта. Для этого нужно располагать известным числом реализаций случайной функции 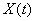. Обрабатывая эти реализации, можно найти оценки для математического ожидания  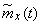и корреляционной функции 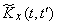. В связи с ограниченностью числа наблюдений (функция  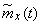не будет строго постоянной; ее придется осреднить и заменить некоторым постоянным 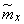; аналогично, осредняя значения  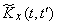для разных 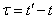, получим корреляционную функцию .

 

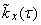Этот метод обработки, очевидно, является довольно сложным и громоздким и к тому же состоит из двух этапов: приближенного определения характеристик случайной функции и также приближенного осреднения этих характеристик. Естественно возникает вопрос: нельзя ли для стационарной случайной функции этот сложный, двухступенчатый процесс обработки заменить более простым, который заранее базируется на предположении, что математическое ожидание не зависит от времени, а корреляционная функция - от начала отсчета?

Кроме того, возникает вопрос: при обработке наблюдений над стационарной случайной функцией является ли существенно необходимым располагать несколькими реализациями? Поскольку случайный процесс является стационарным и протекает однородно по времени, естественно предположить, что одна-единственная реализация достаточной продолжительности может служить достаточным опытным материалом для получения характеристик случайной функции.

При более подробном рассмотрении этого вопроса оказывается, что такая возможность существует не для всех случайных процессов: не всегда одна реализация достаточной продолжительности оказывается эквивалентной множеству отдельных реализаций.

Для примера рассмотрим две стационарные случайные функци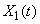и  и , представленные совокупностью своих реализаций на рис. 17.7.1 и 17.7.2.

Рис. 17.7.1.

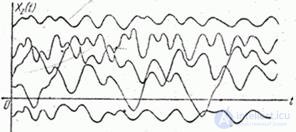
Рис. 17.7.2.

Для случайной функции  характерна следующая особенность: каждая из ее реализаций обладает одними и теми же характерными признаками: средним значением, вокруг которого происходят колебания, и средним размахом этих колебаний. Выберем произвольно одну из таких реализаций и продолжим мысленно опыт, в результате которого она получена, на некоторый участок времени 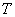. Очевидно, при достаточно большом  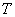эта одна реализация сможет дать нам достаточно хорошее представление о свойствах случайной функции в целом. В частности, осредняя значения этой реализации вдоль оси абсцисс - по времени, мы должны получить приближенное значение математического ожидания случайной функции; осредняя квадраты отклонений от этого среднего, мы должны получить приближенное значение дисперсии, и т. Об этом говорит сайт https://intellect.icu . д.

Про такую случайную функцию говорят, что она обладает эргодическим свойством. Эргодическое свойство состоит в том, что каждая отдельная реализация случайной функции является как бы «полномочным представителем» всей совокупности возможных реализаций; одна реализация достаточной продолжительности может заменить при обработке множество реализаций той же общей продолжительности.

Рассмотрим теперь случайную функцию 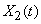. Выберем произвольно одну из ее реализаций, продолжим ее мысленно на достаточно большой участок времени и вычислим ее среднее значение по времени на всем участке наблюдения. Очевидно, это среднее значение для каждой реализации будет свое и может существенно отличаться от математического ожидания случайной функции, построенного как среднее из множества реализаций. Про такую случайную функцию говорят, что она не обладает эргодическим свойством.

Если случайная функция 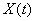 обладает эргодическим свойством, то для нее среднее по времени (на достаточно большом участке наблюдения) приближенно равно среднему по множеству наблюдений. То же будет верно и для 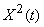,  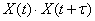и т. д. Следовательно, все характеристики случайной функции (математическое ожидание, дисперсию, корреляционную функцию) можно будет приближенно определять по одной достаточно длинной реализации.

Какие же стационарные случайные функции обладают, а какие не обладают эргодическим свойством?

Поясним этот вопрос наглядно, исходя из примера. Рассмотрим случайную функцию 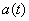 - колебания угла атаки самолета на установившемся режиме горизонтального полета. Предположим, что подлет происходит в каких-то типичных средних метеорологических условиях. Колебания угла атаки вызваны случайными возмущениями, связанными с турбулентностью атмосферы. Среднее значение угла атаки, около которого происходят колебания, зависит от высоты полета 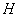. Зависит от этой высоты и размах колебаний: известно, что в нижних слоях атмосферы турбулентность сказывается сильнее, чем в верхних.

Рассмотрим случайную функцию 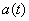 - колебания угла атаки на заданной высоте 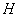. Каждая из реализаций этой случайной функции осуществляется в результате воздействия одной и той же группы случайных факторов и обладает одними и теми же вероятностными характеристиками; случайная функция  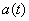обладает эргодическим свойством (рис. 17.7.3).

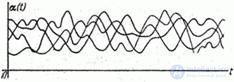
Рис. 17.7.3.

Представим себе теперь, что рассматривается случайная функция 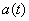 не для одной высоты 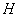, а для целого диапазона, внутри которого задан какой-то закон распределения высот (например, закон равномерной плотности). Такая случайная функция, оставаясь стационарной, очевидно, уже не будет обладать эргодическим свойством; ее возможные реализации, осуществляющиеся с какими-то вероятностями, имеют различный характер (рис. 17.7.4).

Рис. 17.7.4.

Для этого случайного процесса характерно то, что он как бы «разложим» на более элементарные случайные процессы; каждый из них осуществляется с некоторой вероятностью и имеет свои индивидуальные характеристики. Таким образом, разложимость, внутренняя неоднородность случайного процесса, протекающего с некоторой вероятностью по тому или другому типу, есть физическая причина неэргодичности этого процесса.

В частности, неэргодичность случайного процесса может быть связана с наличием в его составе слагаемого в виде обычной случайной величины (т. е. наличие в спектре случайного процесса, помимо непрерывной части, конечной дисперсии при частоте 0).

Действительно, рассмотрим случайную функцию

,                                (17.7.1)

где 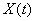 - эргодическая стационарная случайная функция с характеристиками 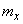, 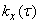;  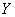- случайная величина с характеристикам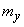и  и ; предположим к тому же, что 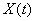 и 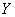 некоррелированны.

Определим характеристики случайной функции 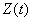. Согласно общим правилам сложения случайных функций (см.  15.8) имеем:

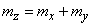,                       (17.7.2)

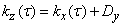.    (17.7.3)

Из формул (17.7.2) и (17.7.3) видно, что случайная функция 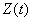 является стационарной. Но обладает ли она эргодическим свойством? Очевидно, нет. Каждая ее реализация будет по характеру отличаться от других, будет обладать тем или иным средним по времени значением в зависимости от того, какое значение приняла случайная величина  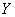(рис. 17.7.5).

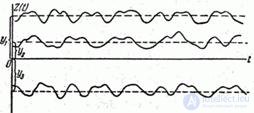
Рис. 17.7.5.

Об эргодичности или неэргодичности случайного процесса может непосредственно свидетельствовать вид его корреляционной функции. Действительно, рассмотрим корреляционную функцию неэргодической случайной функции (17.7.1). Она отличается от корреляционной функции случайной функции 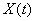 наличием постоянного слагаемого (рис. 17.7.6).

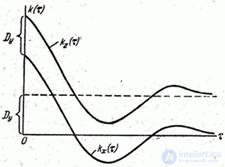
Рис. 17.7.6.

В то время как корреляционная функция 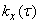 стремится к нулю при  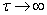(корреляционная связь между значениями случайной функции неограниченно убывает по мере увеличения расстояния между ними), функция  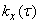уже не стремится к нулю при 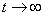, а приближается к постоянному значению .

На практике мы не имеем возможности исследовать случайный процесс и его корреляционную функцию на бесконечном участке времени; участок значений 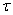, с которым мы имеем дело, всегда ограничен. Если при этом корреляционная функция стационарного случайного процесса при увеличении  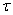не убывает, а, начиная с некоторого 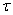, остается приблизительно постоянной, это обычно есть признак того, что в составе случайной функции имеется слагаемое в виде обычной случайной величины и что процесс не является эргодическим. Стремление же корреляционной функции к нулю при  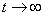говорит в пользу эргодичности процесса. Во всяком случае оно достаточно для того, чтобы математическое ожидание функции можно было определять как среднее по времени.

При решении практических задач часто суждение об эргодичности случайного процесса выносится не на основе исследования поведения корреляционной функции при 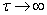, а на основании физических соображений, связанных с существом процесса (его предположительной «разложимостью» или «неразложимостью» на элементарные процессы различного типа, появляющиеся с некоторыми вероятностями).

Информация, изложенная в данной статье про эргодическое свойство стационарных случайных функций , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое эргодическое свойство стационарных случайных функций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про эргодическое свойство стационарных случайных функций