Геометрическая вероятность, Игла Буффона (буйвола) кратко

Привет, Вы узнаете о том , что такое геометрическая вероятность, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое геометрическая вероятность, игла буффона , игла буйвола, интегральная геометрия, стохастическая геометрия , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

геометрическая вероятность - это понятие вероятности, что вводится так: пусть - некоторое подмножество прямой, плоскости или пространства. случайное событие - подмножество . Тогда вероятность случайного события определяется формулой: где - длина, площадь или объем множеств и .

Это связано с интерпретацией вероятности как меры на выбранном пространстве элементарных событий . В данном случае он совпадает с евклидовым пространством .

Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие A – это подмножество этой области, пространства элементарных исходов G.

Если для простоты считать, что все точки G «равноправны» (выбор точек равномерен внутри области), то вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.

Геометрическая вероятность события А определяется отношением:

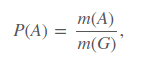
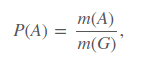
где m(G) , m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов GG и события АА соответственно.

Чаще всего, в одномерном случае речь будет идти о длинах отрезков, в двумерном - о площадях фигур, в трехмерном - об объемах тел.

Основная сложность при решении задач такого типа - построить математическую модель эксперимента, нужным образом выбрать пространство элементарных исходов, обозначить событие, выразить его математически как некоторую область. К сожалению, единого рецепта решения подобых заданий нет, нужно "набить" руку на разных задачах

Использование геометрической вероятности

• Игла Бюффона : Какова вероятность того, что игла брошена на поверхность разграфленную параллельными прямыми расположенными через равные промежутки пересечет одну из этих прямых?
• Парадокс Бертрана : Какое матсподивання длины случайно выбранной хорды на единичной окружности?
• Какова вероятность того, что три случайно выбранные на плоскости точки формируют остроугольные треугольник?
• И подобные

Задачи следующего типа и методы их решения были впервые изучены в 18 веке, и общая тема стала известна как геометрическая вероятность .

• ( игла буффона ) Какова вероятность того, что игла, случайно упавшая на пол, отмеченный одинаковыми параллельными линиями, пересечет одну из линий?

• Какова средняя длина случайной хорды единичного круга? (ср . парадокс Бертрана ).
• Какова вероятность того, что три случайные точки на плоскости образуют острый (а не тупой) треугольник?
• Какова средняя площадь полигональных областей, образующихся при распределении по плоскости произвольно ориентированных линий?

Для математического развития см. Краткую монографию Соломона.

В конце ХХ века тема разделилась на две темы с разными акцентами: интегральная геометрия и стохастическая геометрия .

Интегральная геометрия возникла из того принципа, что математически естественные вероятностные модели - это те, которые инвариантны относительно определенных групп преобразований. В этой теме особое внимание уделяется систематической разработке формул для расчета ожидаемых значений, связанных с геометрическими объектами, полученными из случайных точек, и отчасти их можно рассматривать как сложную ветвь многомерного исчисления .

Стохастическая геометрия подчеркивает сами случайные геометрические объекты. Например: разные модели для случайных линий или для случайных мозаик плоскости; случайные множества, образованные путем создания точек пространственного пуассоновского процесса быть (скажем) центрами дисков.

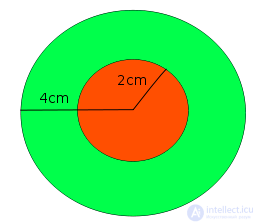
Простое геометрическое вероятностное решение : если вы выстрелите стрелой наугад, какова вероятность остаться в маленьком круге? Площадь большого круга равна π4 ² = 50,26 см ^2, а площадь π2 ² = 12,56 см ^{2 - площадь} малого круга. Таким образом, вероятность попасть в маленький круг , который может произойти в любой момент, составляет 12,56 / 50,26 = 0,25.

Примеры

игла буйвола

В пределах круга выше случайно выбранные точки, попадающие в центральную область, зависят только от областей областей круга. Об этом говорит сайт https://intellect.icu . Радиус самого большого круга составляет 4 сантиметра, а радиус центрального круга - всего 2 сантиметра. Площадь круга рассчитывается, поэтому размер большого круга и маленький . Тогда запрашиваемая вероятность равна

Нарезание нитки метровой длины за цикл ножницами можно превратить в геометрическую задачу, если предположить, что точка разреза выбрана случайным образом. Первоначально веревку можно представить как выпрямленную на линии чтения, позволяющую ей осесть в диапазоне чтения.. Когда струна обрезается в выбранной точке, получаются два отрезка бечевки. В строке чтения они соответствуют интервалам а также с длиной а также . Расчеты вероятности можно уменьшить, перечислив благоприятные числазначения как совместные длины зазоров и сравнение их с общей длиной строки (которая равна единице).

Иголка Buffalo - это проблема, когда игла или спичка брошены на пол. Какова вероятность того, что Нейла пробьет брешь в полу? Проблема может быть сведена к задаче с двумя параметрами: центром палки и положением палки относительно щелей пола.

Формально

Стохастический эксперимент заключается в выборе наугад точки из множества. По его математическую модель принято рассматривать вероятностное пространство , где - борелева множество из, - класс борелевих подмножеств множества , - вероятность на классе, Которая для каждого из этого класса определяется равенством:

,

где - мера Лебега на (значение на параллелепипедах равна ).

Так определенную вероятность назовем геометрической (понятно, что множество должно удовлетворять условие .

Примеры решений на геометрическую вероятность

Пример. На плоскость, разграфленную параллельными полосами шириной 2d , расстояние между осевыми линиями которых равно 2D2D, наудачу брошен круг радиуса rr (r+d<D ). Найти вероятность того, что круг пересечет некоторую полосу.

Решение. В качестве элементарного исхода этого испытания будем считать расстояние xx от центра круга до осевой линии ближайшей к кругу полосы (ее обозначим за 0). Тогда все пространство элементарных исходов – это отрезок, равный половине расстояния между осями полос G={x:0≤x≤D} . Его мера - это длина отрезка, то есть m(G)=Dm(G)=D.

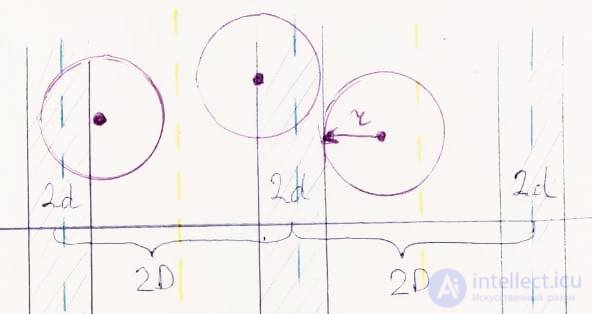
Рассмотрим теперь случаи, благоприятствующие событию AA = (Круг пересечет полосу), и найдем меру соответствующей области точек. На чертеже выше покажем различные варианты выпадения круга.

Пересечение круга с полосой очевидно произойдет в том случае, если его центр попадет в полосу (точнее, ее половину), т.е. координата центра круга удовлетворяет неравенству 0≤x≤d , длина этого отрезка dd.

Также круг пересечет полосу, если его центр будет находится от края полосы на расстоянии меньшем чем радиус (если равен радиусу - круг коснется полосы, если больше - то отстоит от полосы), т.е. когда d≤x≤d+r (длина этого отрезка r ).

Тогда вероятность события AA по геометрическому определению вероятности:

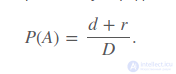
Пример. Два человека договорились встретиться в определенном месте от 17 до 18 часов. При этом каждый обязался после прихода на место встречи ожидать другого 30 минут. Какова вероятность встречи этих людей, если каждый из них равновозможно придет в течение указанного интервала времени?

Решение. Обозначим моменты прихода первого и второго человека за x и y . Так как они приходят в промежуток длительности 60 минут (от 17 до 18 часов), то справедливы следующие условия: 0≤x≤60 и 0≤y≤60 .

Рассмотрим прямоугольную систему координат xOy В этой системе координат всем возможным значениям времени прихода людей соответствуют точки квадрата со стороной 60.

Лица встретятся, если один человек придет раньше, чем уйдет другой, то есть если y<x+30 , когда y>x (второй пришел позже первого, но не позже чем через 30 минут от него) и x<y+30 , когда y<xy

Более компактно запишем условия

x<y<x+30 или x−30<y<x.(∗)

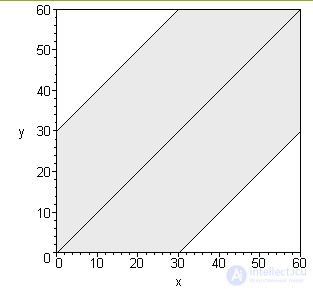
Построим прямые y=x , y=x−30 , y=x+30 и закрасим область, лежащую внутри квадрата, точки которой удовлетворяют условиям (*). Точки этой фигуры (серый шестиугольник в центре) являются благоприятствующими событию AA =(люди встретятся).

Тогда искомая вероятность встречи по геометрическому определению вероятности равна отношению площади этой фигуры к площади квадрата:

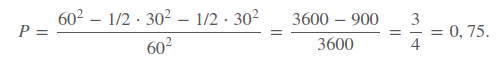
Исследование, описанное в статье про геометрическая вероятность, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое геометрическая вероятность, игла буффона , игла буйвола, интегральная геометрия, стохастическая геометрия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ