Лекция
Привет, Вы узнаете о том , что такое Парадокс Симпсона в статистике с примерами, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Парадокс Симпсона в статистике с примерами , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Радует, когда на диаграмме кроме новых созвездий находится нечто похожее на зависимость. В таком случае мы строим модель, которая хорошо объясняет связь между двумя переменными. Но исследователь должен понимать не только, как работать с данными, но и какая история из реального мира за ними лежит. В противном случае легко сделать ошибку. Расскажу о парадоксе Симпсона — одном из самых опасных примеров обманчивых данных, который может перевернуть связь с ног на голову.
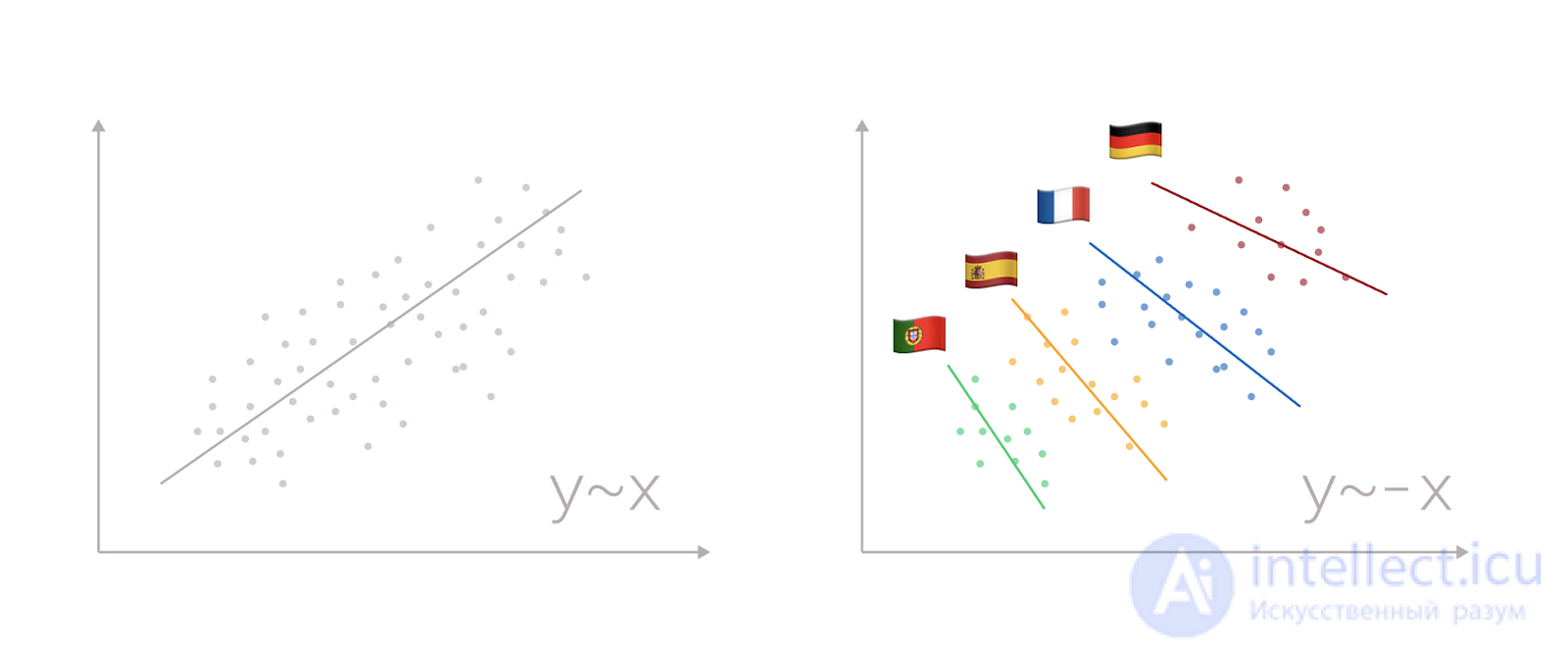
Посмотрим на две условные переменные X и Y. Построив диаграмму, мы увидим облако, явно вытянутое из левого нижнего угла в правый верхний, как на рисунке выше. В такую картинку идеально вписывается линейная регрессия, которая с относительно низкой ошибкой поможет нам предсказать значения: чем больше X, тем больше Y. Задача выполнена. На первый взгляд.
Более опытный коллега порекомендует нам добавить на диаграмму разбиение по когортам: например, по странам. Последовав его совету, мы увидим, что связь действительно есть, но она диаметрально противоположная — в рамках отдельно взятой страны чем больше X, тем меньше Y.
Это и есть парадокс Симпсона: явление, при котором объединение нескольких групп данных с одинаково направленной зависимостью приводит к изменению направления на противоположное.
Самый известный пример парадокса Симпсона в реальном мире — это неразбериха с половой дискриминацией при приеме в университет Беркли в 1973 году. Среди исследователей ходит байка о том, что университет даже судили, однако в интернете не найти убедительных свидетельств судебного разбирательства.
Так выглядит статистика приема университета за 1973 год:
| Пол | Заявки | Принято |
| Мужчины | 8442 | 3738 (44%) |
| Женщины | 4321 | 1494 (35%) |
Разница значительная. Слишком большая, чтобы быть случайной.
Однако если разбить данные по факультетам, картина меняется. Исследователи выяснили, что причина разницы в том, что женщины подавали заявки на направления с более жестким конкурсом. К тому же было обнаружено, что 6 из 85 факультетов имели дискриминацию в пользу женщин, и только 4 — против.
Разница возникает исключительно из-за разницы в размерах выборок и размере конкурса между факультетами. Покажу на примере двух факультетов.
| Фаультет | Пол | Заявки | Принято |
| A | Мужчины | 400 | 200 (50%) |
| A | Женщины | 200 | 100 (50%) |
| B | Мужчины | 150 | 50 (33%) |
| B | Женщины | 450 | 150 (33%) |
| Итого | Мужчины | 550 | 250 (45%) |
| Итого | Женщины | 650 | 250 (38%) |
Оба факультета принимают одинаковые доли женщин и мужчин. Об этом говорит сайт https://intellect.icu . Однако поскольку абсолютное количество мужчин было больше на факультете с более высоким процентом принятых, если объединить данные, получится, что в целом процент поступления мужчин выше.
Представьте, что вы проводите A/B эксперимент для повышения конверсии вашего лендинга. Эксперимент проводится два дня, но в первый день сломался распределитель посетителей, и вариант B получил больше посетителей. Во второй день эта проблема была устранена. В результате получились следующие цифры:
| A | B | |||
| Посетители | Конверсии | Посетители | Конверсии | |
| День 1 | 400 | 30 (7.5%) | 2000 | 140 (7%) |
| День 2 | 1000 | 60 (6.0%) | 1000 | 55 (5.5%) |
| Итого | 1400 | 90 (6.4%) | 3000 | 195 (6.5%) |
В каждый отдельно взятый день вариант А имел более высокий коэффициент конверсии, но в сумме побеждает вариант B. Это получилось потому, что в день с более высокой конверсией вариант B имел больший трафик. В данном примере неопытный исследователь выкатит вариант B для всего трафика, в то время как на самом деле конверсия повысится, если он использует вариант A.
На каждом сайте есть страница, которая мотивирует на покупку сильнее остальных. Предположим, мы создаем систему скоринга посетителей и выбираем для нее факторы. У нас есть страница «О продукте», и мы предполагаем, что ее посещение увеличивает вероятность конверсии. Посмотрим на данные.
| Посетил страницу | ||
| Конверсия | Нет | Да |
| Нет | 4000 | 4800 |
| Да | 400 | 320 |
| Коэффициент конверсии | 9% | 6% |
На первый взгляд все очевидно — конверсия для посетивших страницу меньше на целых 3 п.п., а значит, страница снижает вероятность конверсии. Но если мы разобьем данные на две самые важные в интернет-маркетинге когорты — десктопных и мобильных пользователей, то увидим, что на самом деле в каждой из них вероятность конверсии повышается с посещением страницы.
| Мобильный | Десктоп | |||
| Посетил страницу | Посетил страницу | |||
| Конверсия | Нет | Да | Нет | Да |
| Нет | 1600 | 4200 | 2400 | 600 |
| Да | 40 | 180 | 360 | 140 |
| Коэффициент конверсии | 2% | 4% | 13% | 19% |
Мы предполагали, что посещение страницы влияет на конверсию. На практике в дело вмешалась третья переменная — платформа пользователя. Из-за того, что она влияет не только на конверсию, но и на вероятность посещения страницы, в агрегированном состоянии она исказила данные так, что привела нас к выводам, противоположным реальному поведению пользователей.
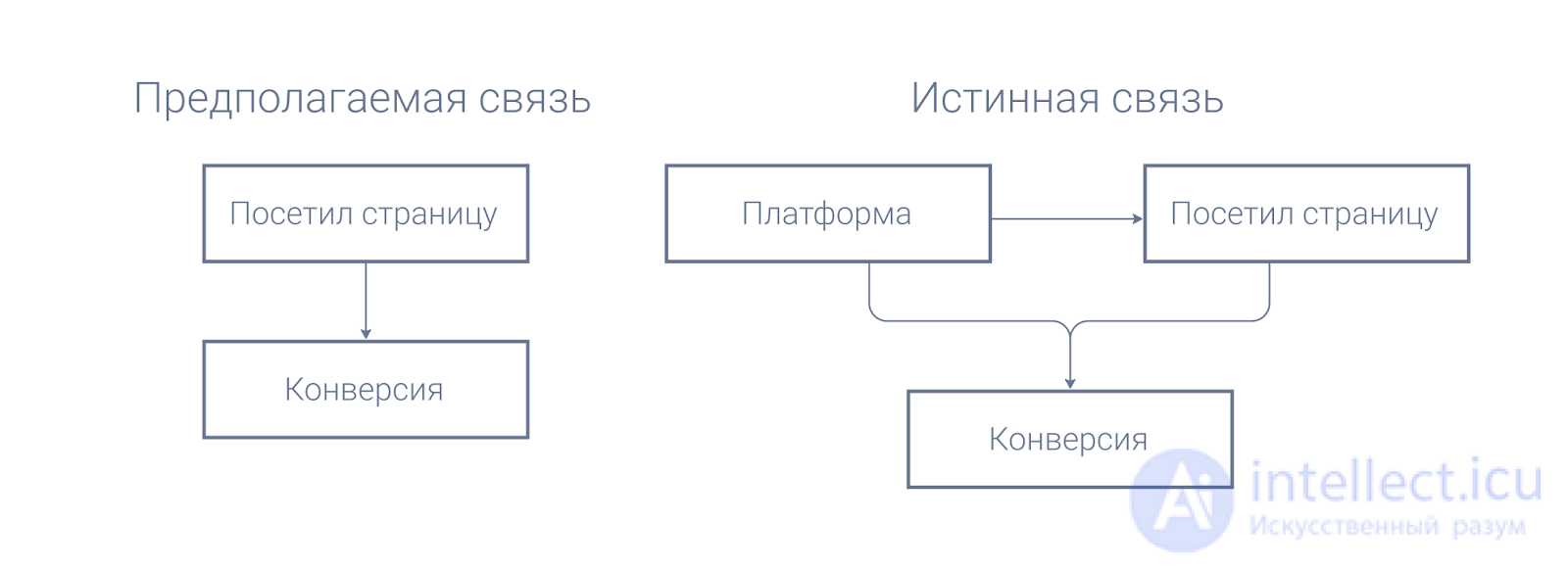
В анализе данных необходимо понимать, какая история за ними лежит: что происходит в реальном мире, как его измерили и перевели в вид данных. Поэтому исследователь данных в отделе маркетинга должен знать основы маркетинга, а в нефтегазовой отрасли — что-то о добыче полезных ископаемых. Это поможет избежать большого количества потенциальных ошибок, не последней из которых является ошибка агрегации, вызываемая парадоксом Симпсона.
К возникновению парадокса Симпсона обычно приводят следующие характеристики данных:
В каждом случае нужен индивидуальный подход. Считать, что все данные всегда необходимо разбивать на когорты — тоже неверный подход, ведь зачастую именно агрегированные данные позволяют построить самую точную модель. Кроме того, любые данные можно разбить так, чтобы получить взаимосвязь, которую нам бы хотелось получить. Правда, это не будет иметь никакого практического применения — когорты должны быть обоснованы.
Для интернет-маркетинга один из самых важных выводов — это необходимость проверять правильную работу сплиттера в A/B экспериментах. Группы пользователей в каждом тестовом варианте должны быть примерно одинаковыми. Речь не только об общем количестве пользователей, но и об их структуре. При подозрении на проблемы в первую очередь следует проверить когорты по следующим характеристикам:
Исследование, описанное в статье про Парадокс Симпсона в статистике с примерами, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Парадокс Симпсона в статистике с примерами и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ