Распределение вероятностей

Привет, сегодня поговорим про распределение вероятностей, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое распределение вероятностей , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

распределение вероятностей  — это закон, описывающий область значений случайной величины и вероятности их исхода (появления).

Определение[править ]

Определение 1. Пусть задано вероятностное пространство 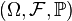, и на нем определена случайная величина 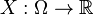. В частности, по определению, 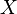является измеримым отображением измеримого пространства  в измеримое пространство , где  обозначает борелевскую сигма-алгебру на 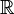. Тогда случайная величина  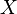индуцирует вероятностную меру  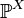на 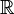 следующим образом:

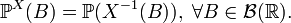
Мера 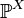 называется распределением случайной величины 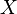. Иными словами, , таким образом  задает вероятность того, что случайная величина 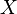 попадает во множество .

Способы задания распределений[править ]

Определение 2. Функция  называется (кумулятивной) функцией распределения случайной величины 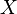. Об этом говорит сайт https://intellect.icu . Из свойств вероятности вытекает

Теорема 1. Функция распределения 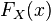 любой случайной величины удовлетворяет следующим трем свойствам:

1.  — функция неубывающая;
2. ;
3.  непрерывна справа.

Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида , вытекает

Теорема 2. Любая функция , удовлетворяющая трем свойствам, перечисленным выше, является функцией распределения для какого-то распределения .

Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.

Дискретные распределения[править ]

Определение 3. Случайная величина называется простой или дискретной, если она принимает не более, чем счетное число значений. То есть 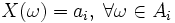, где 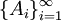 — разбиение .

Распределение простой случайной величины тогда по определению задается: 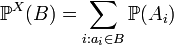. Введя обозначение 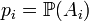, можно задать функцию . Очевидно, что 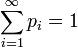. Используя счетную аддитивность , легко показать, что эта функция однозначно определяет распределение .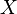

Определение 4. Функция , где 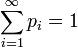 часто называется дискретным распределением.

Пример 1. Пусть функция  задана таким образом, что 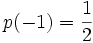 и . Эта функция задает распределение случайной величины 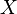, для которой  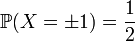(распределение Бернулли).

Теорема 3. Дискретное распределение обладает следующими свойствами:

1. ;

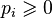2. .

Непрерывные распределения[править ]

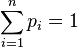Непрерывное распределение — распределение, не имеющее атомов.

Абсолютно непрерывные распределения[править ]

Абсолютно непрерывными называют распределения, имеющие плотность вероятности. Кумулятивная функция таких распределений абсолютно непрерывна в смысле Лебега.

Определение 5. Распределение случайной величины 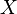 называется абсолютно непрерывным, если существует неотрицательная функция 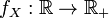, такая что . Функция  тогда называется плотностью распределения случайной величины .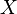

Пример 2. Пусть , когда , и 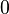 — в противном случае. Тогда , если .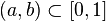

Очевидно, что для любой плотности распределения  верно равенство . Верна и обратная

Теорема 4. Если функция  такая, что:

1. ;
2. ,

то существует распределение 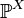 такое, что  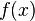является его плотностью.

Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.

Теорема 5. Если 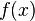 — непрерывная плотность распределения, а  — его кумулятивная функция, то

1. 
2. .

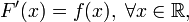
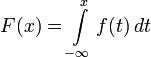Надеюсь, эта статья про распределение вероятностей, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое распределение вероятностей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ