Дисперсионный анализ

Лекция

Привет, сегодня поговорим про дисперсионный анализ, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дисперсионный анализ , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

дисперсионный анализ — метод в математической статистике, направленный на поиск зависимостей в экспериментальных данных путем исследования значимостиразличий в средних значениях. В отличие от t-критерия, позволяет сравнивать средние значения трех и более групп. Разработан Р. Фишером для анализа результатов экспериментальных исследований. В литературе также встречается обозначение ANOVA (от англ. ANalysis Of VAriance).

Типы дисперсионного анализа

Суть дисперсионного анализа сводится к изучению влияния одной или нескольких независимых переменных, обычно именуемых факторами, на зависимую переменную. Зависимые переменные представлены в виде шкал. Независимые переменные являются номинативными, то есть отражают групповую принадлежность, и могут иметь две или более градации (или уровня). Примерами независимой переменной 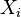Дисперсионный анализ с двумя градациями могут служить пол (женский: 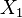, мужской: 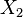) или тип экспериментальной группы (контрольная: 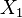, экспериментальная: 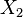). Градации, соответствующие независимым выборкам объектов, называются межгрупповыми, а градации, соответствующие зависимым выборкам, — внутригрупповыми.

В зависимости от типа и количества переменных, различают

Математическая модель дисперсионного анализа

Математическая модель дисперсионного анализа представляет собой частный случай основной линейной модели. Пусть с помощью методов Дисперсионный анализ производится измерение нескольких параметров 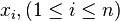, чьи точные значения — 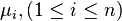. В таком случае, результаты измерений различных величин различными методами можно представить как:

$x_{i,j} = \mu_{i} + a_{i,j} + e_{i,j}$ ,

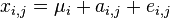где:

Тогда дисперсии следующих случайных величин:
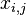
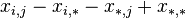
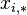
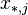
Дисперсионный анализ

(где:

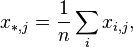
$x_{*,j} = \frac{1}{n} \sum_{i} x_{i,j},$

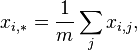
$x_{i,*} = \frac{1}{m} \sum_{j} x_{i,j},$

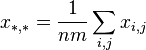
$x_{*,*} = \frac{1}{nm} \sum_{i, j} x_{i,j}$

) выражаются как:

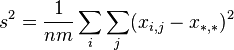
$s^{2} = \frac{1}{nm} \sum_{i} \sum_{j} ( x_{i,j} - x_{*,*} )^{2}$

$s_{0}^2 = \frac{1}{nm} \sum_{i} \sum_{j} ( x_{i,j} - x_{i,*} - x_{*,j} + x_{*,*} )^{2}$

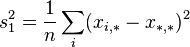
$s_{1}^2 = \frac{1}{n} \sum_{i} ( x_{i,*} - x_{*,*} )^{2}$

$s_{2}^2 = \frac{1}{m} \sum_{j} ( x_{*,j} - x_{*,*} )^{2}$

и удовлетворяют тождеству:

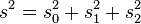
$s^2 = s_{0}^2 + s_{1}^2 + s_{2}^2$

Процедура дисперсионного анализа состоит в определении соотношения систематической (межгрупповой) дисперсии к случайной (внутригрупповой) дисперсии в измеряемых данных. В качестве показателя изменчивости используется сумма квадратов отклонения значений параметра от среднего: 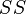Дисперсионный анализ (от англ. Sum of Squares). 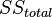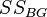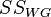Можно показать, что общая сумма квадратов раскладывается на межгрупповую сумму квадратов и внутригрупповую сумму квадратов Дисперсионный анализ :

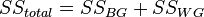
$SS_{total} = SS_{BG} + SS_{WG}$

Пусть точное значение каждого параметра есть его математическое ожидание, равное среднему генеральной совокупности 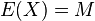Дисперсионный анализ . При отсутствии систематических ошибок групповое среднее и среднее генеральной совокупности тождественны: 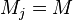. Тогда случайная ошибка измерения есть разница между результатом измерения 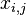Дисперсионный анализ и средним группы: 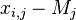. Если же метод 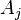оказывает систематическое воздействие, то систематическая ошибка при воздействии этого фактора есть разница между средним группы Дисперсионный анализ и средним генеральной совокупности: 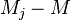. Тогда уравнение 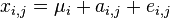может быть представлено в следующем виде:

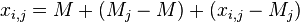Дисперсионный анализ , или

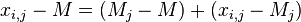Дисперсионный анализ .

Тогда

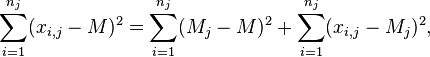
$\begin{align} \sum_{i = 1}^{n_j} (x_{i,j} - M)^2 &= \sum_{i = 1}^{n_j} (M_j - M)^2 + \sum_{i = 1}^{n_j} (x_{i,j} - M_j)^2 ,\\ \end{align}$

где

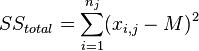
$SS_{total} = \sum_{i = 1}^{n_j} (x_{i,j} - M)^2$

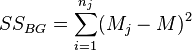
$SS_{BG} = \sum_{i = 1}^{n_j} (M_j - M)^2$

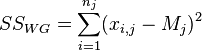
$SS_{WG} = \sum_{i = 1}^{n_j} (x_{i,j} - M_j)^2$

Следовательно

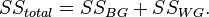
$SS_{total} = SS_{BG} + SS_{WG}.$

Аналогичным образом раскладываются степени свободы:

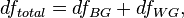$df_{total} = df_{BG} + df_{WG},$ где

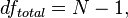
$df_{total} = N - 1,$

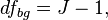
$df_{bg} = J - 1,$

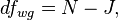
$df_{wg} = N - J,$

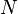и Дисперсионный анализ есть объем полной выборки, а 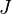— количество групп.

Тогда дисперсия каждой части, именуемая в модели дисперсионного анализа как «средний квадрат», или 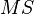Дисперсионный анализ (от англ. Mean Square), есть отношение суммы квадратов к числу их степеней свободы:

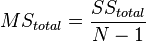
$MS_{total} = \frac {SS_{total}}{N - 1}$

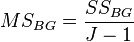
$MS_{BG} = \frac {SS_{BG}}{J - 1}$

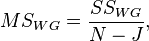
$MS_{WG} = \frac {SS_{WG}}{N - J},$

Соотношение межгрупповой и внутригрупповой дисперсий имеет F-распределение (распределение Фишера) и определяется при помощи (F-критерия Фишера):

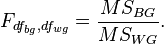
Дисперсионный анализ

Принципы и применение

Исходными положениями дисперсионного анализа являются

Нулевой гипотезой в дисперсионном анализе является утверждение о равенстве средних значений:

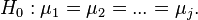
$H_0: \mu_1 = \mu_2 = ... = \mu_j.$

При отклонении нулевой гипотезы принимается альтернативная гипотеза о том, что не все средние равны, то есть имеются по крайней мере две группы, отличающиеся средними значениями:

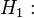
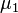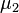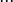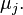
Дисперсионный анализ ≠ ≠ ≠

При наличии трех и более групп для определения различий между средними применяются post-hoc t-тесты или метод контрастов.

Однофакторный дисперсионный анализ

Простейшим случаем дисперсионного анализа является одномерный однофакторный анализ для двух или нескольких независимых групп, когда все группы объединены по одному признаку. В ходе анализа проверяется нулевая гипотеза о равенстве средних. При анализе двух групп дисперсионный анализ тождественен двухвыборочному t-критерию Стьюдента для независимых выборок, и величина F-статистики равна квадрату соответствующей t-статистики.

Для подтверждения положения о равенстве дисперсий обычно применяется критерий Ливена (Levene's test). В случае отвержения гипотезы о равенстве дисперсий основной анализ неприменим. Если дисперсии равны, то для оценки соотношения межгрупповой и внутригрупповой изменчивости применяется F-критерий Фишера:

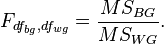
Дисперсионный анализ

Если F-статистка превышает критическое значение, то нулевая гипотеза отвергается и делается вывод о неравенстве средних. При анализе средних двух групп результаты могут быть быть интерпретированы непосредственно после применения критерия Фишера.

При наличии трех и более групп требуется попарное сравнение средних для выявления статистически значимых отличий между ними. Априорный анализ включает метод контрастов, при котором межгрупповая сумма квадратов дробится на суммы квадратов отдельных контрастов:

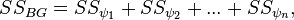
$SS_{BG} = SS_{\psi_1} + SS_{\psi_2} + ... + SS_{\psi_n},$

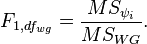
где Дисперсионный анализ есть контраст между средними двух групп, и затем при помощи критерия Фишера проверяется соотношение среднего квадрата для каждого контраста к внутригрупповому среднему квадрату:

Дисперсионный анализ

Апостериорный анализ включает post-hoc t-критерии по методам Бонферрони или Шеффе, а также сравнение разностей средних по методу Тьюки. Особенностью post-hoc тестов является использование внутригруппового среднего квадрата Дисперсионный анализ для оценки любых пар средних. 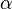Тесты по методам Бонферрони и Шеффе являются наиболее консервативными, так как они используют наименьшую критическую область при заданном уровне значимости Дисперсионный анализ .

Помимо оценки средних, дисперсионный анализ включает определение коэффициента детерминации 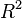, показывающего, какую долю общей изменчивости объясняет данный фактор:

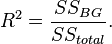
Дисперсионный анализ

Многофакторный дисперсионный анализ

Многофакторный анализ позволяет проверить влияние нескольких факторов на зависимую переменную. Линейная модель многофакторной модели имеет вид

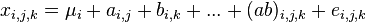$x_{i,j,k} = \mu_{i} + a_{i,j} + b_{i,k} + ... + (ab)_{i,j,k} + e_{i,j,k}$ ,

где:

В отличие от однофакторной модели, где имеется одна межгрупповая сумма квадратов, модель многофакторного анализа включает суммы квадратов для каждого фактора в отдельности и суммы квадратов всех взаимодействий между ними. Так, в двухфакторной модели межгрупповая сумма квадратов раскладывается на сумму квадратов фактора 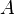Дисперсионный анализ , сумму квадратов фактора 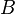и сумму квадратов взаимодействия факторов 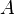и :

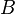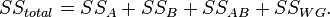
$SS_{total} = SS_{A} + SS_{B} + SS_{AB} + SS_{WG}.$

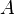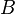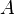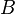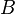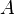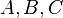Соответственно, трехфакторная модель включает сумму квадратов фактора Дисперсионный анализ , сумму квадратов фактора , сумму квадратов фактора и суммы квадратов взаимодействий факторов и , и , и , а также взаимодействия всех трех факторов Дисперсионный анализ :

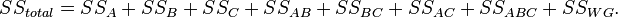
$SS_{total} = SS_{A} + SS_{B} + SS_{C} + SS_{AB} + SS_{BC} + SS_{AC} + SS_{ABC} + SS_{WG}.$

Степени свободы раскладываются аналогичным образом:

$df_{total} = df_A + df_B + df_{AB} + df_{WG},$ где

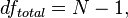
$df_{total} = N - 1,$

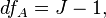
$df_A = J - 1,$

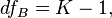
$df_B = K - 1,$

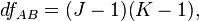
$df_{AB} = (J - 1)(K - 1),$

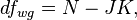
$df_{wg} = N - JK,$

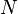и Дисперсионный анализ есть объем полной выборки, 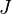— количество уровней (групп) фактор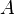а , а 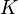— количество уровней (групп) фактора .

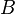В ходе анализа проверяются несколько нулевых гипотез:

Каждая гипотеза проверяется с помощью критерия Фишера:

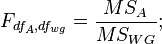
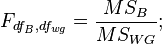
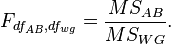
Дисперсионный анализ

При отвержении нулевой гипотезы о влиянии отдельного фактора принимается утверждение, что присутствует главный эффект фактора 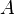Дисперсионный анализ ( и т. д.). При отвержении нулевой гипотезы о взаимодействии факторов принимается утверждение о том, что влияние фактора 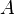проявляется по-разному на разных уровнях фактора 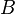Дисперсионный анализ . Обычно в таком случае результаты общего анализа признаются не имеющими силы, и влияние фактора 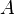проверяется отдельно на каждом уровне фактора 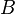Дисперсионный анализ с помощью однофакторного дисперсионного анализа или t-критерия.

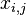однофакторный и многофакторный дисперсионный анализ (одна или несколько независимых переменных);
одномерный и многомерный дисперсионный анализ (одна или несколько зависимых переменных);
дисперсионный анализ с повторными измерениями (для зависимых выборок);
дисперсионный анализ с постоянными факторами, случайными факторами, и смешанные модели с факторами обоих типов;
— результат измерения 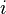-го параметра по методу ;
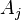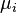— точное значение 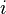-го параметра;
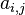— систематическая ошибка измерения 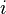-го параметра в группе по методу ;
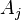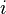— случайная ошибка измерения -го параметра по методу .
нормальное распределение зависимой переменной;
равенство дисперсий в сравниваемых генеральных совокупностях;
случайный и независимый характер выборки.
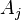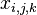— результат измерения 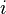-го параметра;
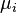— среднее для 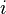-го параметра;
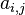— систематическая ошибка измерения 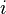-го параметра в 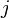группе по методу ;
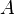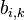— систематическая ошибка измерения 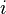-го параметра в 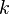группе по методу ;
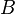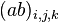— систематическая ошибка измерения 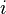-го параметра в 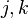группе в силу комбинации методов 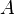и ;
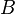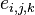— случайная ошибка измерения 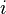-го параметра.
гипотеза о равенстве средних под влиянием фактора : ;
гипотеза о равенстве средних под влиянием фактора : ;
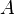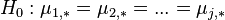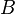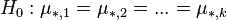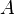гипотеза об отсутствии взаимодействия факторов и 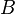: для всех 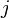и
Основные идеи
- Разбиение суммы квадратов
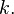
- Многофакторный дисперсионный анализ
- Эффекты взаимодействия
Сложные планы
- Межгрупповые планы и планы повторных измерений
- Неполные (гнездовые) планы
Ковариационный анализ (ANCOVA)
- Фиксированные ковариаты
- Переменные ковариаты
Многомерные планы: многомерный дисперсионный и ковариационный анализ
- Межгрупповые планы
- Планы с повторными измерениями
- Суммы значений переменной и дисперсионного анализа
Анализ контрастов и апостериорные критерии
- Почему сравниваютсяотдельные множества средних?
- Анализ контрастов
- Апостериорные критерии
Предположения и эффекты их нарушения
- Нормальность распределения
- Однородность дисперсии
- Однородность дисперсии и ковариации
- Сферичность и сложная симметрия
Методы дисперсионного анализа

Этот раздел содержит вводный обзор и обсуждение некоторых методов дисперсионного анализа, включая планы с повторными измерениями, ковариационный анализ, многомерный дисперсионный анализ, несбалансированные и вложенные планы, эффекты контрастов, апостериорные сравнения и др. Дополнительно, можно обратиться к разделу Компоненты дисперсии(разделы связанные с оцениванием компонент дисперсии в смешанных планах), Планирование эксперимента (разделы связанные со специальными областями применения дисперсионного анализа в промышленных условиях), а также Анализ повторяемости и воспроизводимости (разделы, относящиеся к оцениванию надежности и точности измерительных систем).

Основные идеи

Цель дисперсионного анализа.

Основной целью дисперсионного анализа является исследование значимости различия между средними. Раздел Элементарные понятия статистики содержит краткое введение в исследование статистической значимости. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений). Если вы не достаточно знакомы с этими критериями, рекомендуем обратиться к разделу Основные статистики и таблицы.

Откуда произошло название Дисперсионный анализ?Может показаться странным, что процедура сравнения средних называется дисперсионным анализом. В действительности, это связано с тем, что при исследовании статистической значимости различия между средними двух (или нескольких) групп, мы на самом деле сравниваем (т.е. анализируем) выборочные дисперсии. Фундаментальная концепция дисперсионного анализа предложена Фишером в 1920 году. Возможно, более естественным был бы термин анализ суммы квадратов или анализ вариации, но в силу традиции употребляется термин дисперсионный анализ.

Разбиение суммы квадратов
Многофакторный дисперсионный анализ
Эффекты взаимодействия

Также смотрите разделы.

Сложные планы
Ковариационный анализ (ANCOVA)
Многомерные планы: многомерный дисперсионный и ковариационный анализ
Анализ контрастов и апостериорные критерии
Предположения и эффекты их нарушения

См. Методы дисперсионного анализа, Компоненты дисперсии и смешанная модель ANOVA/ANCOVA, а также Планироване эксперимента.

Разбиение суммы квадратов

Для выборки объема n выборочная дисперсия вычисляется как сумма квадратов отклонений от выборочного среднего, деленная на n-1 (объем выборки минус единица). Таким образом, при фиксированном объеме выборки n дисперсия есть функция суммы квадратов (отклонений), обозначаемая, для краткости, SS (от английского Sum of Squares - Сумма квадратов). Далее слово выборочная мы часто опускаем, прекрасно понимая, что рассматривается выборочная дисперсия или оценка дисперсии. В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Рассмотрим следующий набор данных:

	Группа 1	Группа 2
Наблюдение 1 Наблюдение 2 Наблюдение 3	2 3 1	6 7 5
Среднее Сумма квадратов (СК)	2 2	6 2
Общее среднее Общая сумма квадратов	4 28

Средние двух групп существенно различны (2 и 6 соответственно). Сумма квадратов отклонений внутри каждой группы равна 2. Складывая их, получаем 4. Если теперь повторить эти вычисления без учета групповой принадлежности, то есть, если вычислить SS исходя из общего среднего этих двух выборок, то получим величину 28. Иными словами, дисперсия (сумма квадратов), основанная на внутригрупповой изменчивости, приводит к гораздо меньшим значениям, чем при вычислении на основе общей изменчивости (относительно общего среднего). Причина этого, очевидно, заключается в существенной разнице между средними значениями, и это различие между средними и объясняет существующее различие между суммами квадратов. В самом деле, если использовать для анализа этих данных модуль Дисперсионный анализ, то будет получена следующая таблица, называемая таблицей дисперсионного анализа:

	ГЛАВНЫЙ ЭФФЕКТ
	SS	ст.св.	MS	F	p
Эффект Ошибка	24.0 4.0	1 4	24.0 1.0	24.0	.008

Как видно из таблицы, общая сумма квадратов SS = 28 разбита на компоненты: сумму квадратов, обусловленную внутригрупповой изменчивостью (2+2=4; см. вторую строку таблицы) и сумму квадратов, обусловленную различием средних значений между группами (28-(2+2)=24; см первую строку таблицы). Заметим, что MS в этой таблице есть средний квадрат, равный SS, деленная на число степеней свободы (ст.св).

SS ошибок и SS эффекта. Внутригрупповая изменчивость (SS) обычно называется остаточной компонентой или дисперсией ошибки. Это означает, что обычно при проведении эксперимента она не может быть предсказана или объяснена. С другой стороны, SS эффекта (или компоненту дисперсии между группами) можно объяснить различием между средними значениями в группах. Иными словами, принадлежность к некоторой группе объясняет межгрупповую изменчивость, т.к. нам известно, что эти группы обладают разными средними значениями.

Проверка значимости.Основные идеи проверки статистической значимости обсуждаются в разделе Элементарные понятия статистики. В этом же разделе объясняются причины, по которым многие критерии используют отношение объясненной и необъясненной дисперсии. Примером такого использования является сам дисперсионный анализ. Проверка значимости в дисперсионном анализе основана на сравнении компоненты дисперсии, обусловленной межгрупповым разбросом (называемой средним квадратом эффекта или MSэффект) и компоненты дисперсии, обусловленной внутригрупповым разбросом (называемой средним квадратом ошибки или MSошибка; эти термины были впервые использованы в работе Edgeworth, 1885). Если верна нулевая гипотеза (равенство средних в двух популяциях), то можно ожидать сравнительно небольшое различие выборочных средних из-за чисто случайной изменчивости. Поэтому, при нулевой гипотезе, внутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета групповой принадлежности. Полученные внутригрупповые дисперсии можно сравнить с помощью F-критерия, проверяющего, действительно ли отношение дисперсий значимо больше 1. В рассмотренном выше примере F-критерий показывает, что различие между средними статистически значимо (значимо на уровне 0.008).

Основная логика дисперсионного анализа. Подводя итоги, можно сказать, что целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.

Зависимые и независимые переменные. Переменные, значения которых определяется с помощью измерений в ходе эксперимента (например, балл, набранный при тестировании), называютсязависимыми переменными. Переменные, которыми можно управлять при проведении эксперимента (например, методы обучения или другие критерии, позволяющие разделить наблюдения на группы или классифицировать) называются факторами или независимыми переменными. Более подробно эти понятия описаны в разделе Элементарные понятия статистики.

Многофакторный дисперсионный анализ

В рассмотренном выше простом примере вы могли бы сразу вычислить t-критерий для независимых выборок, используя соответствующую опцию модуля Основные статистики и таблицы.Полученные результаты, естественно, совпадут с результатами дисперсионного анализа. Однако дисперсионный анализ содержит гораздо более гибкие и мощные технические средства, позволяющие исследовать планы практически неограниченной сложности.

Множество факторов. Мир по своей природе сложен и многомерен. Ситуации, когда некоторое явление полностью описывается одной переменной, чрезвычайно редки. Например, если мы пытаемся научиться выращивать большие помидоры, следует рассматривать факторы, связанные с генетической структурой растений, типом почвы, освещенностью, температурой и т.д. Таким образом, при проведении типичного эксперимента приходится иметь дело с большим количеством факторов. Основная причина, по которой использование дисперсионного анализа предпочтительнее повторного сравнения двух выборок при разных уровнях факторов с помощью серий t-критерия, заключается в том, что дисперсионный анализ существенно болееэффективен и, для малых выборок, более информативен.

продолжение следует...

Продолжение:

Часть 1 Дисперсионный анализ
Часть 2 - Дисперсионный анализ
Часть 3 Вау!! 😲 Ты еще не читал? Это зря! - Дисперсионный анализ

См.также

Методы дисперсионного анализа,
Компоненты дисперсии и смешанные модели
ANOVA/ANCOVA
Планирование эксперимента.
Элементарные понятия статистики
Основные статистики и таблицы

В начало

Надеюсь, эта статья про дисперсионный анализ, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое дисперсионный анализ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Дисперсионный анализ

Типы дисперсионного анализа

Математическая модель дисперсионного анализа

Принципы и применение

Однофакторный дисперсионный анализ

Многофакторный дисперсионный анализ

Продолжение:

См.также

Комментарии

Оставить комментарий

Теория вероятностей. Математическая статистика и Стохастический анализ

Термины: Теория вероятностей. Математическая статистика и Стохастический анализ