17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации кратко

Привет, Вы узнаете о том , что такое определение характеристик эргодической стационарной случайной функции по одной реализации, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое определение характеристик эргодической стационарной случайной функции по одной реализации , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Рассмотрим стационарную случайную функцию , обладающую эргодическим свойством, и предположим, что в нашем распоряжении имеется всего одна реализация этой случайной функции, но зато на достаточно большом участке времени 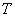. Для эргодической стационарной случайной функции одна реализация достаточно большой продолжительности практически эквивалентна (в смысле объема сведений о случайной функции) множеству реализаций той же общей продолжительности; характеристики случайной функции могут быть приближенно определены не как средние по множеству наблюдений, а как средние по времени 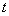. В частности, при достаточно большом  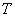математическое ожидание  может быть приближенно вычислено по формуле

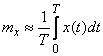.                     (17.8.1)

Аналогично может быть приближенно найдена корреляционная функция 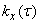 при любом . Действительно, корреляционная функция, по определению, представляет собой не что иное, как математическое ожидание случайной функции :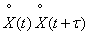

                   (17.8.2)

Это математическое ожидание также, очевидно, может быть приближенно вычислено как среднее по времени.

Фиксируем некоторое значение  и вычислим указанным способом корреляционную функцию 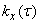. Для этого удобно предварительно «центрировать» данную реализацию , т. е. вычесть из нее математическое ожидание (17.8.1):

.                            (17.8.3)

Вычислим при заданном  математическое ожидание случайной функции 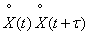 как среднее по времени. При этом, очевидно, нам придется учитывать не весь участок времени от 0 до 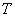, а несколько меньший, так как второй сомножитель  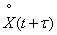известен нам не для всех 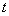, а только для тех, для которых .

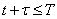Вычисляя среднее по времени указанным выше способом, получим:

.                   (17.8.4)

Вычислив интеграл (17.8.4) для ряда значений , можно приближенно воспроизвести по точкам весь ход корреляционной функции.

На практике обычно интегралы (17.8.1) и (17.8.4) заменяют конечными суммами. Покажем, как это делается. Разобьем интервал записи случайной функции на 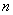 равных частей длиной  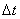и обозначим середины полученных участков  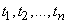(рис. 17.8.1).

Рис. 17.8.1.

Предоставим интеграл (17.8.1) как сумму интегралов по элементарным участкам 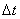 и на каждом из них вынесем функцию  из-под знака интеграла средним значением, соответствующим центру интервала . Получим приближенно:

,

или

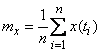.             (17.8.5)

Аналогично можно вычислить корреляционную функцию для значений , равных 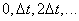. Придадим, например, величине  значение

вычислим интеграл (17.8.4), деля интервал интегрирования

на  равных участков длиной 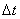 и вынося на каждом из них функцию  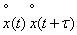за знак интеграла средним значением. Получим:

,

или окончательно

.               (17.8.6)

Вычисление корреляционной функции по формуле (17.8.6) производят для 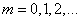 последовательно вплоть до таких значений 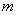, при которых корреляционная функция становится практически равной нулю или начинает совершать небольшие нерегулярные колебания около нуля. Общий ход функции  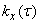воспроизводится по отдельным точкам (рис. 17.8.2).

Рис. 17.8.2.

Для того чтобы математическое ожидание  и корреляционная функция 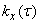 были определены с удовлетворительной точностью, нужно, чтобы число точек  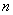было достаточно велико (порядка сотни, а в некоторых случаях даже нескольких сотен). Выбор длины элементарного участка  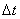определяется характером изменения случайной функции. Если случайная функция изменяется сравнительно плавно, участок  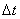можно выбирать большим, чем когда она совершает резкие и частые колебания. Чем более высокочастотный состав имеют колебания, образующие случайную функцию, тем чаще нужно располагать опорные точки при обработке. Ориентировочно можно рекомендовать выбирать элементарный участок  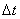так, чтобы на полный период самой высокочастотной гармоники в составе случайной функции приходилось порядка 5-10 опорных точек.

Часто выбор опорных точек вообще не зависит от обрабатывающего, а диктуется темпом работы записывающей аппаратуры. В этом случае следует вести обработку непосредственно полученного из опыта материала, не пытаясь вставить между наблюденными значениями промежуточные, так как эхо не может повысить точности результата, а излишне осложнит обработку.

Пример. В условиях горизонтального полета самолета произведена запись вертикальной перегрузки, действующей на самолет. Перегрузка регистрировалась на участке времени 200 сек с интервалом 2 сек. Результаты приведены в таблице 17.8.1.

Таблица 17.8.1

Считая процесс изменения перегрузки стационарным, определить приближенно математическое ожидание перегрузки 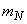, дисперсию  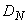и нормированную корреляционную функцию 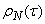. Об этом говорит сайт https://intellect.icu . Аппроксимировать  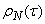какой-либо аналитической функцией, найти и построить спектральную плотность случайного процесса.

Решение. По формуле (17.8.5) имеем:

.

Центрируем случайную функцию (табл. 17.8.2).

Таблица 17.8.2

Возводя в квадрат все значения  и деля сумму на  получим приближенно дисперсию случайной функции :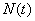

и среднее квадратическое отклонение:

.

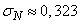Перемножая значения , разделенные интервалом 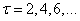, и деля сумму произведений соответственно на ; ; ; …, получим значения корреляционной функции 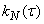. Нормируя корреляционную функцию делением на 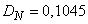, получим таблицу значений функции  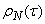(табл. 17.8.3).

Таблица 17.8.3

График функции 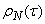 представлен на рис. 17.8.3 в виде точек, соединенных пунктиром.

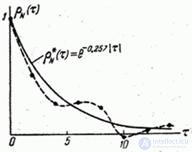
Рис. 17.8.3.

Не вполне гладкий ход корреляционной функции может быть объяснен недостаточным объемом экспериментальных данных (недостаточной продолжительностью опыта), в связи с чем случайные неровности в ходе функции не успевают сгладиться. Вычисление 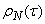 продолжено до таких значений при которых фактически корреляционная связь пропадает.

Для того чтобы сгладить явно незакономерные колебания экспериментально найденной функции 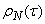, заменим ее приближенно функцией вида:

,

где параметр  подберем методом наименьших квадратов (см.  14.5).

Применяя этот метод, находим . Вычисляя значения функции  при , построим график сглаживающей кривой. На рис. 17.8.3 он проведен сплошной линией. В последнем столбце таблицы 17.8.3 приведены значения функции .

Пользуясь приближенным выражением корреляционной функции (17.8.6), получим (см.  17.4, пример 1) нормированную спектральную плотность случайного процесса в виде:

.

График нормированной спектральной плотности представлен на рис. 17.8.4.

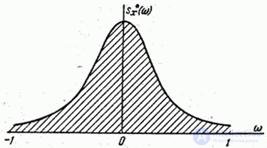
Рис. 17.8.4.

Информация, изложенная в данной статье про определение характеристик эргодической стационарной случайной функции по одной реализации , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое определение характеристик эргодической стационарной случайной функции по одной реализации и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ