Лекция
Привет, Вы узнаете о том , что такое моменты случайной величины, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое моменты случайной величины, дисперсия, среднее квадратичное отклонение, коэффициент асимметрии, коэффициент вариации, , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Кроме характеристик положения – средних, типичных значений случайной величины, - употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик чаще всего применяются так называемые моменты.
Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Совершенно теми же приемами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.
Начальным моментом s-го порядка прерывной случайной величины 
называется сумма вида:
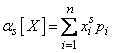. (5.7.1)
Очевидно, это определение совпадает с определением начального момента порядка s в механике, если на оси абсцисс в точках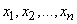 
сосредоточены массы 
.
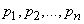Для непрерывной случайной величины Х начальным моментом s-го порядка называется интеграл
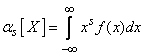. (5.7.2)
Нетрудно убедиться, что введенная в предыдущем n° основная характеристика положения – математическое ожидание – представляет собой не что иное, как первый начальный момент случайной величины .
Пользуясь знаком математического ожидания, можно объединить две формулы (5.7.1) и (5.7.2) в одну. Действительно, формулы (5.7.1) и (5.7.2) по структуре полностью аналогичны формулам (5.6.1) и (5.6.2), с той разницей, что в них вместо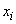 
и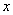 
стоят, соответственно, 
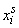и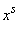 
. Поэтому можно написать общее определение начального момента 
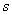-го порядка, справедливое как для прерывных, так и для непрерывных величин:
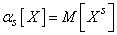, (5.7.3)
т.е. начальным моментом 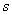-го порядка случайной величины называется математическое ожидание 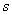-й степени этой случайной величины.
Перед тем, как дать определение центрального момента, введем новое понятие «центрированной случайной величины».
Пусть имеется случайная величина с математическим ожиданием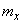 
. Центрированной случайной величиной, соответствующей величине , называется отклонение случайной величины от ее математического ожидания:
. (5.7.4)
Условимся в дальнейшем везде обозначать центрированную случайную величину, соответствующую данной случайной величине, той же буквой со значком 
наверху.
Нетрудно убедиться, что математическое ожидание центрированной случайной величины равно нулю. Действительно, для прерывной величины
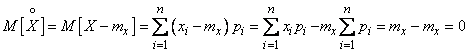; (5.7.5)
аналогично и для непрерывной величины.
Центрирование случайной величины, очевидно, равносильно переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию.
Моменты центрированной случайной величины носят название центральных моментов. Они аналогичны моментам относительно центра тяжести в механике.
Таким образом, центральным моментом порядка s случайной величины называется математическое ожидание 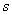-й степени соответствующей центрированной случайной величины:
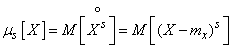, (5.7.6)
а для непрерывной – интегралом
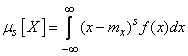. (5.7.8)
В дальнейшем в тех случаях, когда не возникает сомнений, к какой случайной величине относится данный момент, мы будем для краткости вместо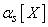 
и 
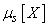писать просто 
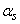и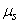 
.
Очевидно, для любой случайной величины центральный момент первого порядка равен нулю:
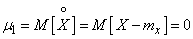, (5.7.9)
так как математическое ожидание центрированной случайной величины всегда равно нулю.
Выведем соотношения, связывающие центральные и начальные моменты различных порядков. Вывод мы проведем только для прерывных величин; легко убедится, что точно те же соотношения справедливы и для непрерывных величин, если заменить конечные суммы интегралами, а вероятности – элементами вероятности.
Рассмотрим второй центральный момент:
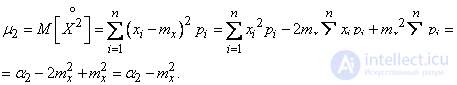
Аналогично для третьего центрального момента получим:
Выражения для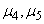 
и т.д. могут быть получены аналогичным путем.
Таким образом, для центральных моментов любой случайной величины справедливы формулы:
(5.7.10)
Вообще говоря, моменты могут рассматриваться не только относительно начала координат (начальные моменты) или математического ожидания (центральные моменты), но и относительно произвольной точки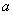 
:
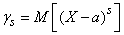. (5.7.11)
Однако центральные моменты имеют перед всеми другими преимущество: первый центральный момент, как мы видели, всегда равен нулю, а следующий за ним, второй центральный момент при этой системе отсчета имеет минимальное значение. Докажем это. Для прерывной случайной величины при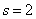 
формула (5.7.11) имеет вид:
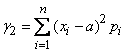. (5.7.12)
Преобразуем это выражение:
Очевидно, эта величина достигает своего минимума, когда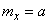 
, т.е. когда момент берется относительно точки .
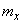Из всех моментов в качестве характеристик случайной величины чаще всего применяются первый начальный момент (математическое ожидание)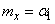 
и второй центральный момент 
.
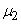Второй центральный момент называется дисперсией случайной величины. Ввиду крайней важности этой характеристики среди других моментов введем для нее специальное обозначение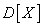 
:
.
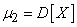Согласно определению центрального момента
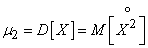, (5.7.13)
т.е. дисперсией случайной величины Х называется математическое ожидание квадрата соответствующей центрированной величины.
Заменяя в выражении (5.7.13) величину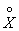 
ее выражением, имеем также:
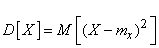. Об этом говорит сайт https://intellect.icu . (5.7.14)
Для непосредственного вычисления дисперсии служат формулы:
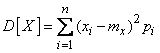, (5.7.15)
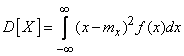(5.7.16)
- соответственно для прерывных и непрерывных величин.
дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около ее математического ожидания. Само слово «дисперсия» означает «рассеивание».
Если обратиться к механической интерпретации распределения, то дисперсия представляет собой не что иное, как момент инерции заданного распределения масс относительно центра тяжести (математического ожидания).
Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (иначе – «стандартом») случайной величины . Среднее квадратическое отклонение будем обозначать 
:
, (5.7.17)
Для упрощения записей мы часто будем пользоваться сокращенными обозначениями среднего квадратического отклонения и дисперси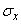и: 
и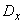 
. В случае, когда не возникает сомнения, к какой случайной величине относятся эти характеристики, мы будем иногда опускать значок х у 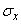и и 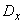писать просто 
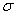и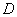 
. Слова «среднее квадратическое отклонение» иногда будем сокращенно заменять буквами с.к.о.
На практике часто применяется формула, выражающая дисперсию случайной величины через ее второй начальный момент (вторая из формул (5.7.10)). В новых обозначениях она будет иметь вид:
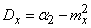. (5.7.18)
Математическое ожидание 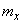и дисперсия 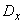(или среднее квардратическое отклонение 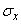) – наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения применяются моменты высших порядков.
Третий центральный момент служит для характеристики асимметрии (или «скошенности») распределения. Если распределение симметрично относительно математического ожидания (или, в механической интерпретации, масса распределена симметрично относительно центра тяжести), то все моменты нечетного порядка (если они существуют) равны нулю. Действительно, в сумме
при симметричном относительно 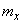законе распределения и нечетном 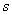каждому положительному слагаемому соответствует равное ему по абсолютной величине отрицательное слагаемое, так что вся сумма равна нулю. То же, очевидно, справедливо и для интеграла
,
который равен нулю, как интеграл в симметричных пределах от нечетной функции.
Естественно поэтому в качестве характеристики асимметрии распределения выбрать какой-либо из нечетных моментов. Простейший из них есть третий центральный момент. Он имеет размерность куба случайной величины: чтобы получить безразмерную характеристику, третий момент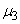 
делят на куб среднего квадратического отклонения. Полученная величина носит название «
коэффициент асимметрии » или просто «асимметрии»; мы обозначим ее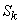 
:
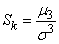. (5.7.19)
На рис. 5.7.1 показано два асимметричных распределения; одно из них (кривая I) имеет положительную асимметрию (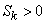
); другое (кривая II) – отрицательную (
).
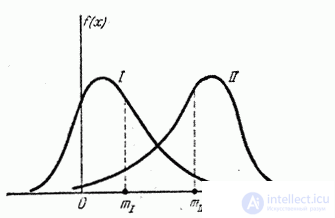
Рис. 5.7.1
Четвертый центральный момент служит для характеристики так называемой «крутости», т.е. островершинности или плосковершинности распределения. Эти свойства распределения описываются с помощью так называемого эксцесса. Эксцессом случайной величины называется величина
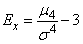. (5.7.20)
Число 3 вычитается из отношения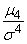 
потому, что для весьма важного и широко распространенного в природе нормального закона распределения (с которым мы подробно познакомимся в дальнейшем) 
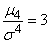. Таки образом, для нормального распределения эксцесс равен нулю; кривые, более островершинные по сравнении с нормальной, обладают положительным эксцессом; кривые более плосковершинные – отрицательным эксцессом.
На рис. 5.7.2 представлены: нормальное распределение (кривая I), распределение с положительным эксцессом (кривая II) и распределение с отрицательным эксцессом (кривая III).
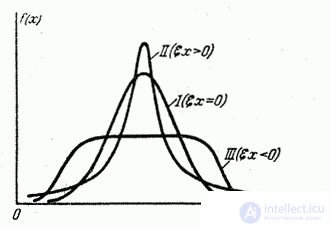
Рис. 5.7.2
Кроме рассмотренных выше начальных и центральных моментов, на практике иногда применяются так называемые абсолютные моменты (начальные и центральные), определяемые формулами
; 
.
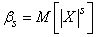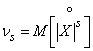Очевидно, абсолютные моменты четных порядков совпадают с обычными моментами.
Из абсолютных моментов наиболее часто применяется первый абсолютный центральный момент
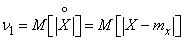, (5.7.21)
называемый средним арифметическим отклонением (САО). Наряду с дисперсией и средним квадратическим отклонением среднее арифметическое отклонение иногда применяется как характеристика рассеивания.
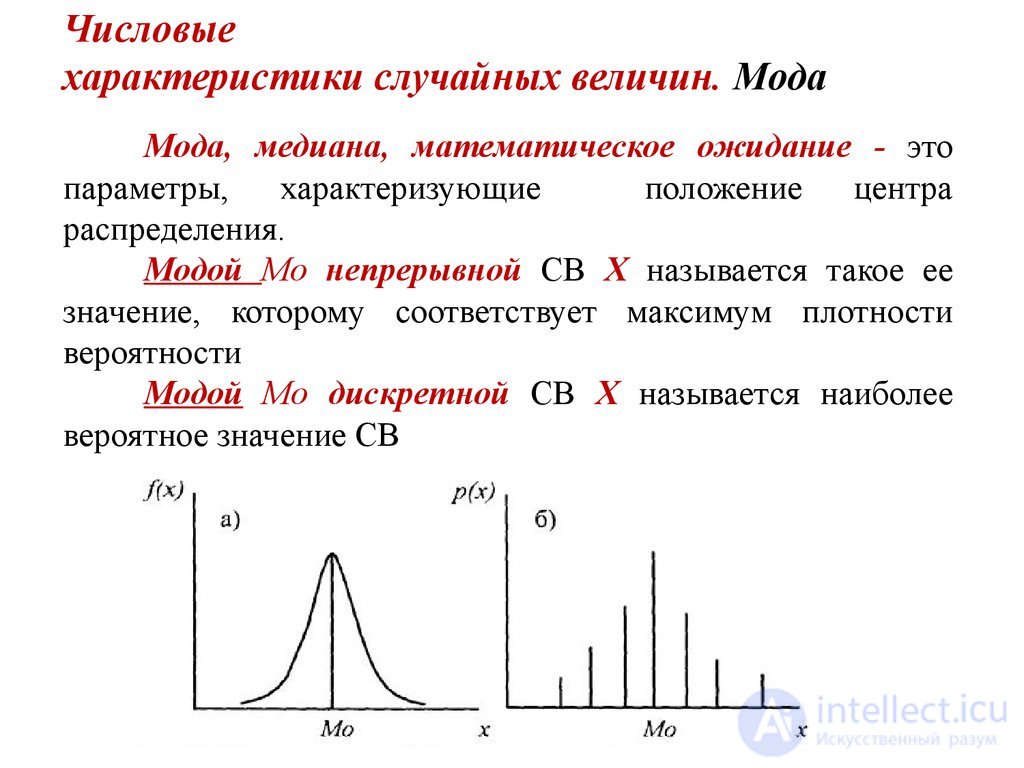
Математическое ожидание, мода, медиана, начальные и центральные моменты и, в частности, дисперсия, среднее квадратическое отклонение, асимметрия и эксцесс представляют собой наиболее употребительные числовые характеристики случайных величин. Во многих задачах практики полная характеристика случайной величины – закон распределения – или не нужна, или не может быть получена. В этих случаях ограничиваются приблизительным описанием случайной величины с помощь. Числовых характеристик, каждая из которых выражает какое-либо характерное свойство распределения.
Медианой Ме непрерывной СВ Х называется такое ее значение, при котором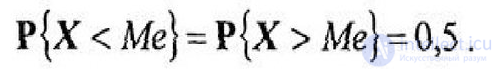 
Можно сказать, что Ме – это такое значение СВ, при котором значение функции обеспеченностей равно значению интегральной функции распределения.
Для дискретных СВ медиана определяется неоднозначно и практически не употребляется.
Очень часто числовыми характеристиками пользуются для приближенной замены одного распределения другим, причем обычно стремятся произвести эту замену так, чтобы сохранились неизменными несколько важнейших моментов.
Математическое ожидание (МО) СВ определяется следующими формулами
МО можно трактовать как центр тяжести плотности вероятности . В качестве символа МО используется обозначение М[Х]. Таким образом, для СВ Х можно записать также mx ~ М[Х]
Математическим ожиданием может называться генеральное среднее, в этом случае для обозначения МО
используется символ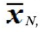 
где N→∞.
Если мода, медиана и математическое ожидание совпадают, то распределение является симметричным.
Если МО расположено правее медианы, то распределение является положительным, в противном случае – отрицательным.
моменты случайной величины Различают начальные и центральные моменты СВ
Начальный момент S – го порядка СВ равен
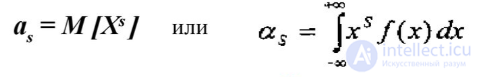
или
Центральный момент пределяется формулой
S-го порядка СВ Х
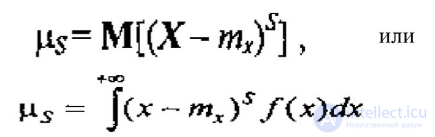
МО - первый начальный момент, то есть
mx = M[X1] = α1
Вторую группу наиболее часто используемых на практике параметров составляют параметры, характеризующие степень рассеяния СВ относительно центра распределения. К ним относится дисперсия, среднеквадратическое отклонение и коэффициент вариации .
Дисперсия СВ Х представляет собой второй центральный момент, то есть
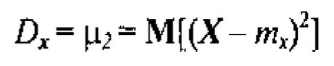
Для непрерывной СВ Х дисперсия определяется формулой
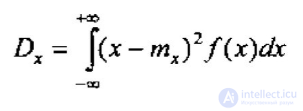
Среднеквадратичное отклонение (СКО) СВ Х (стандарт) это квадратный корень из дисперсии.
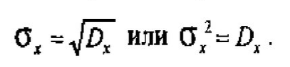
Для описания рассеяния положительных СВ можно использовать безразмерную характеристику – коэффициент вариации.
Коэффициент вариации Сv СВ Х это отношение СКО к МО.
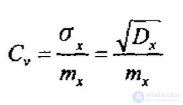
Коэффициент асимметрии С является безразмерным параметром и характеризует степень симметричности рассеяния относительно математического ожидания.
Коэффициент асимметрии определяется формулой
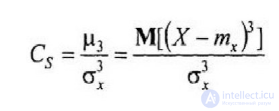
Для симметричных асимметрии равен нулю.
Эксцесс Ех также является безразмерным параметром и определяется формулой
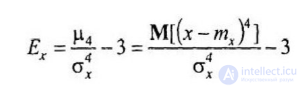
Эксцесс позволяет оценить островершинность, или наоборот туповершинность, функции плотности
вероятности СВ Х относительно нормального закона распределения, для которого Ех =0.
Пример 1. Производится один опыт, в результате которого может появиться или не появиться событие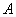 
, вероятность которого равна 
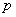. Рассматривается случайная величина – число появлений события 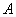(характеристическая случайная величина события 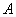). Определить ее характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение.
Решение. Ряд распределения величины имеет вид:
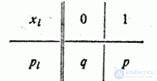
где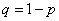 
- вероятность непоявления события .
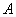По формуле (5.6.1) находим математическое ожидание величины :
.
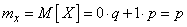Дисперсию величины определяем по формуле (5.7.15):
,
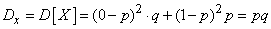откуда
.
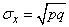(Предлагаем читателю получить тот же результат, выразив дисперсию через второй начальный момент).
Пример 2. Производится три независимых выстрела по мишени; вероятность попадания при каждом выстреле равна 0,4. случайная величина – число попаданий. Определить характеристики величины – математическое ожидание, дисперсию, с.к.о., асимметрию.
Решение. Ряд распределения величины имеет вид:
Вычисляем числовые характеристики величины :
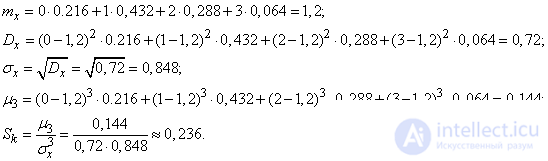
Заметим, что те же характеристики могли бы быть вычислены значительно проще с помощью теорем о числовых характеристиках функций (см. главу 10).
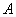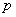Пример 3. Производится ряд независимых опытов до первого появления события (см. пример 3 n° 5.1). Вероятность события в каждом опыте равна . Найти математическое ожидание, дисперсию и с.к.о. числа опытов, которое будет произведено.
Решение. Ряд распределения величины имеет вид:
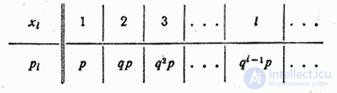
Математическое ожидание величины выражается суммой ряда
.
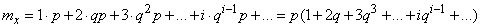Нетрудно видеть, что ряд, стоящий в скобках, представляет собой результат дифференцирования геометрической прогрессии:
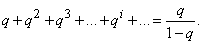
Следовательно,
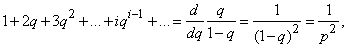
откуда
.
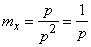Для определения дисперсии величины Х вычислим сначала ее второй начальный момент:
.
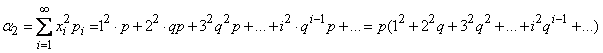Для вычисления ряда, стоящего в скобках, умножим на q ряд:
Получим:
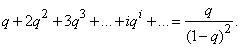
Дифференцируя этот ряд по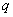 
, имеем:
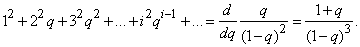
Умножая на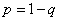 
, получим:
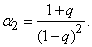
По формуле (5.7.18) выразим дисперсию:
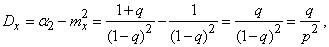
откуда
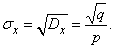
Пример 4. Непрерывная случайная величина подчинена закону распределения с плотностью:
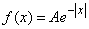
(рис. 5.7.3).
Найти коэффициент 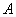. Определить м.о., дисперсию, с.к.о., асимметрию, эксцесс величины .
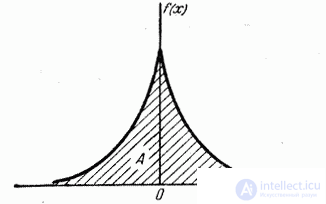
Рис. 5.7.3.
Решение. Для определения 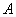воспользуемся свойством плотности распределения:
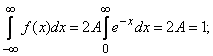
отсюда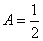 
.
Так как функция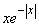 
нечетная, то м.о. величины равно нулю:
.
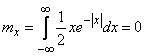Дисперсия и с.к.о. равны, соответственно:
.
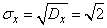Так как распределение симметрично, то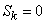 
.
Для вычисления эксцесса находим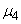 
:
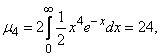
откуда
.
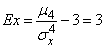Пример 5. Случайная величина подчинена закону распределения, плотность которого задана графически на рис. 5.7.4.
Написать выражение плотности распределения. Найти м.о., дисперсию, с.к.о. и асимметрию распределения.
Рис. 5.7.4.
Решение. Выражение плотности распределения имеет вид:
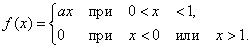
Пользуясь свойством плотности распределения, находим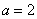 
.
Математическое ожидание величины :
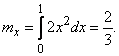
Дисперсию найдем через второй начальный момент:
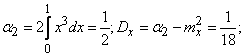
отсюда
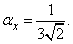
Третий начальный момент равен
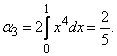
Пользуясь третьей из формул (5.7.10), выражающей 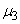через начальные моменты, имеем:
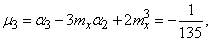
откуда
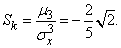
Информация, изложенная в данной статье про моменты случайной величины , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое моменты случайной величины, дисперсия, среднее квадратичное отклонение, коэффициент асимметрии, коэффициент вариации, и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ