Лекция
Привет, сегодня поговорим про случайный процесс, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое случайный процесс , настоятельно рекомендую прочитать все из категории вероятностные процессы.
случайный процесс (вероятностный процесс, случайная функция, стохастический процесс) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.
Другое определение:
Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами.
Пусть дано вероятностное пространство 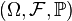 . Параметризованное семейство
. Параметризованное семейство 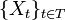 случайных величин
случайных величин
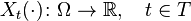 ,
,
где 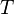 произвольное множество, называется случайной функцией.
произвольное множество, называется случайной функцией.
 , то параметр
, то параметр  может интерпретироваться как время. Тогда случайная функция
может интерпретироваться как время. Тогда случайная функция 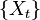 называется случайным процессом. Если множество
называется случайным процессом. Если множество 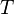 дискретно, например
дискретно, например 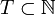 , то такой случайный процесс называется случа́йной после́довательностью.
, то такой случайный процесс называется случа́йной после́довательностью.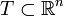 , где
, где 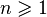 , то параметр
, то параметр  может интерпретироваться как точка в пространстве, и тогда случайную функцию называют случа́йным по́лем.
может интерпретироваться как точка в пространстве, и тогда случайную функцию называют случа́йным по́лем.Данная классификация нестрогая. В частности, термин «случайный процесс» часто используется как безусловный синоним термина «случайная функция».
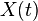 называется процессом дискретным во времени, если система, в которой он протекает, меняет свои состояния только в моменты времени
называется процессом дискретным во времени, если система, в которой он протекает, меняет свои состояния только в моменты времени 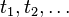 , число которых конечно или счетно. Случайный процесс называется процессом с непрерывным временем, если переход из состояния в состояние может происходить в любой момент времени.
, число которых конечно или счетно. Случайный процесс называется процессом с непрерывным временем, если переход из состояния в состояние может происходить в любой момент времени. , но не от самих значений этих величин. Об этом говорит сайт https://intellect.icu . Другими словами, случайный процесс называется стационарным, если его вероятностные закономерности неизменны во времени. В противном случае, он называется нестационарным.
, но не от самих значений этих величин. Об этом говорит сайт https://intellect.icu . Другими словами, случайный процесс называется стационарным, если его вероятностные закономерности неизменны во времени. В противном случае, он называется нестационарным.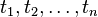 , где
, где 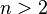 , а
, а 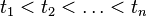 ,случайные величины
,случайные величины 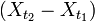 ,
, 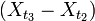 ,
,  ,
,  независимы в совокупности.
независимы в совокупности.Пусть дан случайный процесс 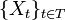 . Тогда для каждого фиксированного
. Тогда для каждого фиксированного 
 — случайная величина, называемая сечением. Если фиксирован элементарный исход
— случайная величина, называемая сечением. Если фиксирован элементарный исход 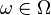 , то
, то 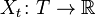 — детерминированная функция параметра
— детерминированная функция параметра 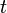 . Такая функция называется траекто́рией или реализа́цией случайной функции
. Такая функция называется траекто́рией или реализа́цией случайной функции 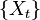 .
.
 , где
, где 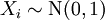 называется стандартной гауссовской (нормальной) случайной последовательностью.
называется стандартной гауссовской (нормальной) случайной последовательностью.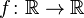 , и
, и  — случайная величина. Тогда
— случайная величина. Тогда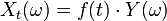
является случайным процессом.
Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной. Случайные функции времени называют случайными процессами.
Реализацией случайной функции X(t) (выборочной функцией) называется конкретный вид, который она принимает в результате опыта. Реализация случайного процесса может рассматриваться как элемент множества возможных физических реализаций случайного процесса (рис. 5.8). Совокупность реализаций случайного процесса называется ансамблем реализаций. Совокупность значений реализаций в фиксированный момент времени (выборка случайных значений) называется сечением случайного процесса.
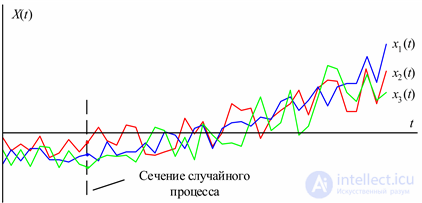
Рис. 5.8. Реализации случайного процесса
В любом сечении случайный процесс есть случайная величина.
Математическое ожидание случайного процесса есть функция времени
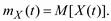 (5.10)
(5.10)
Второй центральный момент для двух сечений случайного процесса называется ковариационной функцией
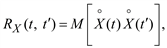 (5.11)
(5.11)
где  – центрированный случайный процесс.
– центрированный случайный процесс.
При t = t′ ковариационная функция равна дисперсии случайного процесса
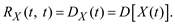 (5.12)
(5.12)
Математическое ожидание и ковариационная функция случайного процесса могут быть найдены по реализациям случайного процесса – осреднением по реализациям:
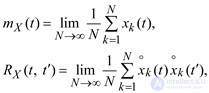 (5.13)
(5.13)
где N – число реализаций случайного процесса.
Если математическое ожидание и ковариационная функция не зависят от времени t, то процесс является стационарным:
 (5.14)
(5.14)
где τ = t′ – t. В (5.14) ковариационная функция зависит только от величины τ, а не от места его расположения на оси времени (рис. 5.9).
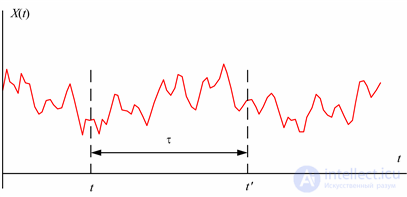
Рис. 5.9. Время между двумя сечениями случайного процесса
Возможный вид ковариационной функции показан на рис. 5.10.
Во многих случаях используется нормированная ковариационная (или корреляционная) функция. Для стационарного случайного процесса
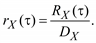 (5.15)
(5.15)
Величина корреляционной функции |rX(τ)| ≤ 1.
Возможно осреднение по времени отдельных выборочных функций (реализаций). Для k-й выборочной функции имеем:
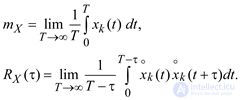 (5.16)
(5.16)
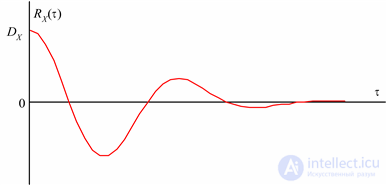
Рис.5.10. Ковариационная функция случайного процесса
Если случайный процесс X(t) стационарен и характеристики mX и RX(τ) одинаковы для различных выборочных функций, то такой процесс называют эргодическим.
Эргодические процессы представляют важный класс случайных процессов.
Нестационарными случайными процессами являются все случайные процессы, не обладающие свойствами стационарности. Эти процессы сложны в исследованиях, и зачастую в задачах по анализу их разбивают на интервалы стационарности или приближенно аппроксимируют стационарными процессами.
Надеюсь, эта статья про случайный процесс, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое случайный процесс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про случайный процесс
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы