Критерий существования процесса с независимыми приращениями. Пуассоновский и винеровский процессы

Привет, мой друг, тебе интересно узнать все про винеровский процесс, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое винеровский процесс, пуассоновский процесс , настоятельно рекомендую прочитать все из категории вероятностные процессы.

Критерий существования процесса с независимыми приращениями в терминах характеристических функций приращений.

§1. В этой главе изучается специальный, но обширный и важный класс
случайных процессов, имеющих независимые приращения. При первом чтении
можно опустить § б о комплекснозначных гауссовских процессах и § 7, в котором
рассматриваются случайные процессы, индексированные семействами функций.
Особое внимание желательно обратить на пуассоновский и винеровский процесс ы
(вводимые в параграфах 2 и 3), широко используемые в последующих главах.
Определение 1. Действительный случайный процесс X = {Xt, t ^ 0} назы-
вается процессом с независимыми приращениями, если для любого п Е N и всех
to, t\,..., tn таких, что 0 = to < ti < • • • < tn, величины Xto, Xtl _L Xto, ...,
Xtn -L Xtn_1 независимы в совокупности.
Теорема 1. Пусть {p(s,t; •)}, где 0 ^ s < t < oo, — семейство характерис-
тических функций, отвечающих некоторому семейству Qs,t, 0 ^ s < t < оо, ве-
роятностных мер на Й§(Е). Для существования случайного процесса X = {Xt,
t ^ 0} с независимыми приращениями такого, что характеристическая функ-
ция случайной величины Xt _L Xs есть (f(s,t; •) при любых 0 ^ s < t < oo,
необходимо и достаточно, чтобы
ф, t; v) = для всех 0^s величины Xq может быть выбрано каким угодно.

Доказательство . Необходимость условия A) очевидна, поскольку характерис-
тическая функция суммы независимых случайных величин равна произведению ха-
рактеристических функций слагаемых.
Пусть теперь выполнено условие A). Допустим, что удалось построить некоторое
вероятностное пространство (П, ^, Р) и искомый процесс X, причем Law(Xo | P) =
= Qo- Тогда характеристическая функция величины Хо равна ристическая функция вектора f = (Xto,Xtl -L Xto,..., Xtn -L Xtn_1) для п e N и
0 = to < h < • • • < tn есть
i,..., Xn) =
Заметим, что
xtl
Xt2
/10 0
1 1 0
111
0
0
X
\1 1 1
1/
t0
xt
tn-1'
Для любого случайного вектора г/ G
ак,т ? М (fc,m = 1,..., q), и всех A Е
, любой матрицы А =
= E ехр{г(Л, Ar,)} = E exp{i{A*X,r1)} = ^(
B)
J>m=1, где
C)
где A* — транспонированная матрица А, (•,•)- скалярное произведение в Жд.
Следовательно, при nGNnO = to самого процесса X должны задаваться характеристическими функциями
где \i — A*Xw A — треугольная матрица, фигурирующая в B): /io = Ао + • • • + Ап,
A*i = Ai H h An, ..., \in — Хп. Кроме того, мы должны иметь M(Pti,...,tn(Ab---5An) =^to5tb...5tn@,Ai,...,An)npHn G NhO < h < ••• < tn.
Итак, предположив существование искомого процесса X, мы выяснили, какие
характеристические функции должны быть у его конечномерных распределений.
Отправляясь от заданных функций ^qo( •) и cp(s, t\ •), где 0 ^ s < t < оо, вве-
дем теперь описанным выше способом характеристические функции iptQ, (Pto,ti,...,tn
и ^tb...,tn @ = ^о < t\ < • • • < tn, n G N) и воспользуемся теоремой 5 главы I.
Условие (а) этой теоремы не требует проверки в силу замечания 3 главы I, а усло-
вие (Ь), точнее, условие (V), означающее подстановку 0 в <рТ(Х) вместо любого ар-
гумента Ат, также выполнено, поскольку согласно A) для 1 ^ т ^ п
; 0
An) =
An).
Тем самым, выполнены условия согласованности и, значит, существование требуе-
мого процесса с независимыми приращениями вытекает из теоремы 5 главы I. Оче-
видно, что распределение Xq будет искомым распределением Qq. ?

Замечание 1. Определение действительного процесса с независимыми прира-
щениями распространяется и на процессы со значениями в Мт (т ^ 1). При этом
теорема 1 остается в силе с незначительной модификацией в ее доказательстве. Так,
в матрицу, фигурирующую в B), вместо единиц следует вписать 1Ш — единичные
матрицы ттг-го порядка, и рассматривать А& Е Mm, к = 0,1,..., т.
Замечание 2. Процесс с независимыми приращениями может быть определен
не только на полупрямой [0, оо). Если Т = N и процесс X = {Xt, t G N} имеет
независимые приращения (т.е. Xt0, Xtx -L Xt0, ..., Xtn -L Xtn_1 независимы для
1 = to < t\ < • • • < tn, где ti G N при i = l,...,nnnGN),TO процесс Х будет иметь
простую структуру: Xt = ?i + • • • + ?t? t ? N, где {^j}'j^1 — последовательность
независимых величин. Тем самым, процессы с независимыми приращениями — ес-
тественное обобщение случайных последовательностей, являющихся суммами не-
зависимых случайных величин.
§ 2. Напомним, что неотрицательная счетно-аддитивная функция m на Зе(Ж) (или
на Й§(М_|_)) называется локально конечной мерой, если m([a,b]) < оо для любых
_Loo < а ^ Ь < оо.
Определение 2. Пуассоновским процессом с ведущей мерой m (где m — ло-
кально конечная мера, ттг(Е) = оо) называется случайный процесс TV = {N(t),t ^ 0}
такой, что
1) jV@) = 0п.н.;
2) процесс N имеет независимые приращения;
3) величины N(t) _L N(s), где 0 ^ s < t < оо, распределены по закону Пуассона
с параметром m((s,t]).
В частности, если m((s, i\) = (t _L s)A, 0 ^ s < t < oo, A > 0, то говорят о стан-
дартном пуассоновском процессе с постоянной интенсивностью А.
Условимся считать, что пуассоновское распределение с нулевым параметром име-
ет случайная величина, тождественно равная нулю.
Существование пуассоновского процесса следует из теоремы 1. Действительно,
если бы такой процесс имелся, то согласно 3) мы получили бы
ф,Ци) = Для так определенной функции cp(s,t;u), O^s полнено, поскольку m((s,t]) = m((s, и]) + т((и, ?]), что позволяет воспользоваться
теоремой 1. В качестве начального распределения Qo надо взять меру, сосредото-
ченную в точке 0.
Следующий результат интересен тем, что объясняет как устроены траектории
пуассоновского процесса.
Теорема 2 (явная конструкция пуассоновского процесса). Пусть ?i, ?2 ? • • • —
независимые случайные величины, имеющие экспоненциальное распределение
с плотностью
^ х > О,
х<0, D)
где А — положительный параметр, г G N. Тогда соответствующий процесс
восстановления A.10) является пуассоновским процессом интенсивности А.

Эта теорема не доказывается, поскольку она есть частный случай общего пост-
роения марковских цепей с помощью инфинитезималъной матрицы (см. упражне-
ние 33 главы VI).
Пример 1. Пусть процесс Y = [Yt,t ^ 0} определяется согласно формуле A.11),
где величины ?i, ?2? • • • имеют показательное распределение с параметром Л > 0.
Покажем, что процесс Y имеет независимые приращения.
Заметим, что если Z = {Zt, t ^ 0} — действительный процесс с независимы-
ми приращениями и h = h{t) — неслучайная действительная функция на [0, оо), то
{Zt + h(t), t ^ 0} — также процесс с независимыми приращениями. Поэтому про-
цесс Y (см. A.11)) будет иметь независимые приращения, если этим свойством обла-
xt
дает S = {St, t ^ 0}, где St = Yl Vj- В силу теоремы 2 процесс X = {Xt, t ^ 0},
задаваемый формулой A.10), является пуассоновским процессом интенсивности Л.
Положим ф(у) = Е elvril, v G Е. Учитывая независимость приращений пуассо-
новского процесса, а также независимость последовательностей {?j}j^n и {
(т. е. независимость порожденных ими сг-алгебр), имеем для 0^s к,т=0
оо
k,m=O
СЮ СЮ / л / j I \ \
V Р(Х =к)У^ (фA'))ш^ ^
к=0 т=0
Vj\P(Xs=k)P(Xt±Xs=m) =
Аналогично вычисляется совместная характеристическая функция набора прираще-
ний процесса {St, t ^ 0}, откуда следует требуемое утверждение.

Пуассоновский и винеровский процессы

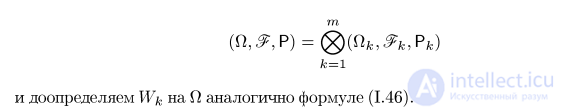
Винеровский процесс в теории случайных процессов — это математическая модель броуновского движения или случайного блуждания с непрерывным временем.

Случайный процесс , где называется винеровским процессом, если

1. почти достоверно.
2. — процесс с независимыми приращениями.
3. , ,

где – нормальное распределение со средним и дисперсией . Величину , постоянную для процесса, далее будем считать равной .

Эквивалентное определение:

1. – гауссовский процесс.
2. , .
3. , .

Непрерывность траекторий

Существует единственный винеровский процесс такой, что почти все его траектории всюду непрерывны. Об этом говорит сайт https://intellect.icu . Поскольку обычно рассматривают именно этот процесс, то часто условие непрерывности траекторий включают в определение винеровского процесса.

Свойства винеровского процесса

• — гауссовский процесс.
• — марковский процесс.
• . Соответственно и .

• .
• - мартингал. Здесь под мартингалом мы понимаем
• Если — винеровский процесс, то и , также будет винеровским.

• Винеровский процесс масштабно инвариантен или самоподобен. Если — винеровский процесс, и , то

также является винеровским процессом.

• Корреляционная функция для производной винеровского процесса является дельта-функцией.

• Траектории винеровского процесса нигде не дифференцируемы почти наверное. Производная (в обобщенном смысле) винеровского процесса — нормальный белый шум.

• Для любого заданного отрезка траектории винеровского процесса — функции неограниченной вариации на этом отрезке почти наверное.

• Для винеровского процесса справедлив закон повторного логарифма.

почти наверное.

• 

Многомерный винеровский процесс

Многомерный (-мерный) винеровский процесс — это -значный случайный процесс, составленный из независимых одномерных винеровских процессов, то есть

,

где процессы совместно независимы.

Связь с физическими процессами

Винеровский процесс описывает броуновское движение частицы, совершающей беспорядочные перемещения под влиянием ударов молекул жидкости. Константа при этом зависит от массы частицы и вязкости жидкости.

Процесс Пуассона

Процесс Пуассона, поток Пуассона, пуассоновский процесс — ординарный поток однородных событий, для которого число событий в интервале А не зависит от чисел событий в любых интервалах, не пересекающихся с А, и подчиняется распределению Пуассона. В теории случайных процессов описывает количество наступивших случайных событий, происходящих с постоянной интенсивностью.

Вероятностные свойства потока Пуассона полностью характеризуются функцией Λ(А), равной приращению в интервале А некоторой убывающей функции. Чаще всего поток Пуассона имеет мгновенное значение параметра λ(t) — функцию, в точках непрерывности которой вероятность события потока в интервале [t,t+dt] равна λ(t)dt. Если А — отрезок [a,b], то

Поток Пуассона, для которого λ(t) равна постоянной λ, называется простейшим потоком с параметром λ.

Потоки Пуассона определяются для многомерного и вообще любого абстрактного пространства, в котором можно ввести меру Λ(А). Стационарный поток Пуассона в многомерном пространстве характеризуется пространственной плотностью λ. При этом Λ(А) равна объему области А, умноженному на λ.

Классификация процессов Пуассона:

Различают два вида процессов Пуассона: простой (или просто: процесс Пуассона) и сложный (обобщенный).

Простой процесс Пуассона

Пусть . Случайный процесс называется однородным Пуассоновским процессом с интенсивностью , если

1. почти наверное.
2. — процесс с независимыми приращениями.
3. для любых , где обозначает распределение Пуассона с параметром .

Сложный (обобщенный) пуассоновский процесс

• Пусть последовательность взаимно независимых одинаково распределенных случайных величин.
• Пусть — простой пуассоновский процесс с интенсивностью , не зависящий от последовательности .

Обозначим через сумму первых k элементов введенной последовательности.

Тогда определим сложный Пуассоновский процесс как .

Свойства процессов Пуассона:

• Времена между моментами скачков независимы и имеют экспоненциальное распределение .
• Пуассоновский процесс принимает только неотрицательные целые значения, и более того

,

то есть момент -го скачка имеет гамма-распределение .

• Траектории процесса Пуассона — кусочно-постоянные, непрерывные справа, неубывающие функции со скачками равными единице почти наверное. Более точно

при ,

где обозначает «о малое».

Критерий

Для того чтобы некоторый случайный процесс с непрерывным временем был пуассоновским (простым, однородным) или тождественно нулевым достаточно выполнение следующих условий:

1. .
2. Процесс имеет независимые приращения.
3. Процесс однородный.
4. Процесс принимает целые неотрицательные значения.
5. при .

Информационные свойства процессов Пуассона:

• Пусть — моменты скачков процесса Пуассона. .

Зависит ли от предыдущей части траектории?
— ?

Пусть .

.
Распределение длин промежутков времени между скачка́ми обладает свойством отсутствия памяти ⇔ оно показательно.

• Рассмотрим отрезок на временно́й оси.

— число скачков на отрезке .
Условное распределение моментов скачков совпадает с распределением вариационного ряда, построенного по выборке длины из .

Плотность этого распределения

Центральная предельная теорема

• Теорема.

Скорость сходимости:
,
где — константа Берри-Эссеена.

Применение процессов Пуассона:

Поток Пуассона служит для моделирования различных реальных потоков: несчастных случаев, потока заряженных частиц из космоса, отказов оборудования и других. Так же возможно применение для анализа финансовых механизмов, таких как поток платежей и других реальных потоков. Для построения моделей различных систем обслуживания и анализа их пригодности.

Использование потоков Пуассона значительно упрощает решение задач систем массового обслуживания, связанных с расчетом их эффективности. Но необоснованная замена реального потока потоком Пуассона там, где это недопустимо, приводит к грубым просчетам.

§ 3. Введем один из самых важных случайных процессов.
Определение 3. Винеровским процессом, или броуновским движением, на-
зывается случайный процесс W = {W(t), t ^ 0} такой, что
1) W@) = 0п.н.;
2) процесс W имеет независимые приращения;
3) величины W(t) _L W(s) ~ N@, t _L s) при всех 0 ^ s < t < 00, т. е. величины
W(t) _L W(s) имеют гауссовское (нормальное) распределение с параметрами
Существование процесса, обладающего свойствами 1)-3), вытекает из теоремы 1,
поскольку
, (t-s)u2 , (u-s)u2 , (t-u)u2
е^ 2 = е^ 2 е^ 2 , 0 ^ s < и < ?, v G Е,
что обеспечивает выполнение условия A).
50 А. В. Булинский, А. Н. Ширяев
Для винеровского процесса W(t) = W(t) _L W@) ~ N@,?), поэтому EW(t) = 0
при всех t ^ 0. Если 0 ^ s ^ ?, то ковариация
cov(W(s), W(t)) = cov(W(s), W(?) _L W(s) + W(s)) = D(W(s) _L W@)) = 5,
где D обозначает дисперсию. Тем самым, для винеровского процесса W
EW(t)=0, cov(W(s),W(t)) = min{s,?} при s,t e[0,oo). F)
Замечание 3. Обычно в определение винеровского процесса включают еще тре-
бование непрерывности п. н. (т. е. непрерывности с вероятностью единица) его тра-
екторий. Далее мы увидим, что это свойство действительно всегда можно считать
выполненным наряду со свойствами 1)-3).
Определение 4. Многомерным (m-мерным) броуновским движением W =
= {W(?) = (Wi(t),..., Wm(t)), t ^ 0} называется процесс со значениями в Ет, со-
ставленный из т независимых (непрерывных) броуновских движений {Wk(t), t^O},
к = 1,... ,?тг.
Независимость процессов в этом определении понимается как независимость по-
рожденных ими сг-алгебр (см. замечание 1 главы I). Такой процесс W легко получим,
задав на некоторых вероятностных пространствах (П&, ^, P&), к = 1,..., ттг, соот-
ветствующие броуновские движения Wk = {Wk(t), t ^ 0}. Далее берем
к=1
и доопределяем Wk на П аналогично формуле A.46).

Вау!! 😲 Ты еще не читал? Это зря!

• Сосиска Винера
• Норберт Винер
• Формула Фейнмана — Каца
• Цвета шума
• Поток однородных событий
• Теория массового обслуживания

Напиши свое отношение про винеровский процесс. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое винеровский процесс, пуассоновский процесс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы

Из статьи мы узнали кратко, но содержательно про винеровский процесс