Лекция
Привет, сегодня поговорим про марковский процесс, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое марковский процесс , настоятельно рекомендую прочитать все из категории вероятностные процессы.
марковский процесс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра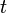 
не зависит от эволюции, предшествовавшей 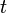, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»).
Процесс Маркова — модель авторегрессии первого порядка AR(1): xt=ψ1*xt-1+εt
Случайный процесс, протекающий в системе, называется марковским, если он обладает отсутствием последствия. Т.е. если рассматривать текущее состояние процесса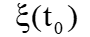 
- как настоящее, совокупность возможных состояний 
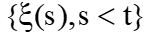- как прошлое, совокупность возможных состояний 
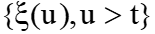- как будущее, то для марковского процесса при фиксированном настоящем будущее не зависит от прошлого, а определяется лишь настоящим и не зависит от того, когда и как система пришла в это состояние.
Марковские случайные процессы названы по имени выдающегося русского математика А.А.Маркова, впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать "динамикой вероятностей". В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д.
Определяющее марковский процесс свойство принято называть марковским; впервые оно было сформулировано А. А. Марковым, который в работах 1907 г. положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин. Это направление исследований известно под названием теории цепей Маркова.
Однако уже в работе Л. Башелье можно усмотреть попытку трактовать броуновское движение как марковский процесс, попытку, получившую обоснование после исследований Винера в 1923.
Основы общей теории марковских процессов с непрерывным временем были заложены Колмогоровым.
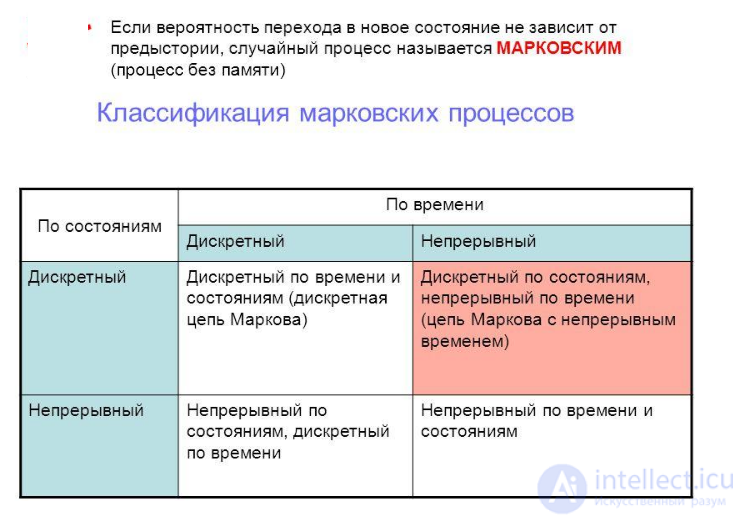
Марковская цепь с дискретным временем — время дискретно, пространство состояний дискретно.
Марковская цепь с непрерывным временем — время непрерывно, пространство состояний дискретно.
Марковский процесс — и время, и пространство состояний непрерывно.
Пусть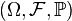 
— вероятностное пространство с фильтрацией 
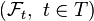по некоторому (частично упорядоченному) множеству 
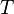; и пусть 
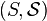— cигма-алгебра. Об этом говорит сайт https://intellect.icu . Случайный процесс 
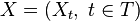, определенный на фильтрованном вероятностном пространстве, считается удовлетворяющим марковскому свойству, если для каждого 
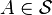и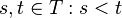 
,
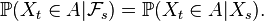
Марковский процесс — это случайный процесс, удовлетворяющий марковскому свойству с естественной фильтрацией.
В случае, если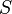 
является дискретным множетсвом и 
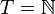, определение может быть переформулировано:
.
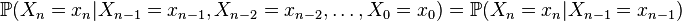Рассмотрим простой пример марковского случайного процесса. По оси абсцисс случайным образом перемещается точка. В момент времени ноль точка находится в начале координат и остается там в течение одной секунды. Через секунду бросается монета — если выпал герб, то точка X перемещается на одну единицу длины вправо, если цифра — влево. Через секунду снова бросается монета и производится такое же случайное перемещение, и так далее. Процесс изменения положения точки («блуждания») представляет собой случайный процесс с дискретным временем (t=0, 1, 2, …) и счетным множеством состояний. Такой случайный процесс называется марковским, так как следующее состояние точки зависит только от настоящего (текущего) состояния и не зависит от прошлых состояний (неважно, каким путем и за какое время точка попала в текущую координату).
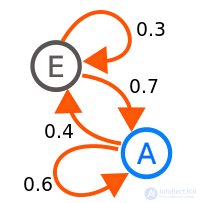
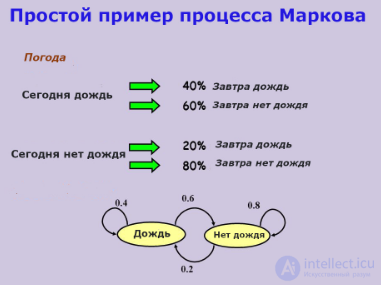
Диаграмма, представляющая марковский процесс с двумя состояниями, с состояниями, обозначенными E и A. Каждое число представляет вероятность перехода марковского процесса из одного состояния в другое в направлении, указанном стрелкой. Например, если марковский процесс находится в состоянии A, то вероятность, что он перейдет в состояние E, равна 0,4, а вероятность, что он останется в состоянии A, равна 0,6.
Система S – группа самолетов, участвующих в воздушном бою. Пусть x – количество «красных» самолетов, y – количество «синих» самолетов. К моменту времени t0 количество сохра-нившихся (не сбитых) самолетов соответственно – x0, y0.
Нас интересует вероятность того, что в момент времени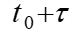 
численный перевес будет на стороне «красных». Эта ве-роятность зависит от того, в каком состоянии находилась си-стема в момент времени t0, а не от того, когда и в какой после-довательности погибали сбитые до момента t0 самолеты
На практике марковские процессы в чистом виде обычно не встречаются. Но имеются процессы, для которых влиянием «предыстории» можно пренебречь, и при изучении таких процессов можно применять марковские модели. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях.
Надеюсь, эта статья про марковский процесс, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое марковский процесс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про марковский процесс
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы