2.12. Альтернирующие процессы восстановления кратко

Привет, Вы узнаете о том , что такое альтернирующие процессы восстановления , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое альтернирующие процессы восстановления , настоятельно рекомендую прочитать все из категории вероятностные процессы.

2.12. альтернирующие процессы восстановления

ОПРЕДЕЛЕНИЕ 2.3. Альтернирующим процессом восстановления называется поток с ограниченным последействием, у которого

F_2k-1(t)=F(t), F_2k(t)=G(t), k=1,2,3,..., F(t)≠ G(t). (2.64)

Таким образом, альтернирующий процесс восстановления задается распределением F(x) нечетных интервалов и распределением G(x) четных интервалов между соседними моментами восстановления.

Нетрудно заметить, что поток четных восстановлений альтернирующего процесса образует простой процесс восстановления с распределением интервалов, равным свертке распределений F(t) и G(t),

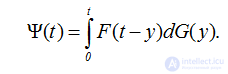(2.65)

Поток нечетных восстановлений альтернирующего процесса образует процесс восстановления с запаздыванием, определяемый функциями F(t) и Ψ(t).

Обозначим H₀(t) и H₁(t) функции восстановления этих потоков и H(t)=H₀(t)+H₁(t) функцию восстановления альтернирующего процесса. Об этом говорит сайт https://intellect.icu . В силу (2.16) и (2.19)

• 

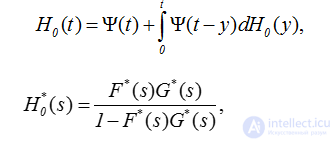
  поскольку Ψ^*(s)=F^*(s)G^*(s).

  Из равенств (2.17) и (2.20) получаем
  

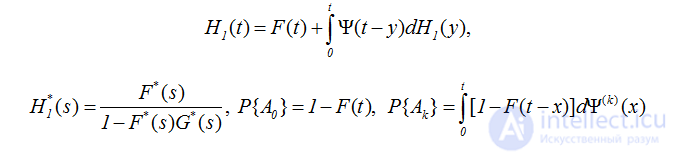
  и, следовательно,

• 

  Если воспользоваться равенствами (2.22) и (2.53), то получим
  

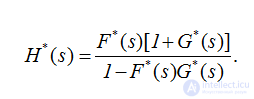
  Следовательно, для функции восстановления альтернирующего процесса восстановления будем иметь следующее асимптотическое разложение

• 

  Далее исследуем вероятность того, что произвольный момент t>0 накрывается нечетным интервалом восстановления. Для этого введем в рассмотрение следующие события

  .

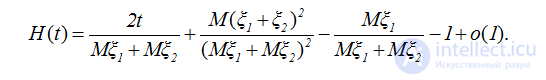
  Тогда событие A, состоящее в том, что момент t накрывается нечетным интервалом восстановления, можно записать как сумму несовместных событий A_k, т.е. . Поэтому

  .

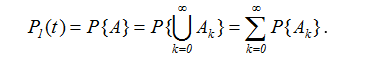
  Так как 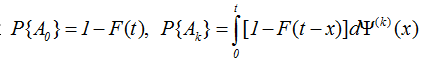при k>0, то

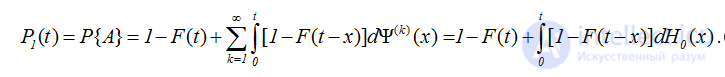  .(2.66)

  Для вероятности P₂(t) противоположного события - момент t накрывается четным интервалом справедливо равенство

  ,

  (2.67)

  если провести рассуждения, аналогичные рассуждениям, проведенным при выводе (2.66), для альтернирующего процесса как процесса восстановления с запаздыванием.

  Равенства (2.66) и (2.67) используем для исследования предела lim_t→∞P_n(t), n=1,2. Для определения предела интеграла воспользуемся узловой теоремой восстановления. Если хотя бы одно распределение F(x) или G(x) нерешетчатое и существуют их математические ожидания, то пределы существуют и

  (2.68)

Вау!! 😲 Ты еще не читал? Это зря!

• Случайная мера Пуассона
• случайный процесс
• случайные блуждания
• процесс восстановления
• модель Крамера-Лундберга
• эмпирические меры
• пуассоновская случайная мера

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области альтернирующие процессы восстановления имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое альтернирующие процессы восстановления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы