Лекция
Привет, Вы узнаете о том , что такое интегральные уравнения восстановления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое интегральные уравнения восстановления , настоятельно рекомендую прочитать все из категории вероятностные процессы.
Теперь воспользуемся равенствами (2.4) и (2.10) для вывода интегральных уравнений восстановления.
С этой целью напомним понятие k-кратной свертки, которая определяется рекуррентно,
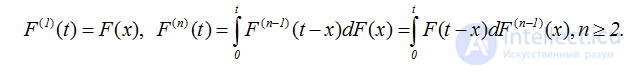(2.13)
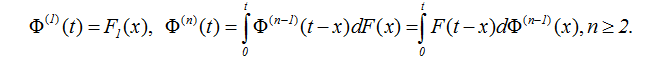(2.14)
Кроме равенств (2.14), для сверток можно предложить другую форму записи через свертки F(n)(t)
. 
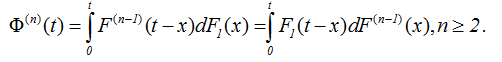(2.15)
Коль скоро, ряды (2.4) и (2.10) сходятся равномерно на любом конечном интервале, то можно переставлять порядок суммирования и интегрирования.
Тогда, суммируя равенства (2.13), получаем
.
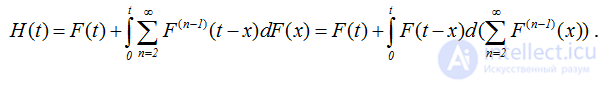
В силу того, что , получаем два интегральных уравнения для функции восстановления простого процесса восстановления
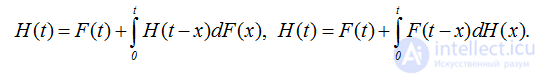(2.16)
Нетрудно заметить, что интегрированием по частям одно уравнение можно получить из другого.
Суммируя равенства (2.14), получаем два интегральных уравнения для функции восстановления процесса восстановления с запаздыванием
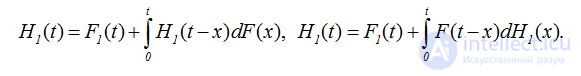(2.17)
Наконец, суммируя равенства (2.15), получаем соотношения, связывающие функции восстановления H1(t) и H(t),
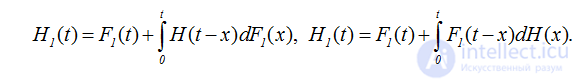(2.18)
Решения уравнений восстановления можно выписать, используя преобразование Лапласа-Стилтьеса , Res>0.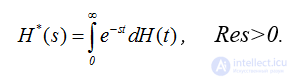 
Известно (математическое приложение 2), что преобразование Лапласа-Стилтьеса интеграла свертки равно произведению преобразований Лапласа-Стилтьеса. Об этом говорит сайт https://intellect.icu . Поэтому из (2.16) получаем
. 
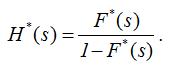(2.19)
Аналогично из (2.17) получаем для процесса восстановления с запаздыванием
. 
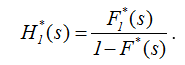(2.20)
Формулы (2.19) и (2.20) используются для определения функций H(t) и H1(t), для чего надо обратить преобразования H*(s) и H1*(s), то есть найти такие функции H(t) и H1(t), у которых заданные преобразования H*(s) и H1*(s). Так как существует взаимно однозначное соответствие между функциями и их преобразованиям Лапласа-Стилтьеса, то найденные H(t) и H1(t) будут единственными решениями интегральных уравнений восстановления.
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области интегральные уравнения восстановления имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое интегральные уравнения восстановления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про интегральные уравнения восстановления
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы