Лекция
Привет, мой друг, тебе интересно узнать все про интеграл ито, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое интеграл ито, стохастическое исчисление ито, стохастический интеграл, интеграл винера, интеграл стратоновича , настоятельно рекомендую прочитать все из категории вероятностные процессы.
стохастический интеграл — интеграл вида 
, где 
— случайный процесс с независимыми нормальными приращениями. Стохастические интегралы широко используются в стохастических дифференциальных уравнениях. Стохастический интеграл нельзя вычислять как обычный интеграл Стилтьеса.
Стохастический интеграл можно определить при помощи сумм 
. Интеграл получается, как и у интеграла Стилтьеса, переходом к пределу: 
.
Рассмотрим интеграл 
, где 
— винеровский процесс с единичным параметром дисперсии. Разделим интервал 
точками 
на 
подинтервалов. Используя предыдущее определение интеграла для детерминированной функции, стохастический интеграл можно определить любым из двух выражений: 
, или 
. Эти интегралы не равны, поскольку, по определению винеровского процесса: 
. Обобщенный стохастический интеграл можно определить как взвешенную по параметру 
сумму интегралов 
и 
следующей формулой: 
, при 
. Об этом говорит сайт https://intellect.icu . Интеграл соответствует интегралу Ито, а 
совпадает с интегралом Стратоновича.
Интеграл Стратоновича имеет вид: 
.
Интеграл Ито имеет вид: 
. Его основные свойства: 
, 
.
Сформулируем некоторые его свойства:
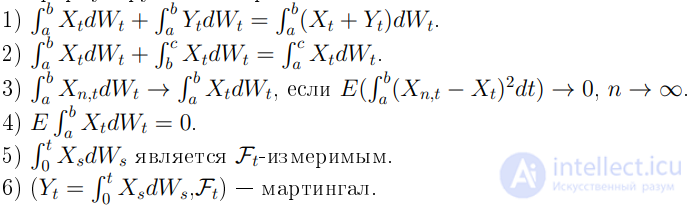
Поставим в соответствие каждой траектории одномерного винеровского процесса некоторое число 
. Тогда эту траекторию можно описать посредством стохастической функции 
. Интеграл вида 
называется стохастическим интегралом Винера. Этот интеграл вычисляется аналогично интегрированию по частям: 
. Его основные свойства: 
, 
.
Исчисление Ито — математическая теория, описывающая методы манипулирования со случайными процессами, такими как броуновское движение (или винеровский процесс). Названа в честь создателя, японского математика Киеси Ито. Часто применяется в финансовой математике и теории стохастических дифференциальных уравнений. Центральным понятием этой теории является интеграл Ито
записывающийся также в виде 
, где 
— броуновское движение или, в более общей формулировке, полумартингал. Можно показать, что путь интегрирования для броуновского движения нельзя описать стандартными техниками интегрального исчисления. В частности, броуновское движение не является интегрируемой функцией в каждой точке пути и имеет бесконечную вариацию по любому временному интервалу. Таким образом, интеграл Ито не может быть определен в смысле интеграла Римана — Стилтьеса. Однако, интеграл Ито можно определить корректно, если заметить, что подынтегральная функция 
есть адаптивный процесс; это означает, что зависимость от времени 
его среднего значения определяется поведением только до момента .
где 
, 
- последовательность разбиений интервала [0, t] с длиной подынтервалов стремящейся к нулю.
and 
Я хотел бы услышать твое мнение про интеграл ито Надеюсь, что теперь ты понял что такое интеграл ито, стохастическое исчисление ито, стохастический интеграл, интеграл винера, интеграл стратоновича и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про интеграл ито
Комментарии