Лекция
Привет, мой друг, тебе интересно узнать все про дифференциальные уравнения колмогорова , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое дифференциальные уравнения колмогорова , настоятельно рекомендую прочитать все из категории вероятностные процессы.
дифференциальные уравнения колмогорова (УрК) служат для описания изменчивости вероятностей состояний многоэлементной системы с отказами и восстановлениями.
При этом предполагают, что система функционирует в непрерывном времени, а ее элементы меняют свое состояние под воздействием дискретных токов отказов и восстановлений с интенсивностями k и µk соответственно; здесь k = 1,…, m , где m – число элементов системы. При простейшем потоке этих событий, т. е. при ординарности потока и отсутствии последействия, возникает марковский процесс переходов системы из состояния в состояние. УрК описывают подобные процессы.
Переменными в УрК служат вероятности состояний исследуемой системы (t), . Получение этих вероятностей в результате решения УрК позволяет оценить практически важные показатели надежности, например, вероятность безотказной работы системы.
Существуют определенные правила формирования УрК. Предварительно многоэлементную систему удобно представить в виде графа состояний. Для этого указывают его вершины (состояния с их вероятностями ) и дуги (ребра) с пометками k или µk , учитывающими переходы из состояния в состояние под воздействием потоков отказов или восстановлений элементов системы.
Каждое i-ое уравнение в составе УрК записывается так:
Сформированная подобным образом система УрК в векторноматричной форме имеет вид:

где A – (n × n)-матрица коэффициентов; P – (n × 1)-вектор вероятностей Pi состояний исследуемой системы; P0 – вектор начальных условий.
Особенностью УрК (1) является вырожденность матрицы А, поэтому попытка интегрировать систему уравнений (1) без предварительного преобразования обречена на неудачу.
Вырожденность А определяется наличием линейной связи элементов вектора Р в виде очевидного равенства:
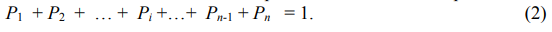
Из (2) следует, что сумма всех уравнений в системе (1) даст ноль, что возможно лишь при условии (вектор Р в общем случае ненулевой): сумма строк матрицы А есть нулевая строка. Об этом говорит сайт https://intellect.icu . Это утверждение свидетельствует о наличии линейной зависимости строк матрицы А и объясняет причину ее вырожденности. При желании данное утверждение можно использовать в качестве критерия корректности формирования матрицы А.
Легко убедиться в том, что собственные числа (с.ч.) матрицы А – вещественные, причем (n – 1) этих с.ч. – отрицательные, а одно с.ч. – нулевое. Отсюда следует, что проблема определения вектора Р может быть решена снижением числа уравнений (1) на единицу, используя (2). Из (2) можно выразить любую переменную через остальные.
Выполним это преобразование исключением из (1) последнего элемента вектора Р:
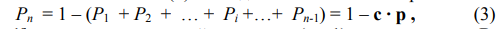
где р – [(n – 1) × 1]-вектор, составленный из первых (n - 1) членов вектора Р; с – [1 × (n – 1)]-строка, состоящая из единиц:

После преобразований получим (n – 1) первых системы (1) в виде:

где R – [(n – 1) × (n – 1)]-верхний диагональный блок матрицы А; b – [(n – 1) × 1]-вектор, составленный из первых (n - 1) членов n-го (последнего) столбца матрицы А. Матрица М – невырожденное ядро матрицы А, поэтому показателем корректности преобразований служит совпадение с.ч. матрицы М и ненулевых с.ч. матрицы А.
Уравнения (5) теперь могут быть использованы при решении прикладных задач анализа характеристик надежности как в динамике, так и в статике (при t → ∞). В любом случае из уравнений (5) определяются (n - 1) первых элементов вектора Р; последний, ранее исключенный из УрК, элемент Pn находится из выражения (3). Анализ динамики изменения вероятностей состояний осуществляется интегрированием уравнений (5). Установившееся значение этих вероятностей находится из следующего соотношения:

При решении прикладных задач анализа многоэлементных систем с отказами и восстановлениями с использованием УрК могут быть решены так называемые прямые и обратные задачи. Прямая задача предполагает анализ вероятностей состояний и характеристик надежностей при задании конкретных значений интенсивностей.
Решение обратной задачи предполагает нахождение интенсивности отказов и/или восстановлений с использованием одного из возможных критериев, наприер, максимизацией вероятности безотказной работы.
Напиши свое отношение про дифференциальные уравнения колмогорова . Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое дифференциальные уравнения колмогорова и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про дифференциальные уравнения колмогорова
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы