Привет, мой друг, тебе интересно узнать все про стационарные в широком смысле процессы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое стационарные в широком смысле процессы , настоятельно рекомендую прочитать все из категории вероятностные процессы.

стационарные в широком смысле процессы , их спектральное представление. Эргодичность в L2().

Важным классом случайных процессов являются стационарные случайные процессы, то есть, случайные процессы, не изменяющие свои характеристики с течением времени. Они имеют вид непрерывных случайных колебаний вокруг некоторого среднего значения. Таковыми являются: давление газа в газопроводе, колебания самолета при «автополете», колебания напряжения в электрической сети и т.д.

Случайный процессназываетсястационарным в широком смысле,если его математическое ожидание есть постоянное число, а корреляционная функциязависит только от разности аргументов, т.е.

Из этого определения следует, что корреляционная функция стационарного процесса есть функция одного аргумента: Это обстоятельство часто упрощает операции над стационарными случайными процессами.

Случайный процесс называют стационарным в узком смысле, если его характеристики зависят не от значений аргументов, а лишь от их взаимного расположения. То есть, для функции распределения сечений процесса должно выполняться равенство:

при любых

Отметим, что из стационарности СП в узком смысле следует стационарность его в широком смысле, обратное утверждение неверно.

В дальнейшем мы будем рассматривать только стационарные случайные процессы в широком смысле. Далее приведем основные свойства корреляционной функции случайного стационарного процесса (с.с.п.).

1. Дисперсия с.с.п. постоянна и равна значению корреляционной функции в нуле, т.е.

, то есть в начале координат.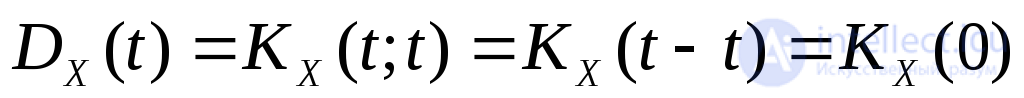

2. Корреляционная функция с.с.п. является четной функцией, т.е.

3. Абсолютное значение корреляционной функции с.с.п. не превосходит ее значение при 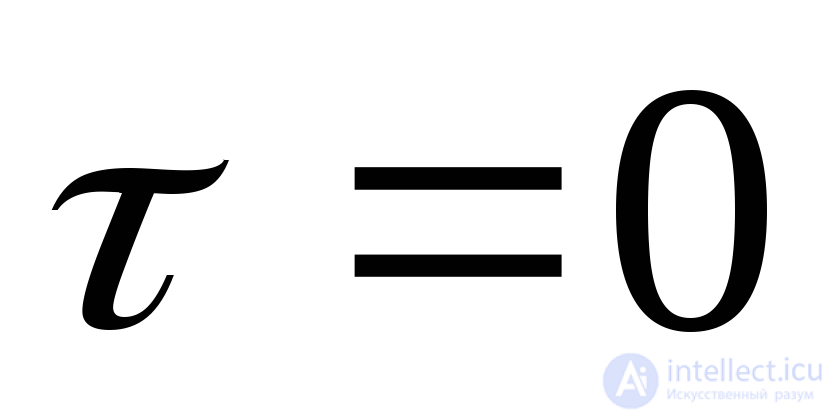, т.е.

Нормированная корреляционна функция с.с.п. является неслучайная функция аргумента , т.е.

при этом в соответствии свойство 3 имеет место неравенство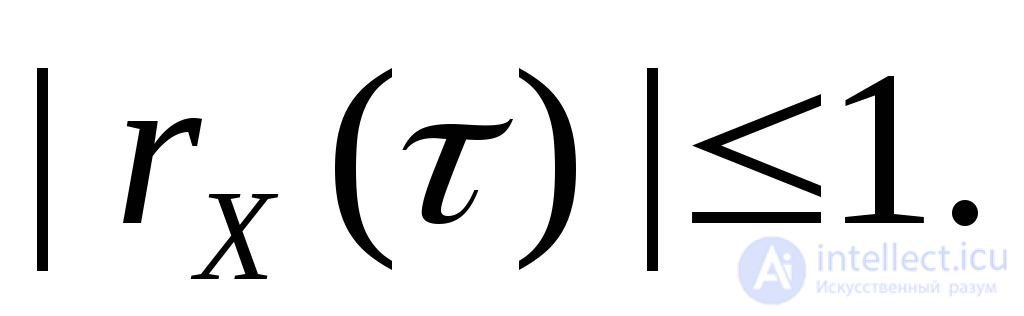

Пример 6. Задана случайная функция,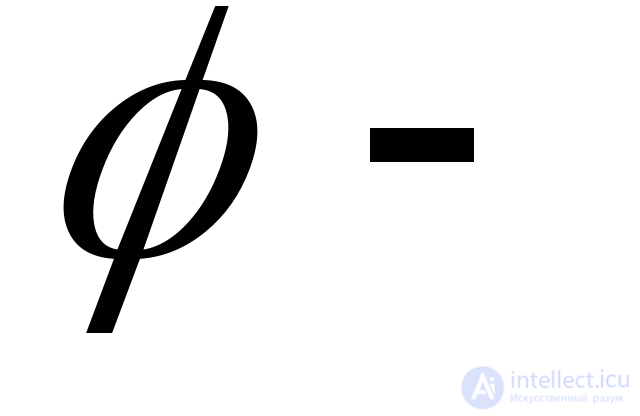равномерно распределенная случайная величина, в интервале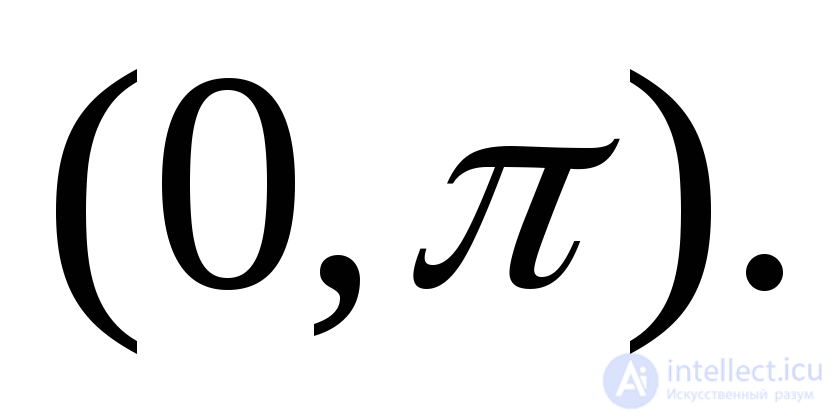

Доказать, что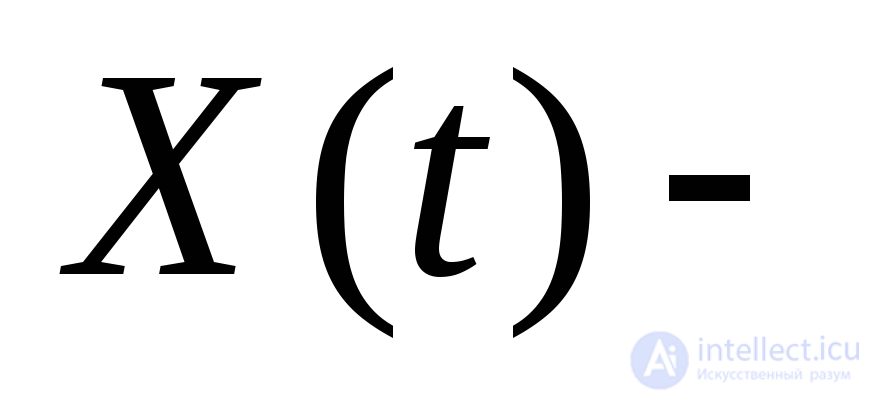случайная стационарная функция.

Решение. Найдем математическое ожидание

.

На основании определения м.о. получим (с учетом равномерной распределенности с.в. , по условию контроля)

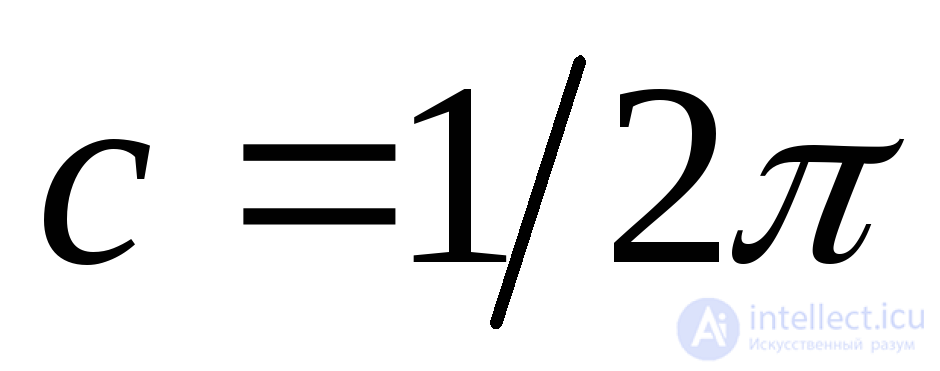и

Следовательно,

Найдем корреляционную функцию. Учитывая, что центрированная и случайная функция равны (т.к. ), т.е., то согласно определению корреляционной функции (см.пункт 16.5) имеем

.

,

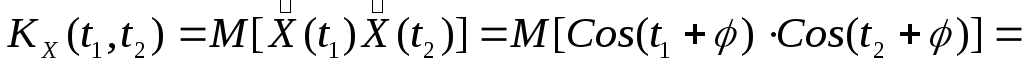
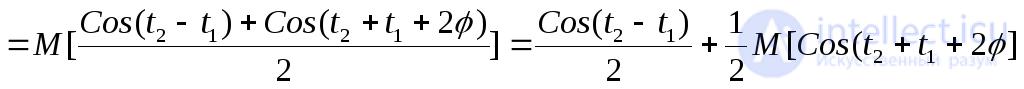поскольку ).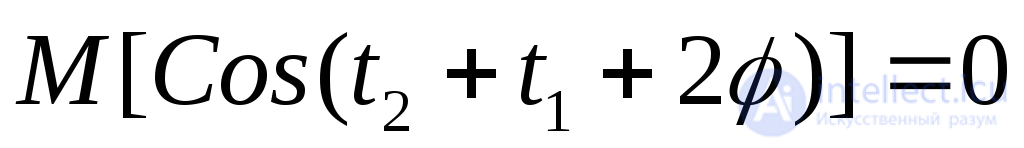

Задание. Покажите, что в условиях нашего примера имеет место

Итак, математическое ожидание с.в. Об этом говорит сайт https://intellect.icu . есть постоянное число при всех значениях аргумента, и ее корреляционная функция зависит только от разности аргументов. Следовательно,случайная стационарная функция.

Отметим что, положив в корреляционной функции, найдем дисперсию

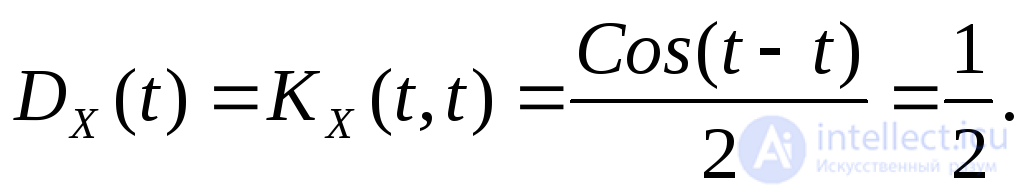
Таким образом, дисперсия сохраняет постоянное значение при всех значениях аргумента, как и должно, быть при случайной стационарной функции.

Большинство случайных стационарных процессов обладают важным для практики, так называемым, «эргодическим свойством», сущность которого состоит в том, что по одной, достаточно длинной отдельной реализации данного процесса можно судить обо всех свойствах процесса также как по любому количеству реализаций.

Другими словами, отдельные характеристики с.с.п. могут быть определены как соответствующие средние по времени для одной реализации достаточно большой продолжительности.

Связь между классами стационарных и случайных эргодических процессов можно охарактеризовать, например, как на рисунке 61.

Рис. 61 (Письм.).

Достаточным условием эргодического с.п. относительно математического ожидания и корреляционной функции является стремление к нулю его корреляционной функции при.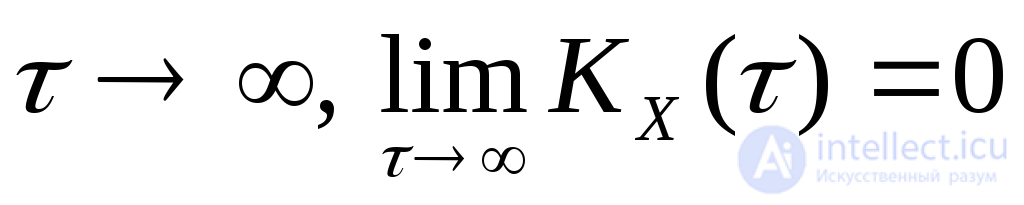

В качестве оценок характеристик эргодических с.с.п. принимают усредненное по времени значение:

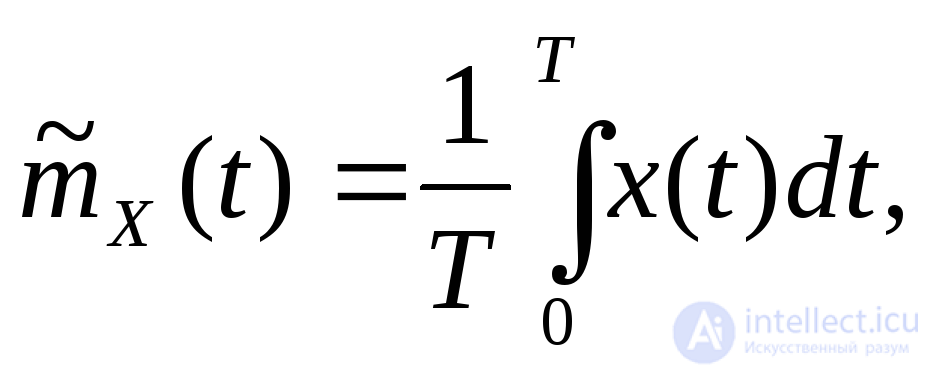
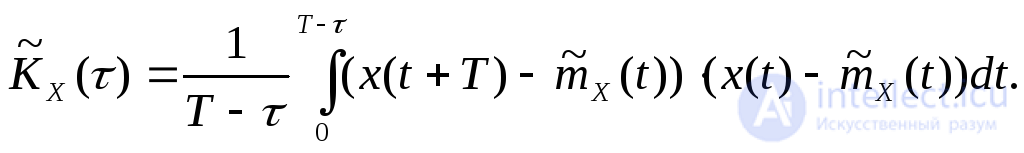
Интегралы, в правых частях равенств, на практике вычисляют приближенно.

Случайные процессы и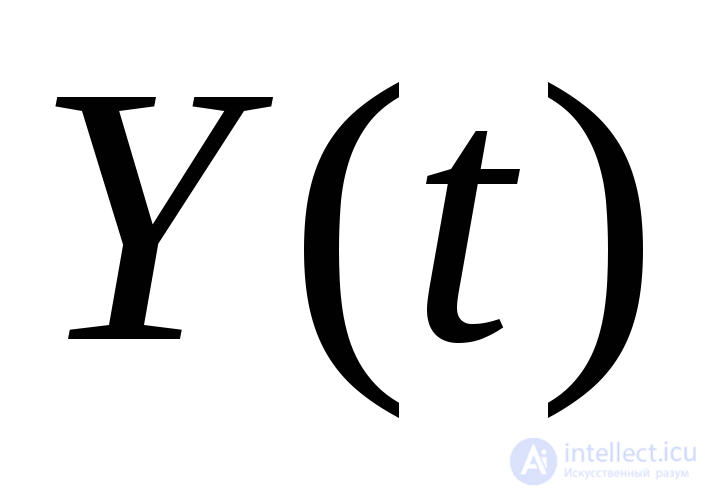называютсястационарно связанными, если их взаимно корреляционная функция 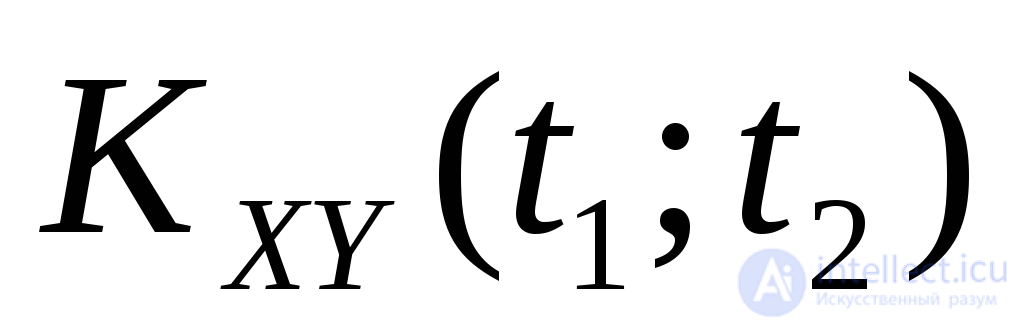зависит только от разности. В качестве примера стационарного процесса можно взять с.п.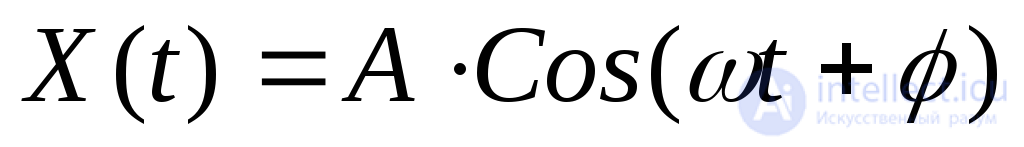– гармоническое колебание. Можно показать, что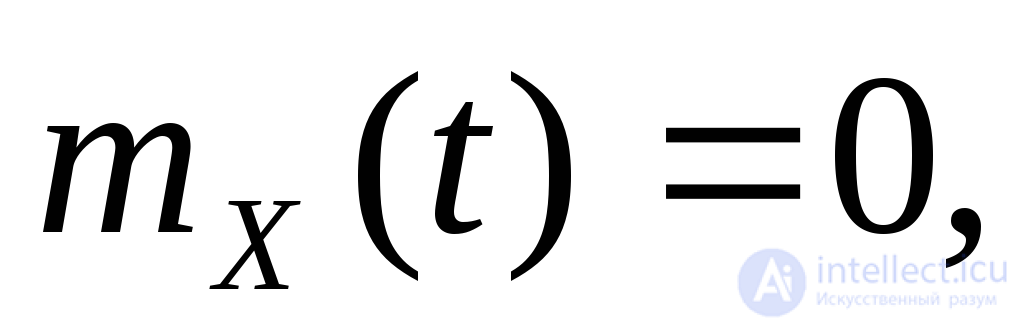а

Элементы спектральной теории стационарных

случайных процессов (функций)

В этом пункте кратко ознакомимся с новой характеристикой случайной функции, с понятием «спектральная плотность».

Из курса математического анализа известно, что неслучайную функцию 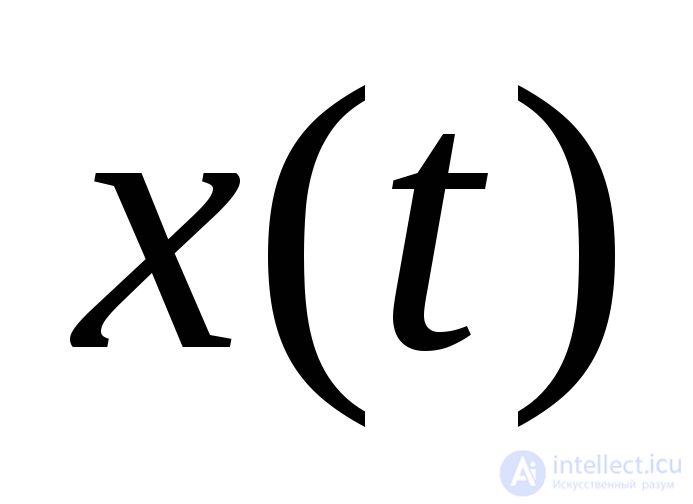, удовлетворяющую определенным условиям (условиям Дирихле) можно разложить в некотором промежуткев ряд Фурье. Важность теории рядов Фурье обусловлена той большой ролью, которую играют ее приложения не только в математике, но и в механике, физике и ряде других научных дисциплин. Во многом это предопределено тем, что тригонометрические ряды Фурье соединяют в себе особенности, как тригонометрических рядов, так и общих рядов Фурье. С теорией рядов Фурье и интегралах Фурье можно ознакомиться, например, в учебнике [Архипов, … ].

Аналогичную теорию можно применять и в теории случайных функций (процессов), т.е. любой с.п. 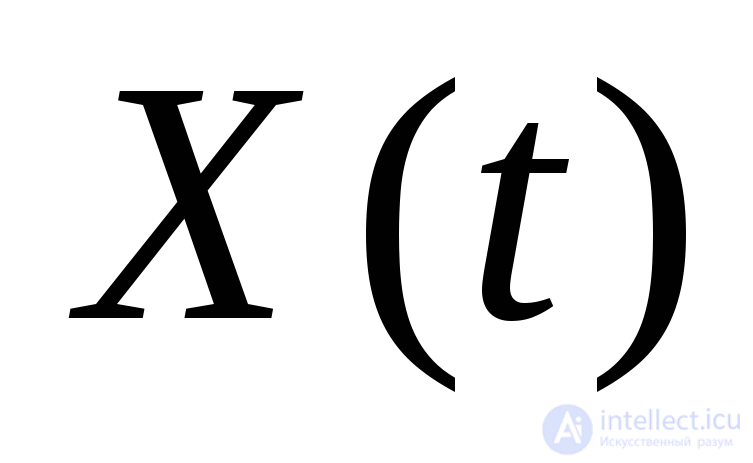можно представить (разложить) в виде суммы так называемых «элементарных случайных процессов». А именно, в функциональный ряд вида

(20)

где случайные величины,неслучайные функции времени. Метод разложения СП в ряды вида (20) упрощает различные преобразования СП (линейных и нелинейных), в частности используя ее можно найти характеристики «выходного процесса» стационарной линейной динамической системы по известным характеристикам «входного процесса». Вообще говоря, стационарную случайную функцию можно представить в виде гармонических колебаний со случайными амплитудами и случайными фазами. Рассмотрим два класса случайных функций:

А. Пусть случайная функция вида (локальный случай)

(21) ,

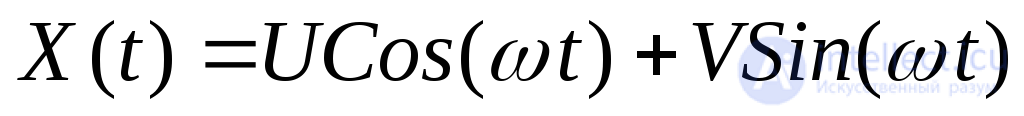гдедействительное число,инекоррелированные случайные величины с математическим ожиданием, равными нулю и одинаковыми дисперсиями, или коротко:

Напомним, что в наших условиях с.п. 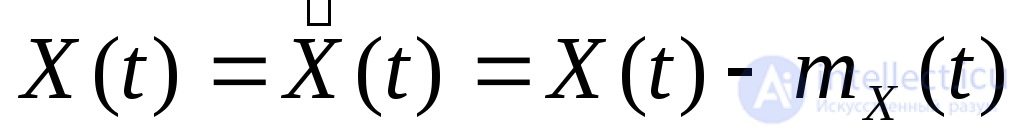, т.е.центрированный случайный процесс. Следовательно, такой случайный процесс является центрированным.

Покажем, что этот случайный процесс является стационарным.

Действительно, вычислим :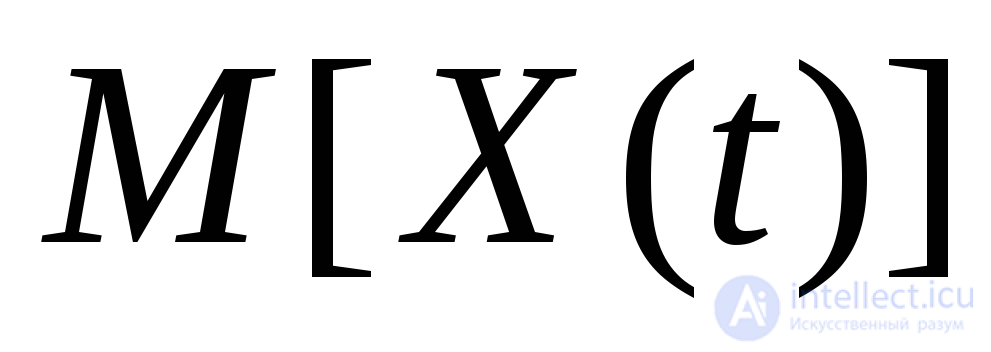

Вычислим корреляционную функцию. С учетом равенства:

,

и определения корреляционной функции имеем

Следовательно, мы доказали, чтоявляется стандартным случайным процессом.

Б. Рассмотрим теперь СП 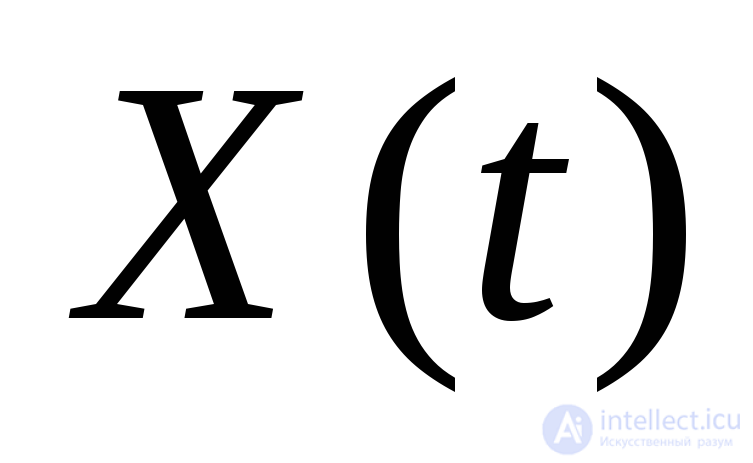, являющейся суммой бесконечного числа слагаемых вида (21) (общий случай)

(22),

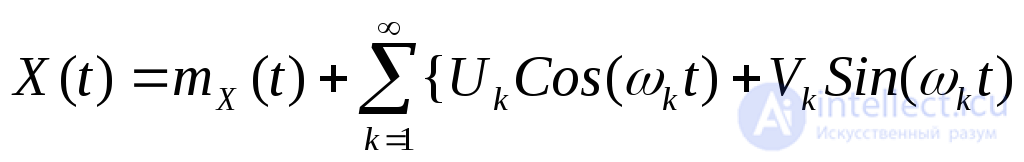где выполнены следующие условия:

(23)

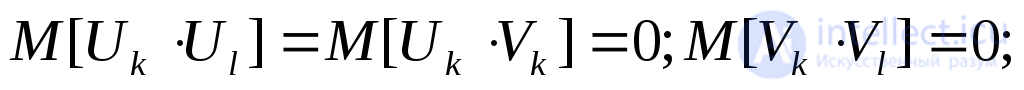
при любых 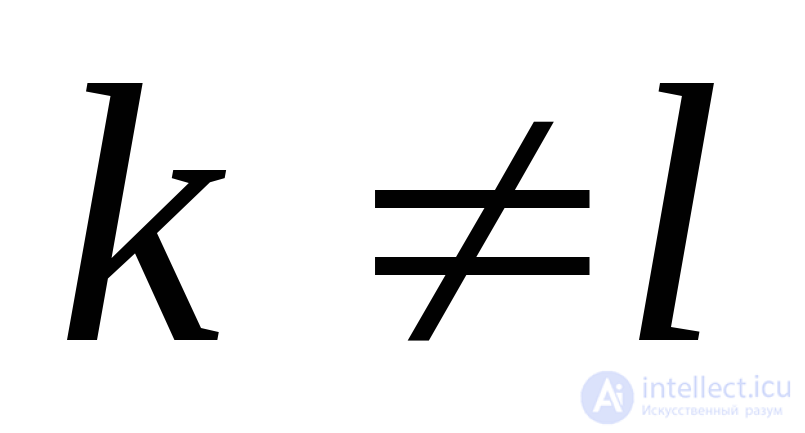,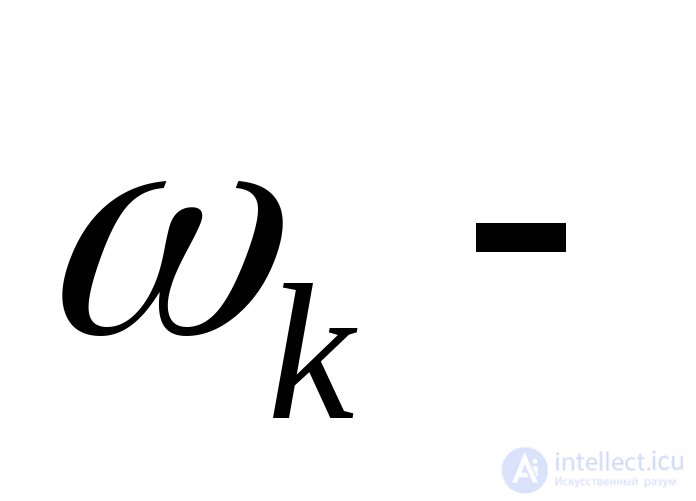постоянные числа.

Покажем, что случайный процесс , определенный равенством(22) с условиями (23) также является стационарным.

Действительно, с учетом свойства м.о. имеем

.

Следовательно, .

Поскольку слагаемые в равенстве (22) некоррелированные, то с учетом формулы для корреляционной функции с.п. (21) и свойства 6, пункта 16.5, т.е. с учетом равенства

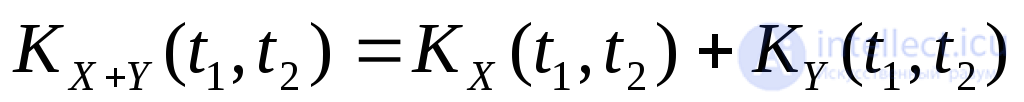
получаем

(24) ,

Итак, с.п. (23) является стационарным случайным процессом.

Отметим, что равенство (24) можно рассматривать как разложение корреляционной функции 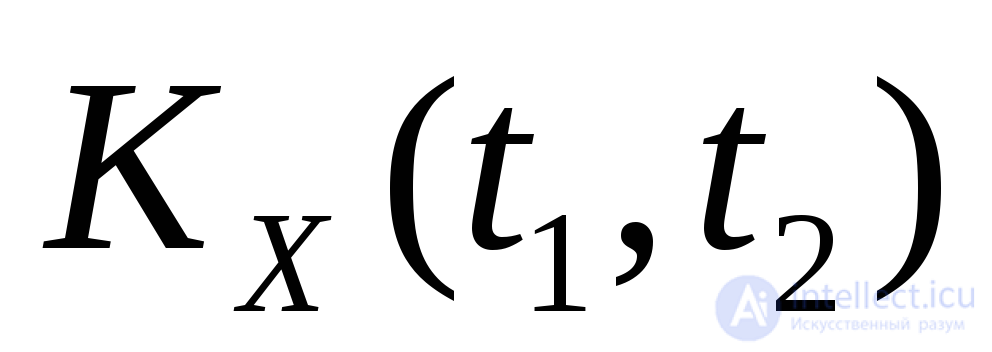на промежуткеи ряд Фурье по косинусам:,

где

,

(25)

Можно доказать, что 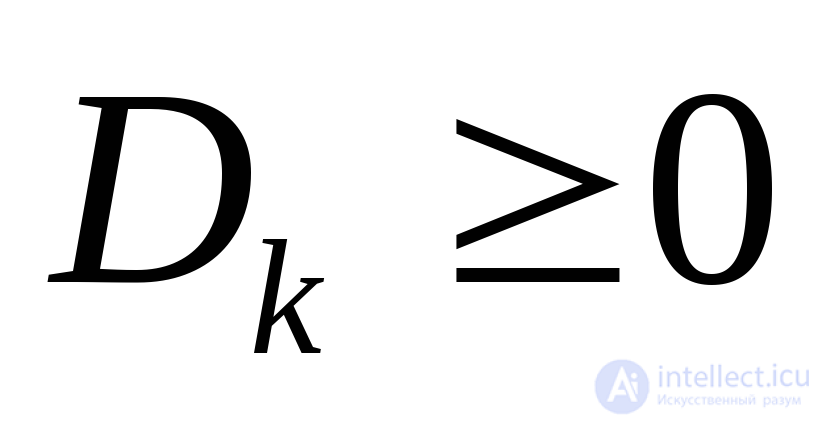для любой корреляционной функции стационарного случайного процесса.

Разложение (22) обычно называется каноническимилиспектральным разложением стационарного случайного процесса. А разложение (24) для которого выполнены равенства (25) называетсяспектральным разложением корреляционной функции СП с равноотстоящими частотами.

Отметим, что спектральное разложение (22) с.с.п. можно представить в виде суммы гармонических колебаний со случайными амплитудами и фазамии частотами:

(26) ,

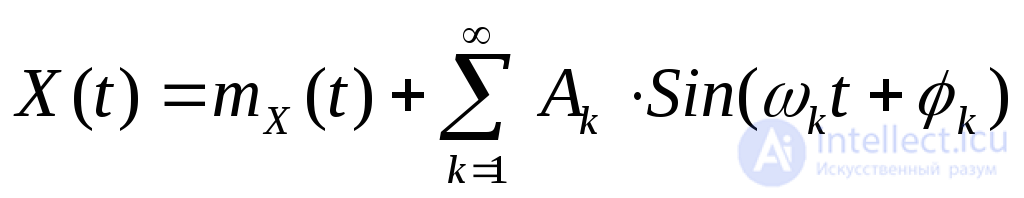где

Кратко наметим схему получения представление (26) на основании равенства (22), где 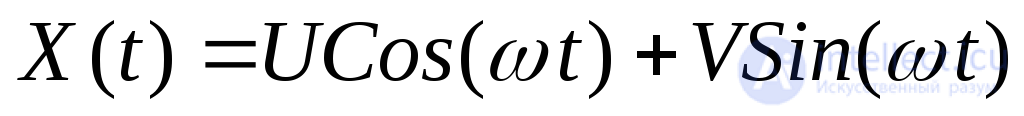и выполнены условий:

Очевидно, . Обозначим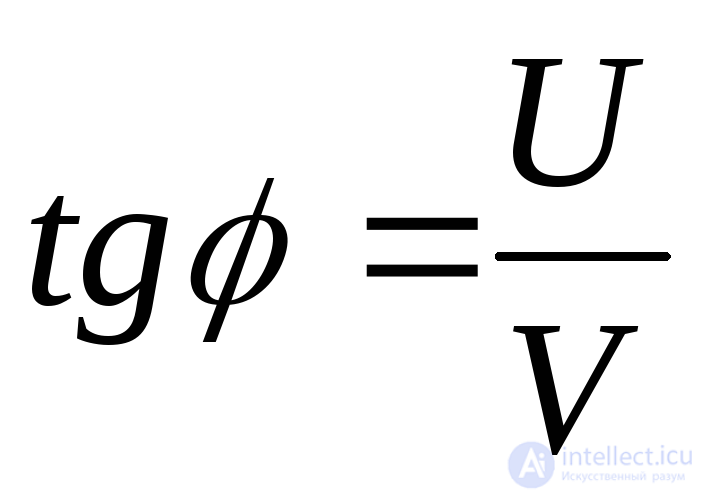и выполнив стандартные выкладки, получимгде

Отсюда вытекает, что каждую случайную функцию 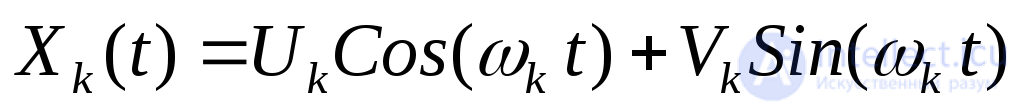в правой части (26) можно истолковать как гармоническое колебание со случайной амплитудой

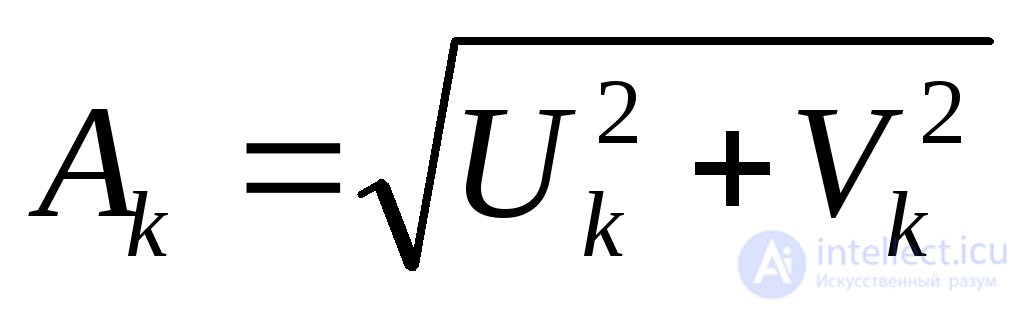+, частотой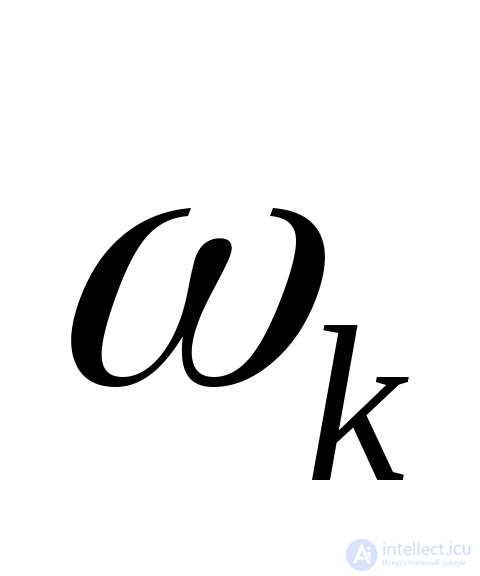ислучайной фазой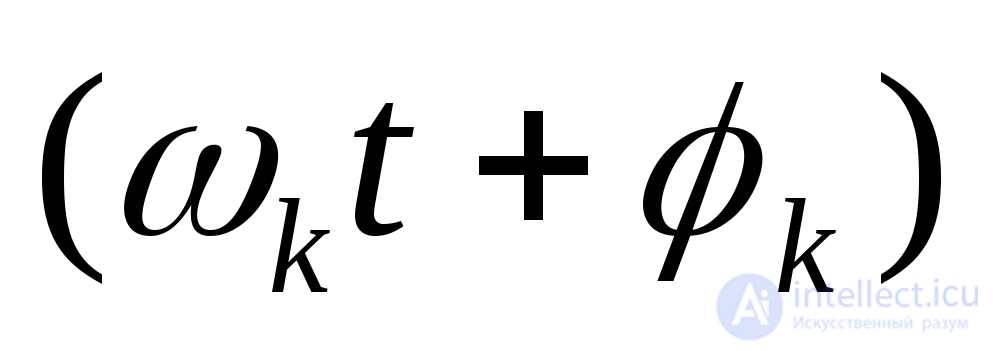. Отметим, что согласно условиям (23) величиныи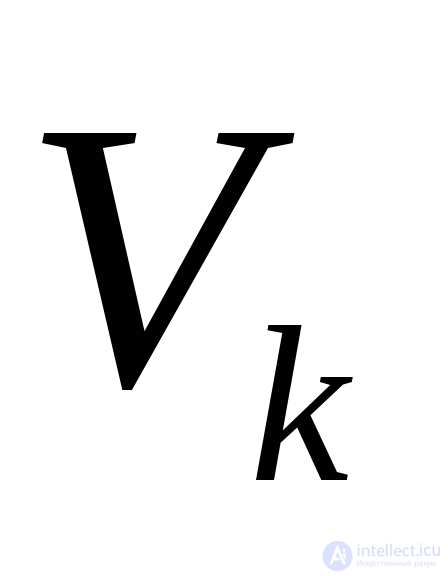будут центрированные случайные величины, т.е.

Я хотел бы услышать твое мнение про стационарные в широком смысле процессы Надеюсь, что теперь ты понял что такое стационарные в широком смысле процессы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы

Из статьи мы узнали кратко, но содержательно про стационарные в широком смысле процессы