Лекция
Привет, сегодня поговорим про цепь маркова, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое цепь маркова , настоятельно рекомендую прочитать все из категории вероятностные процессы.
Цепь Маркoва — последовательность случайных событий с конечным или счетным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова (старшего). цепь маркова – это распространенный и довольно простой способ моделирования случайных событий. Используется в самых разных областях, начиная генерацией текста и заканчивая финансовым моделированием

Пример цепи с двумя состояниями
Представьте, что существует только два погодных условия: может быть либо солнечно, либо пасмурно. Всегда можно безошибочно определить погоду в текущий момент. Гарантированно будет ясно или облачно.
Теперь вам захотелось научиться предсказывать погоду на завтрашний день. Интуитивно вы понимаете, что погода не может кардинально поменяться за один день. На это влияет множество факторов. Завтрашняя погода напрямую зависит от текущей и т. д. Таким образом, для того чтобы предсказывать погоду, вы на протяжении нескольких лет собираете данные и приходите к выводу, что после пасмурного дня вероятность солнечного равна 0,25. Логично предположить, что вероятность двух пасмурных дней подряд равна 0,75, так как мы имеем всего два возможных погодных условия.
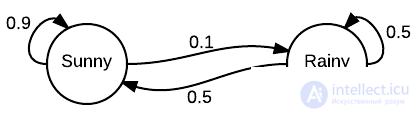
Теперь вы можете прогнозировать погоду на несколько дней вперед, основываясь на текущей погоде.
Этот пример показывает ключевые понятия цепи Маркова. Цепь Маркова состоит из набора переходов, которые определяются распределением вероятностей, которые в свою очередь удовлетворяют Марковскому свойству.
Обратите внимание, что в примере распределение вероятностей зависит только от переходов с текущего дня на следующий. Это уникальное свойство Марковского процесса – он делает это без использования памяти. Как правило, такой подход не способен создать последовательность, в которой бы наблюдалась какая-либо тенденция. Например, в то время как цепь Маркова способна сымитировать стиль письма, основанный на частоте использования какого-то слова, она не способна создать тексты с глубоким смыслом, так как она может работать только с большими текстами. Именно поэтому цепь Маркова не может производить контент, зависящий от контекста.
Формально, цепь Маркова – это вероятностный автомат. Распределение вероятностей переходов обычно представляется в виде матрицы. Если цепь Маркова имеет N возможных состояний, то матрица будет иметь вид N x N, в которой запись (I, J) будет являться вероятностью перехода из состояния I в состояние J. Кроме того, такая матрица должна быть стохастической, то есть строки или столбцы в сумме должны давать единицу. В такой матрице каждая строка будет иметь собственное распределение вероятностей.
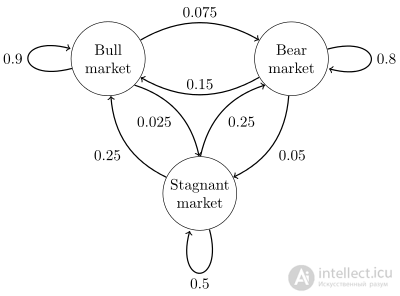
Общий вид цепи Маркова с состояниями в виде окружностей и ребрами в виде переходов.
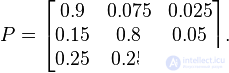
Примерная матрица перехода с тремя возможными состояниями.
Цепь Маркова имеет начальный вектор состояния, представленный в виде матрицы N x 1. Он описывает распределения вероятностей начала в каждом из N возможных состояний. Запись I описывает вероятность начала цепи в состоянии I.

Этих двух структур вполне хватит для представления цепи Маркова.
Мы уже обсудили, как получить вероятность перехода из одного состояния в другое, но что насчет получения этой вероятности за несколько шагов? Для этого нам необходимо определить вероятность перехода из состояния I в состояние J за M шагов. На самом деле это очень просто. Матрицу перехода P можно определить вычислением (I, J) с помощью возведения P в степень M. Для малых значений M это можно делать вручную, с помощью повторного умножения. Но для больших значений M, если вы знакомы с линейной алгеброй, более эффективным способом возведения матрицы в степень будет сначала диагонализировать эту матрицу.
Последовательность дискретных случайных величин 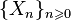 называется простой цепью Маркова (с дискретным временем), если
называется простой цепью Маркова (с дискретным временем), если
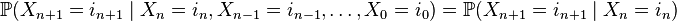 .
.
Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний (в отличие от цепей Маркова высших порядков).
Область значений случайных величин 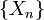 называется простра́нством состоя́ний цепи, а номер
называется простра́нством состоя́ний цепи, а номер 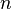 — номером шага.
— номером шага.
Матрица 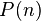 , где
, где
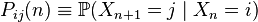
называется ма́трицей перехо́дных вероя́тностей на 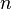 -м шаге, а вектор
-м шаге, а вектор 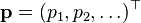 , где
, где

— нача́льным распределе́нием цепи Маркова.
Очевидно, матрица переходных вероятностей является стохастической, то есть
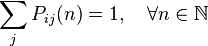 .
.
Цепь Маркова называется одноро́дной, если матрица переходных вероятностей не зависит от номера шага, то есть
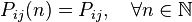 .
.
В противном случае цепь Маркова называется неоднородной. В дальнейшем будем предполагать, что имеем дело с однородными цепями Маркова.
Из свойств условной вероятности и определения однородной цепи Маркова получаем:
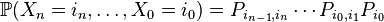 ,
,
откуда вытекает специальный случай уравнения Колмогорова — Чепмена:
 ,
,
то есть матрица переходных вероятностей за 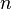 шагов однородной цепи Маркова есть
шагов однородной цепи Маркова есть 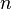 -я степень матрицы переходных вероятностей за 1 шаг. Наконец,
-я степень матрицы переходных вероятностей за 1 шаг. Наконец,
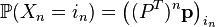 .
.
Семейство дискретных случайных величин  называется цепью Маркова (с непрерывным временем), если
называется цепью Маркова (с непрерывным временем), если
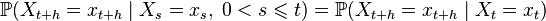 .
.
Цепь Маркова с непрерывным временем называется однородной, если
 .
.
Аналогично случаю дискретного времени, конечномерные распределения однородной цепи Маркова с непрерывным временем полностью определены начальным распределением

и ма́трицей перехо́дных фу́нкций (переходных вероятностей)
 .
.
Матрица переходных вероятностей удовлетворяет уравнению Колмогорова — Чепмена: 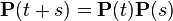 или
или
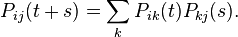
По определению, матрица интенсивностей 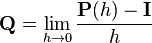 или, что эквивалентно,
или, что эквивалентно,
 .
.
Из уравнения Колмогорова — Чепмена следуют два уравнения:
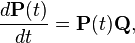
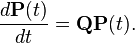
Для обоих уравнений начальным условием выбирается 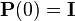 . Об этом говорит сайт https://intellect.icu . Соответствующее решение
. Об этом говорит сайт https://intellect.icu . Соответствующее решение 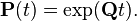
Для любого 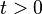 матрица
матрица 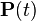 обладает следующими свойствами:
обладает следующими свойствами:
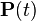 неотрицательны:
неотрицательны: 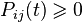 (неотрицательность вероятностей).
(неотрицательность вероятностей).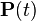 равна 1:
равна 1:  (полная вероятность), то есть матрица
(полная вероятность), то есть матрица 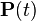 является стохастической справа (или по строкам).
является стохастической справа (или по строкам). матрицы
матрицы 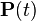 не превосходят 1 по абсолютной величине:
не превосходят 1 по абсолютной величине:  . Если
. Если 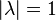 , то
, то 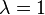 .
.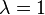 матрицы
матрицы 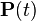 соответствует, как минимум, один неотрицательный левый собственный вектор-строка (равновесие):
соответствует, как минимум, один неотрицательный левый собственный вектор-строка (равновесие): 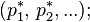

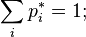
 .
.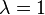 матрицы
матрицы 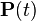 все корневые векторы являются собственными, то есть соответствующие жордановы клетки тривиальны.
все корневые векторы являются собственными, то есть соответствующие жордановы клетки тривиальны.Матрица 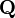 обладает следующими свойствами:
обладает следующими свойствами:
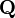 неотрицательны:
неотрицательны: 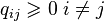 .
.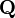 неположительны:
неположительны: 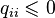 .
.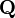 равна 0:
равна 0: 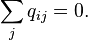
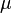 матрицы
матрицы 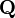 неположительна:
неположительна: 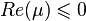 . Если
. Если 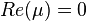 , то
, то 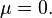
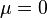 матрицы
матрицы 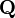 соответствует, как минимум, один неотрицательный левый собственный вектор-строка (равновесие):
соответствует, как минимум, один неотрицательный левый собственный вектор-строка (равновесие): 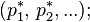

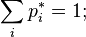
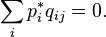
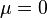 матрицы
матрицы 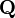 все корневые векторы являются собственными, то есть соответствующие жордановы клетки тривиальны.
все корневые векторы являются собственными, то есть соответствующие жордановы клетки тривиальны.Для цепи Маркова с непрерывным временем строится ориентированный граф переходов (кратко — граф переходов) по следующим правилам:
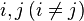 соединяются ориентированным ребром
соединяются ориентированным ребром 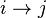 , если
, если 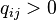 (то есть интенсивность потока из
(то есть интенсивность потока из 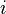 -го состояния в
-го состояния в 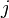 -е положительна.
-е положительна.Топологические свойства графа переходов связаны со спектральными свойствами матрицы 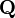 . В частности, для конечных цепей Маркова верны следующие теоремы:
. В частности, для конечных цепей Маркова верны следующие теоремы:
А. Для любых двух различных вершин графа переходов 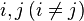 найдется такая вершина
найдется такая вершина 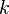 графа («общий сток»), что существуют ориентированные пути от вершины
графа («общий сток»), что существуют ориентированные пути от вершины 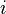 к вершине
к вершине 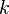 и от вершины
и от вершины 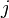 к вершине
к вершине 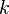 . Замечание: возможен случай
. Замечание: возможен случай 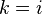 или
или 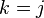 ; в этом случае тривиальный (пустой) путь от
; в этом случае тривиальный (пустой) путь от 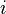 к
к 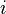 или от
или от 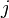 к
к 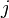 также считается ориентированным путем.
также считается ориентированным путем.
Б. Нулевое собственное число матрицы 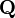 невырождено.
невырождено.
В. При  матрица
матрица 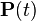 стремится к матрице, у которой все строки совпадают (и совпадают, очевидно, с равновесным распределением).
стремится к матрице, у которой все строки совпадают (и совпадают, очевидно, с равновесным распределением).
А. Граф переходов цепи ориентированно связен.
Б. Нулевое собственное число матрицы 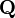 невырождено и ему соответствует строго положительный левый собственный вектор (равновесное распределение).
невырождено и ему соответствует строго положительный левый собственный вектор (равновесное распределение).
В. Для некоторого 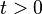 матрица
матрица 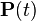 строго положительна (то есть
строго положительна (то есть 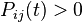 для всех
для всех 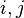 ).
).
Г. Для всех 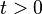 матрица
матрица 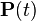 строго положительна.
строго положительна.
Д. При  матрица
матрица 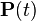 стремится к строго положительной матрице, у которой все строки совпадают (и совпадают, очевидно, с равновесным распределением).
стремится к строго положительной матрице, у которой все строки совпадают (и совпадают, очевидно, с равновесным распределением).

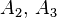 ); b) слабо эргодическая, но не эргодическая цепь (граф переходов не является ориентированно связным) c) эргодическая цепь (граф переходов ориентированно связен).
); b) слабо эргодическая, но не эргодическая цепь (граф переходов не является ориентированно связным) c) эргодическая цепь (граф переходов ориентированно связен).Рассмотрим цепи Маркова с тремя состояниями и с непрерывным временем, соответствующие графам переходов, представленным на рис. В случае (a) отличны от нуля только следующие недиагональные элементы матрицы интенсивностей — 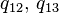 , в случае (b) отличны от нуля только
, в случае (b) отличны от нуля только 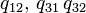 , а в случае (c) —
, а в случае (c) —  . Остальные элементы определяются свойствами матрицы
. Остальные элементы определяются свойствами матрицы 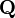 (сумма элементов в каждой строке равна 0). В результате для графов (a), (b), (c) матрицы интенсивностей имеют вид:
(сумма элементов в каждой строке равна 0). В результате для графов (a), (b), (c) матрицы интенсивностей имеют вид: 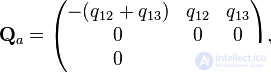
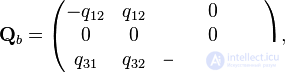

Основное кинетическое уравнение описывает эволюцию распределения вероятностей в цепи Маркова с непрерывным временем. «Основное уравнение» здесь — не эпитет, а перевод термина англ. Master equation. Для вектора-строки распределения вероятностей  основное кинетическое уравнение имеет вид:
основное кинетическое уравнение имеет вид:
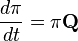
и совпадает, по существу, с прямым уравнением Колмогорова. В физической литературе чаще используют векторы-столбцы вероятностей и записывают основное кинетическое уравнение в виде, который явно использует закон сохранения полной вероятности:
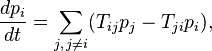
где 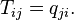
Если для основного кинетического уравнения существует положительное равновесие 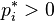 , то его можно записать в форме
, то его можно записать в форме
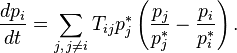
Для основного кинетического уравнения существует богатое семейство выпуклых функций Ляпунова — монотонно меняющихся со временем функций распределения вероятностей. Пусть 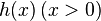 — выпуклая функция одного переменного. Для любого положительного распределения вероятностей (
— выпуклая функция одного переменного. Для любого положительного распределения вероятностей (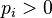 ) определимфункцию Моримото
) определимфункцию Моримото 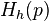 :
:
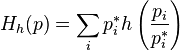 .
.
Производная 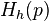 по времени, если
по времени, если 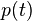 удовлетворяет основному кинетическому уравнению, есть
удовлетворяет основному кинетическому уравнению, есть
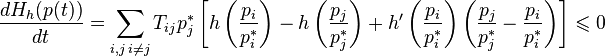 .
.
Последнее неравенство справедливо из-за выпуклости 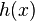 .
.
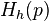 [править ]
[править ]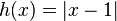 ,
, 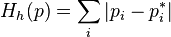 ;
;эта функция — расстояние от текущего распределения вероятностей до равновесного в  -норме. Сдвиг по времени является сжатием пространства вероятностных распределений в этой норме. (О свойствах сжатий см. статью Теорема Банаха о неподвижной точке.)
-норме. Сдвиг по времени является сжатием пространства вероятностных распределений в этой норме. (О свойствах сжатий см. статью Теорема Банаха о неподвижной точке.)
 ,
, 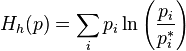 ;
;эта функция — (минус) энтропия Кульбака (см. Расстояние Кульбака — Лейблера). В физике она соответствует свободной энергии, деленной на 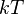 (где
(где 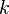 —постоянная Больцмана,
—постоянная Больцмана, 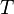 — абсолютная температура):
— абсолютная температура):
если 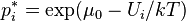 (распределение Больцмана), то
(распределение Больцмана), то
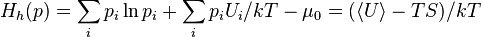 .
.
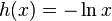 ,
, 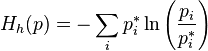 ;
;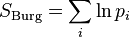
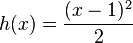 ,
, 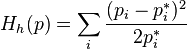 ;
;это квадратичное приближение для (минус) энтропии Кульбака вблизи точки равновесия. С точностью до постоянного во времени слагаемого эта функция совпадает с (минус) энтропией Фишера, которую дает следующий выбор,
 ,
, 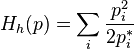 ;
;это (минус) энтропия Фишера.
 ,
, 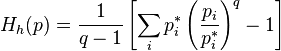 ;
;это один из аналогов свободной энергии для энтропии Тсаллиса. Энтропия Тсаллиса (Tsallis entropy)
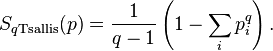
служит основой для статистической физики неэкстенсивных величин. При 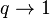 она стремится к классической энтропии Больцмана — Гиббса — Шеннона, а соответствующая функция Моримото — к (минус) энтропии Кульбака.
она стремится к классической энтропии Больцмана — Гиббса — Шеннона, а соответствующая функция Моримото — к (минус) энтропии Кульбака.
Одной из первых научных дисциплин, в которой цепи Маркова нашли практическое применение, стала лингвистика (в частности текстология). Сам Марков для иллюстрации своих результатов исследовал зависимость в чередовании гласных и согласных в первых главах «Евгения Онегина» и «Детских годов Багрова-внука» ].
Надеюсь, эта статья про цепь маркова, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое цепь маркова и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы