Лекция
Привет, Вы узнаете о том , что такое понятие клеточного автомата, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое понятие клеточного автомата, клеточный автомат , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
Понятие клеточного автомата не является новым. Оно описано во многих книгах [1, 9] и, более того, есть люди, которые посвятили клеточным
автоматам всю жизнь .
История клеточных автоматов начинается более полувека назад. Многие книги указывают, что клеточный автомат – это результат работы Джона фон
Немана (John von Neumann) и Конрада Цузе (Konrad Zuse), которые в начале сороковых годов 20 века разработали в идею универсальной вычислительной
среды для построения, анализа и сравнения характеристик алгоритмов [10]. Работы этих ученых базируются на исследованиях Станислава Улама
(Stanislaw Ulam) [11].
Клеточный автомат — дискретная модель, изучаемая в математике, теории вычислимости, физике, теоретической биологии и микромеханике. Включает регулярную решетку ячеек, каждая из которых может находиться в одном из конечного множества состояний, таких как 1 и 0. Решетка может быть любой размерности. Для каждой ячейки определено множество ячеек, называемых окрестностью. К примеру, окрестность может быть определена как все ячейки на расстоянии не более 2 от текущей (окрестность фон Неймана ранга 2). Для работы клеточного автомата требуется задание начального состояния всех ячеек и правил перехода ячеек из одного состояния в другое. На каждой итерации, используя правила перехода и состояния соседних ячеек, определяется новое состояние каждой ячейки. Обычно правила перехода одинаковы для всех ячеек и применяются сразу ко всей решетке.
Основное направление исследования клеточных автоматов — алгоритмическая разрешимость тех или иных задач. Также рассматриваются вопросы построения начальных состояний, при которых клеточный автомат будет решать заданную задачу.
На сегодняшний день клеточные автоматы нашли широкое распространение во всех сферах человеческой деятельности: математика, физика, биология [12], химия, механика, криптография [13], гидродинамика, газодинамика [14, 15] и т.д. Основным направлением применения клеточных
автоматов является моделирование динамических процессов, например, движение толпы [16] или распространение тепловых потоков [17]. Некоторые
ученые считают, что клеточные автоматы – это принцип, по которому сама природа действует в повседневной жизни. Наиболее подробно об этом
описано в книге Стивена Вольфрама (Stephen Wolfram) «A New Kind of Science» .
Принцип клеточных автоматов основан на локальных взаимодействиях. Все элементы в любой рассматриваемой системе действуют по одинаковым
принципам. В совокупности результаты работы простых правил, на которых основаны взаимодействия, позволяют получать сложное поведение. Джон
фон Нейман дает следующее определение клеточным автоматам: «Клеточные автоматы являются дискретными динамическими системами, поведение
которых полностью определяется в терминах локальных зависимостей. В значительной степени также обстоит дело для большого класса непрерывных
динамических систем, определенных уравнениями в частных производных. В этом смысле клеточные автоматы в информатике являются аналогом
физического понятия «поля»… клеточный автомат может мыслиться как стилизованный мир. Пространство представлено равномерной сеткой, каждая
ячейка или клетка которой содержит несколько битов данных; время идет вперед дискретными шагами, а законы мира выражаются единственным
набором правил, скажем, небольшой справочной таблицей, по которой любая клетка на каждом шаге вычисляет свое новое состояние по состояниям ее
близких соседей. Таким образом, законы системы являются локальными и повсюду одинаковыми. «Локальный» означает, что для того, чтобы узнать,
что произойдет здесь мгновение спустя, достаточно посмотреть на состояние ближайшего окружения: никакое дальнодействие не допускается.
«Одинаковость» означает, что законы везде одни и те же: я могу отличить одно место от другого только по форме ландшафта, а не по какой-то разнице
в законах» Формально клеточный автомат можно определить как набор {G, Z, N, f},
где G – метрика поля, на котором действует клеточный автомат;
Z – множество состояний каждой клетки;
N – окрестность клетки, которая влияет на состояние данной клетки;
f – правила клеточного автомата, которые в математическом виде могут быть записано Z x Z ^ |N| -> Z.
Свойствами клеточного автомата являются: локальность правил, однородность системы, конечность множества состояний клетки,
одновременность изменений для всех клеток. Более подробно и формально основные свойства классического клеточного автомата приведены в работе
[18].
Клеточные автоматы могут работать в нескольких измерениях: он может обрабатывать вектор состояний клеток, плоскость или трехмерную модель.
Во всех случаях для визуализации работы автомата часто добавляют дополнительное измерение – время, которое позволяет оценить изменения
состояний поля в динамике. Наиболее известным приложением клеточных автоматов можно считать игру «Жизнь» Джона Конвея (John Conway) [10, 19].
Существует несколько разновидностей клеточных автоматов. Ниже перечислены их основные типы из книги Стивена Вольфрама «A New Kind of
Science» .
Станислав Улам, работая в Лос-Аламосской национальной лаборатории в 1940-е годы, изучал рост кристаллов, используя простую решеточную модель . В это же время Джон фон Нейман, коллега Улама, работал над проблемой самовоспроизводящихся систем. Первоначальная концепция фон Неймана основывалась на идее робота, собирающего другого робота. Такая модель известна как кинематическая. Разработав эту модель, фон Нейман осознал сложность создания самовоспроизводящегося робота и, в частности, обеспечения необходимого «запаса частей», из которого должен строиться робот. Улам предложил фон Нейману использовать более абстрактную математическую модель, подобную той, что Улам использовал для изучения роста кристаллов. Таким образом возникла первая клеточно-автоматная система. Подобно решетке Улама, клеточный автомат фон Неймана двухмерный, а самовоспроизводящийся робот описан алгоритмически. Результатом явился универсальный конструктор, работающий «внутри» клеточного автомата с окрестностью, включающей непосредственно прилегающие ячейки, и имеющего 29 состояний. Фон Нейман доказал, что для такой модели существует паттерн, который будет бесконечно копировать самого себя.
Также в 1940-е годы, Норберт Винер и Артуро Розенблют (англ. Arturo Rosenblueth) разработали клеточно-автоматную модель возбудимой среды. Целью было математическое описание распространения импульса в сердечных нервных узлах. Их оригинальная работа продолжает цитироваться в современных исследованиях по аритмии и возбудимым средам.
В 1960-е годы клеточные автоматы изучались как частный тип динамических систем, и впервые была установлена их связь с областью символьной динамики. В 1969 году Г. А. Хедланд (англ. Gustav A. Hedlund) провел обзор результатов, полученных в этом направлении. Наиболее значимым результатом явилось описание набора правил клеточного автомата как множества непрерывных эндоморфизмов в сдвиговом пространстве.
В 1970-е получила известность двухмерная клеточно-автоматная модель с двумя состояниями, известная как игра «Жизнь». Изобретенная Джоном Конвеем и популяризованная Мартином Гарднером, она использует следующие правила: если клетка имеет двух «живых» соседей, она остается в прежнем состоянии. Если клетка имеет трех «живых» соседей, она переходит в «живое» состояние. В остальных случаях клетка «умирает». Несмотря на свою простоту, система проявляет огромное разнообразие поведения, колеблясь между очевидным хаосом и порядком. Одним из феноменов игры «Жизнь» являются глайдеры — сочетания клеток, движущиеся по сетке как единое целое. Возможно построить автомат, в котором глайдеры будут выполнять некоторые вычисления, и впоследствии было показано, что игра «Жизнь» может эмулировать универсальную машину Тьюринга.
В 1969 году немецкий инженер Конрад Цузе опубликовал книгу «Вычислимый космос», где выдвинул предположение, что физические законы дискретны по своей природе, и что вся Вселенная является гигантским клеточным автоматом. Это была первая книга из области, называемой сейчас цифровой физикой.
В 1983 Стивен Вольфрам опубликовал первую из серии статей, исследующих очень простой, но до сих пор неизученный класс клеточных автоматов, называемых элементарными клеточными автоматами. Неожиданная сложность поведения этих простых автоматов привела Вольфрама к предположению, что сложность естественных систем обусловлена сходным механизмом. Кроме того, в течение этого периода Вольфрам формулирует концепцию истинной случайности и вычислительной неприводимости, и выдвигает предположение, что Правило 110 может быть универсальным — факт, доказанный в 1990 году ассистентом Вольфрама Мэтью Куком.
В 1987 году Брайан Сильверман (англ. Brian Silverman) предложил клеточный автомат Wireworld.
В 2002 году Вольфрам публикует 1280-страничный текст «Наука нового типа» (A New Kind of Science), где широко аргументирует, что достижения в области клеточных автоматов не являются изолированными, но весьма устойчивы и имеют большое значение для всех областей науки.
11-го ноября 2002 года Пауль Чепмен (англ. Paul Chapman) построил образец Жизни, который является РММ (Регистровой Машиной Минского). Фактически РММ эквивалентна машине Тьюринга. Первая версия образца была большой (268’096 живых ячеек на площади 4,558 x 21,469 клеток) и медленной (20 поколений/сек при использовании Life32 Иогана Бонтеса (англ. Johan Bontes) на 400 MHz AMD K6-II). Таким образом, в игре Жизнь можно выполнить любой алгоритм, который можно реализовать на современном компьютере.
Двумерный клеточный автомат можно определить как множество конечных автоматов на плоскости, помеченных целочисленными координатами (i, j), каждый из которых может находиться в одном из состояний :
.
Изменение состояний автоматов происходит согласно правилу перехода
,
где — некоторая окрестность точки
. К примеру, окрестность фон Неймана определяется как
,
а окрестность Мура
.
Число всех возможных правил перехода определяется числом состояний и количеством соседей n и составляет

Правило 40 (Класс 1) со случайными начальными условиями. Как видно, информация быстро исчезает в этой системе.

Правило 3 (Класс 2) со случайными начальными условиями. Очевидно появление периодических структур

Правило 18 (Класс 3) со случайными начальными условиями. Видно, что начальные условия порождают хаотические движения внутри системы.

Правило 193 (Класс 4) со случайными начальными условиями. Можно увидеть порождение устойчивых структур (колонка белых треугольников) и взаимодействие таких структур в других частях изображения.
Стивен Вольфрам в своей книге A New Kind of Science предложил 4 класса, на которые все клеточные автоматы могут быть разделены в зависимости от типа их эволюции. Классификация Вольфрама была первой попыткой классифицировать сами правила, а не типы поведения правил по отдельности. В порядке возрастания сложности классы выглядят следующим образом:
Такого рода определения носят по большей части качественный характер и их можно по-разному интерпретировать. Вот что Вольфрам говорит об этом:
Практически при всякой попытке классификации будут возникать ситуации, когда по одному свойству предмет можно отнести к одному классу, а какому-либо другому свойству — к другому классу. Такая же ситуация и с клеточными автоматами: встречаются правила, которые показывают свойства, присущие одновременно одному и другому классу.
Оригинальный текст (англ.)
Существует специальный класс клеточных автоматов, называемых тоталистичными. На каждом шаге эволюции клеточного автомата значение ячейки равно какому-либо целому числу (обычно выбираемого из конечного множества), а новое состояние клетки определяется суммой значений клеток-соседей и, возможно, предыдущим состоянием клетки. Если состояние клетки на новом шаге зависит от ее предыдущего состояния, то такой клеточный автомат называется внешним тоталистичным. Игра Жизнь является примером внешнего тоталистического клеточного автомата с набором значений ячеек {\displaystyle {0,1}}.
Термин тоталистичный происходит от английского totalistic. В свою очеред total может быть переведено как сумма, что и отражено в принципе действия этого типа автоматов, когда новое значение клетки зависит от суммы значений других клеток.
Существует множество возможных обобщений концепций клеточных автоматов.
Клеточный автомат, работающий на сетке, компонентами которой являются шестиугольники, а не квадраты (правило 34/2)
Один из них — использование сетки не с квадратами (гиперкубами в многомерном случае), а с другими геометрическими фигурами в ее основе. Например, если поле представлено шестиугольным паркетом, то шестиугольники будут клетками. Однако иногда такие клеточные автоматы оказывались идентичными клеточным автоматам на сетке с квадратными клетками, только при этом было необходимо ввести специальные правила отношений с клетками-соседями. Другой способ обобщения — использование нерегулярной сетки(например, в виде Мозаики Пенроуза).
Еще один способ — использование вероятностных правил. Такие клеточные автоматы называются стохастическими. В таких системах задается вероятность, что на следующем шаге клетка сменит свой цвет на другой. Или, например, в игре «Жизнь» добавляется правило, что клетка с определенной вероятностью может изменить свой цвет на противоположный, а другие правила этого клеточного автомата остаются без изменений.
Определение соседства клетки может меняться с течением времени и/или пространства. Например, на первом шаге соседями будут горизонтально смежные клетки, а на другом — вертикально смежные.
В клеточных автоматах на новое состояние клетки не влияют новые состояния смежных клеток. Правило можно поменять: можно сделать так, что, например, в блоках 2 на 2 состояния клеток зависят от состояния клеток внутри блока и от таких-же смежных блоков.
Существуют непрерывные клеточные автоматы. В таких системах вместо дискретного набора состояний используются непрерывные функции (обычно определяемые на промежутке ).
Клеточный автомат называется обратимым, если для каждой текущей конфигурации существует только одна предшествующая конфигурация. Если рассматривать клеточный автомат как функцию, отображающую одну конфигурацию в другую, то обратимость предполагает биективность этой функции. Если клеточный автомат обратим, то его обратная эволюция также может быть описана клеточным автоматом. Конфигурации, не имеющие предшествующих, то есть недостижимые в данном клеточном автомате, носят название «Сады Эдема».
Для одномерных клеточных автоматов существуют алгоритмы определения обратимости или необратимости. Однако для клеточных автоматов с двумя и более измерениями таких алгоритмов нет.
Обратимые клеточные автоматы часто используют для моделирования таких физических феноменов, как динамика жидкости и газа, поскольку они подчиняются законам термодинамики. Такие автоматы специально создаются обратимыми. Такие системы изучались Томасо Тоффоли (Tommaso Toffoli) и Норманом Марголусом (Norman Margolus). Существует несколько типов обратимых конечных автоматов. Наиболее известными являются клеточный автомат второго порядка и блочный клеточный автомат. Обе эти модели следуют несколько модифицированному варианту определения клеточного автомата, однако доказано, что они могут быть эмулированы традиционным клеточным автоматом со значительно большим размером окрестности и числом состояний. Также, было доказано, что любой обратимый клеточный автомат может быть сэмулирован блочным клеточным автоматом.
Стандартные клеточные автоматы на основе классического определения.
Клетки поля такого автомата изменяют состояние в зависимости от
состояний соседних клеток, и, таким образом, поле изменяет свое состояние.
Примеры стандартных одномерных клеточных автоматов представлены на
рис. 1.
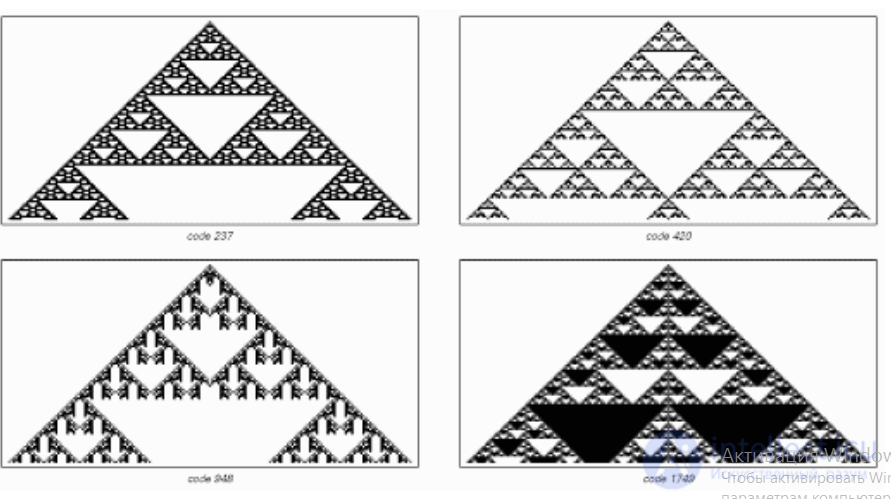
Рис. 1. Клеточные структуры, созданные с помощью стандартных клеточных автоматов
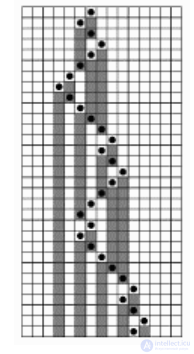
Рис. 2. Клеточная структура, созданная с помощью мобильного клеточного автомата
Мобильные клеточные автоматы подобно стандартным клеточным автоматам имеют состояния клеток, которые изменяются с течением времени, но в отличие от них дополнительно определена одна активная клетка. Только активная клетка изменяет состояние в каждый момент времени. Пример клеточной структуры, порожденной мобильным клеточным автоматом, изображен на рис. 2
Тьюринговые машины наподобие мобильного клеточного автомата имеет только одну активную клетку. Дополнительное условие – определение
нескольких состояний у активной клетки, как показано на рис. 3.
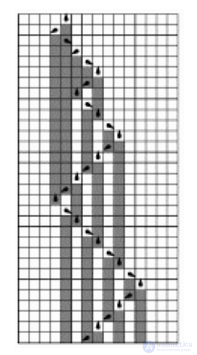
Рис. 3. Клеточная структура, созданная с помощью клеточного автомата – тьюринговой машины
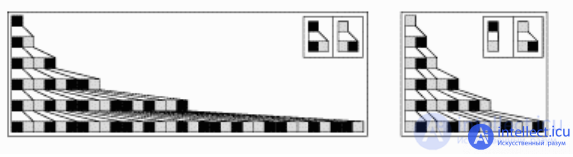
Рис. 4. Клеточная структура, созданная с помощью системы подстановок
Система подстановок – это клеточный автомат, который на каждом шаге заменяет клетку блоком из других клеток. Пример автомата показан на рис. 4
Последовательные подстановочные системы сканируют последовательность точек на соответствие условиям каждого правила, при удовлетворении правила происходит подстановка и сканирование начинается заново, как изображено на рис. 5
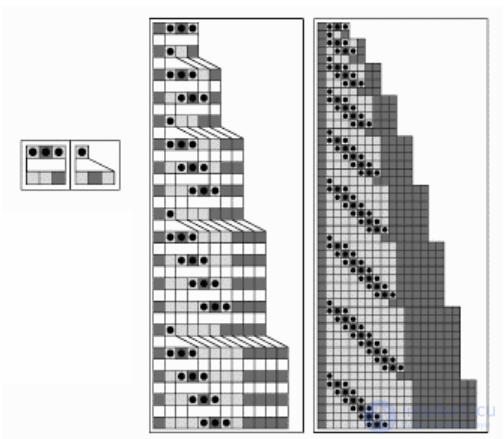
Рис. 5
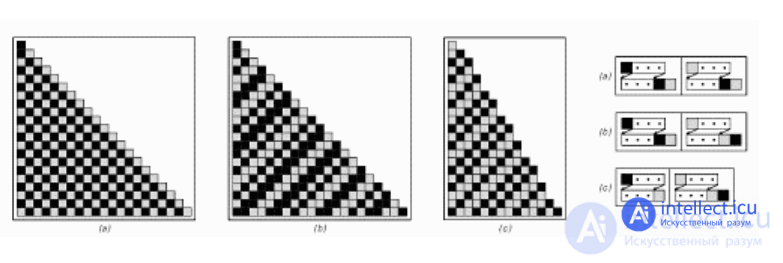
Рис. 6. Клеточная структура, созданная с помощью системы тэгов
Правила, которые удаляют элементы из начала цепочки клеток и добавляют другие клетки в конец цепочек, называются системами тэгов. Пример представлен на рис. 6.
Цикличность системы тэгов может достигаться за счет поочередного использования разных систем правил. В результате характер поведения клеточного автомата становится специфическим, что видно на рис. 7
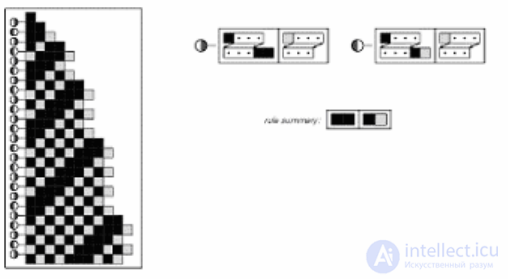
Рис. 7. Структура, созданная с помощью цикличной системы тэгов
Рис. Об этом говорит сайт https://intellect.icu . 8. Структура, созданная с помощью регистровой машины
Регистровые машины выполняют заданную программу. При успешном выполнении элемента программы происходит заданный переход, иначе
переход на следующий элемент. Пример приведен на рис. 8.
В символьной системе на каждом шаге каждый регион, заключенный в скобки, трансформируется по заданным правилам. В результате этого формируется последовательность. Пример показан на рис. 9

Рис. 9. Структура, созданная с помощью символьной системы
Понятие клеточного автомата с метками введено автором данной работы. Причиной его создания являлась необходимость достижения
заданных характеристик клеточных автоматов при разработке алгоритмов процесса распознавания текста. Как будет показано далее, это понятие
позволяет эффективно реализовать алгоритмы выделения признаков символов.
В процессе работы над дисертацией – анализа литературы – обнаружено понятие памяти в теории тьюринговых машин [20]. Оно определяет, что
головка тьюринговой машины может хранить некоторое конечное число данных, которые используются правилами автомата машины для изменения
ленты машины или передвижения ее головки. Данное понятие при введении некоторых ограничений и перехода на теорию клеточных автоматов может
быть также сведено к клеточным автоматам с метками. Принцип клеточной системы с метками заключается в ассоциации
каждой клетки поля с одним или несколькими метками.
Примером клеточного автомата с метками может служить набор: поле, на котором определены только клетки черного и белого цветов, метка,
которая может присутствовать или отсутствовать в клетках поля, и правила, учитывающие наличие меток у соседних клеток. В случае определения одной
метки для клеточного автомата, количество состояний каждой клетки увеличивается в два раза относительно случая без меток. В приведенном
примере количество состояний каждой клетки равно четырем. Правило клеточного автомата в такой системе будут выглядеть так, как представлено
на рис. 10.
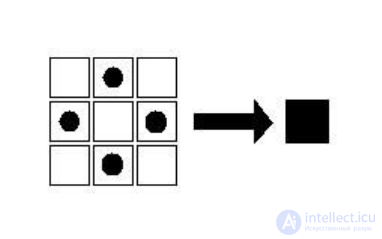
Рис. 10. Пример правила клеточного автомата с метками
В данном примере используется правило, основанное на восьми соседях. Без меток количество вариантов подобных правил (в случае определения
только двух цветов клеток) будет 2^10= 1024 (девять клеток условий и одна - результата). Добавляя метку, получится (2 · 2)^10= 1024^2= 1 048 576
вариантов правил. Удобнее, в данном случае, разделять двоеточием нумерацию цветов и меток. Тогда для правила, представленного на рисунке
10, номером может служить 1:340 (или в двоичном виде 0000000001:0101010100, где каждая цифра определяет состояние клетки,
клетки нумеруются слева направо сверху вниз), где первое число определяет правило преобразования цвета, а второе число – правило изменения метки.
Правило для поля, на котором определено более одной метки, нумеруется аналогичным образом: для правила с двумя метками – x : y : z,
где первое число определяет правило преобразования цвета, второе число – преобразование одной метки, третье число – второй метки.
Клеточный автомат с метками позволяет получать сложные результаты без изменения структуры исспользуемой системы клеток. Например, для
заданного изображения, данный автомат позволяет определить некоторые свойства данного изображения и выделить его характерные признаки без
изменения цвета.
Формальное описание
Клеточный автомат с метками – это набор {G, M, Z, N, f}. Описание каждого элемента представлено ниже.
1. G – конечное дискретное метрическое множество, гарантирующее конечность расстояний между клетками.
2. M – конечное множество меток, определенное для каждой клетки.
3. Z – конечный набор состояний клеток.
4. N – конечное множество, определяющее окрестность клетки таким образом, что каждый элемент множества позволяет определить соседа для
каждой клетки. |N| – количество соседних клеток, которые влияют на состояние данной.
5. f – правила клеточного автомата, соответствующие математической функции переходов:

Ниже показано, что клеточный автомат с метками удовлетворяет требованиям классического клеточного автомата.
По определению клеточный автомат задается четырьмя элементами {G*, Z*, N*, f*} [18]. Элементы G и N клеточного автомата с метками
соответствуют классическим элементам G* и N*.
Введем Z^ = Z x C таким образом, что |Z^| = |Z| x |C|. Множество Z^ будет соответствовать Z* классического определения клеточного автомата,
так как оно является конечным и определяет все варианты состояний клетки автомата.
Аналогично, f^ = (Z^ x Z^ )^ |N| -> Z^ будет соответствовать f*, так как учитываются все состояния на первом и втором временном слое.
Таким образом, получен набор {G, Z^, N, f^} клеточного автомата, в котором выполняются все свойства: локальность правил (обеспеченное N),
однородность системы на основе метрики G, конечность множества
состояний клетки Z^, одновременность изменений для всех клеток,гарантируемое набором правил f^.
Рассмотрм пример клеточного автомата с метками «шахматная доска». Задача автомата «шахматная доска» заключается в отрисовке
чередующихся черно-белых точек на белом изображении. Для выполнения задачи клеточному автомату с метками «шахматная
доска» достаточно восьми правил: 0:257, 0:65, 0:321, 1:52, 513:52, 256:52, 64:52, 320:52 (нерассмотренные состояния девяти исходных клеток не
изменяют состояние результирующей клетки). Эти правила изображены на рис. 11
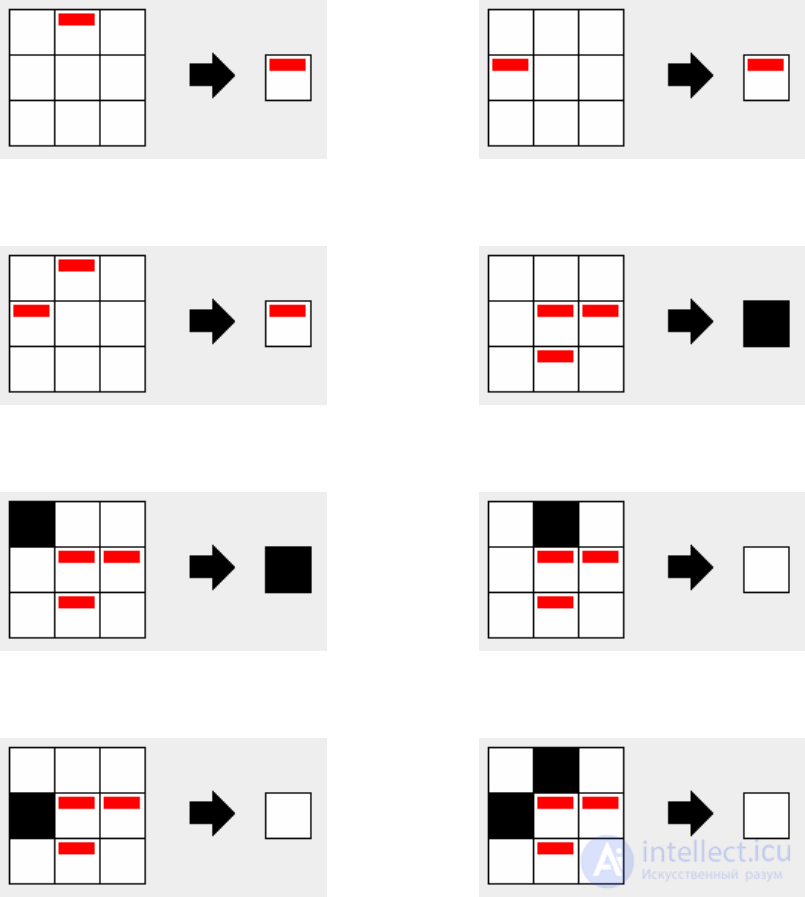
Рис. 11. Правила клеточного автомата «шахматная доска», правила:
а – 0:257, б – 0:65, в – 0:321, г – 1:52, д – 513:52, е - 256:52, ж – 64:52, з – 320:52
Для начала работы автомата необходимо поставить метку на стартовой точке поля. Результат работы автомата на шагах 1, 3, 5, 10, 20 изображены на
рис. 12.

Рис. 12. Результат работы клеточного автомата с метками «шахматная доска» на шагах
: а – первом, б – третьем, в – пятом, г – десятом, д – двадцатом
Данный пример иллюстрирует применение клеточных автоматов с метками, но не затрагивает практическую полезность, которую можно обеспечить с их использованием: возможность определения характеристик, не изменяя цвета обрабатываемого изображения.
Клеточный автомат – это мощный инструмент по выполнению задач моделирования. Четко определив все его составляющие (метрику поля,
состояния клеток, количество влияющих на клетку соседей и правила работы автомата), можно решить огромное число задач, многие из которых имеют не
тривиальные решения .
К сожалению, не все задачи, решение которых возможно на основе клеточных автоматов, могут быть решены с помощью их небольшого числа.
Более того, для решения части задач может потребоваться последовательность из клеточных автоматов, каждый из которых решает
специализированную задачу.
Последовательность клеточных автоматов – это совокупность клеточных автоматов, каждый из которых основан на специфических правилах.
Клеточные автоматы в последовательности запускаскаются в заданной последовательности и каждый очередной клеточный автомат начинает
работу на поле, который был сформирован предыдущим клеточным автоматом в последовательности.
Последовательность автоматов не обязательно будет усложнять логику работы системы. В разд. 3.2 будет показано, что использование
последовательности клеточных автоматов помогает обходиться небольшим числом правил для каждого клеточного автомата при решении
нетривиальной задачи
В случае использования клеточных автоматов с метками в последовательности клеточных автоматов необходимо заранее определить
одинаковый набор M возможных меток клеток поля каждого автомата. Это поможет поддерживать последовательность в работоспособном состоянии.
Простейшим нетривиальным клеточным автоматом будет одномерный клеточный автомат с двумя возможными состояниями, а соседями клетки будут смежные с ней клетки. Такие автоматы называются элементарными. Три клетки (центральная, ее соседи) порождают комбинаций состояний этих трех клеток. Далее на основе анализа текущего состояния тройки принимается решение о том, будет ли центральная клетка белой или черной на следующем шаге. Всего существует
возможных правил. Эти 256 правил кодируются в соответствии с кодом Вольфрама — стандартному соглашению, правилу, которое было предложено Вольфрамом. В некоторых статьях эти 256 правил были исследованы и сравнены. Наиболее интересными представляются правила с номерами 30 и 110. На двух изображениях ниже представлены эволюции указанных правил. Начальное условие для каждого автомата — одна центральная клетка — черная, остальные — белые. По оси
откладывается дискретное время, а по оси
откладываются состояния клеток автомата.

Правило 30
Правило 30
| Текущее состояние | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| Новое состояние центральной клетки | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |

Правило 110
Правило 110
| Текущее состояние | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| Новое состояние центральной клетки | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
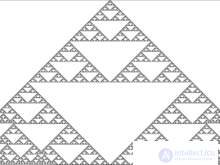
Правило 161
Правило 161
| Текущее состояние | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| Новое состояние центральной клетки | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Правило 30 проявляет поведение класса 3, что означает, что эволюция простых начальных условий приводит к хаотической, кажущейся случайной динамике.
Правило 110, как и игра «Жизнь» проявляет поведение класса 4, которое не является полностью случайным, но при этом отсутствует периодичность. При этом возникают структуры, которые взаимодействуют друг с другом неочевидным, сложным образом. Во время написания книги A New Kind of Science ассистент Стивена Вольфрама Мэттью Кук в 1994 году доказал, что некоторые из порождаемых правилом структур достаточно разнообразны, чтобы обладать полнотой по Тьюрингу. Этот факт представляет собой интерес, потому что в своей сути Правило 110 является простой одномерной системой. Также это хороший аргумент в пользу того, что системы класса 4 являются в некотором смысле универсальными. Мэттью Кук представил свое доказательство на конференции Института Санта-Фе в 1998 году, но Вольфрам запретил включать это доказательство в бумажную версию материалов конференции, потому что не хотел, чтобы оно было опубликовано до издания книги A New Kind of Science. В 2004 году доказательство Кука было опубликовано в журнале Вольфрама «Complex Systems»(выпуск 15, том 1), через 10 лет после того как Кук впервые представил его. Правило 110 было основой для построения наименьших Тьюринг-машин.
Правило 161 порождает фрактальные структуры, которые можно увидеть на рисунке. Можно видеть вложенные подобные треугольники.
Простейший одномерный клеточный автомат задается с помощью восьми бит. Таким образом, все правила клеточного автомата располагаются на вершинах 8-мерного единичного куба. Такой гиперкуб является пространством всех возможных одномерных клеточных автоматов. Для одномерного клеточного автомата, где соседями одной клетки являются соседи ее соседей необходимо бита и пространством всех возможных правил будет 32-мерный единичный куб. Расстоянием между двумя клеточными автоматами может считаться количество шагов, необходимых для того, чтобы перейти от одного правила к другому по ребрам многомерного куба. Такое расстояние называется расстоянием Хэмминга.
Исследования пространства правил клеточных автоматов позволяет ответить нам на вопрос, который ставится следующим образом: близко ли расположены относительно друг друга правила, которые порождают похожие друг на друга(в плане динамики) клеточные автоматы. Графическое представление гиперкуба высокой размерности на двумерной плоскости — весьма сложная задача. Однако на двумерной плоскости можно легко представить процесс эволюции одномерного клеточного автомата. При этом по одной оси откладывается дискретное время, а по другой — соответствующие состояния клеточного автомата. В случае двумерного клеточного автомата можно добавить третью ось. При этом две оси будут соответствовать состояниям клеточного автомата, а третья — дискретному времени. Процесс эволюции такого автомата представляет собой некоторую трехмерную фигуру в пространстве. Подробнее такие эксперименты описаны в книге Стивена Вольфрама A New Kind of Science. Исследования показали, что клеточные автоматы, классифицированные как класс 1, имели меньшее количество единичных бит в строке правила и они были сконцентрированы примерно в одном месте на гиперкубе. В то же время правила класса 3 имели большее (порядка 50 %) количество единичных бит.
Для пространств правил клеточных автоматов большей размерности было показано, что правила класса 4 расположены между классами 1 и 3.
Это наблюдение приводит к понятию грани хаоса применительно к теории клеточных автоматов и напоминает понятие фазового перехода в термодинамике.
Узор на поверхности раковины Conus textile формируется по механизму клеточного автомата
Некоторые живые организмы проявляют свойства клеточных автоматов. Раскраска раковин ряда морских моллюсков, например, родов Conus или Cymbiola, генерируется естественным одномерным клеточным автоматом, результат эволюции которого похож на Правило 30. Их пигментные клетки располагаются тонкой полоской вдоль края раковины. Секреция пигмента каждой клетки зависит от активирующей и ингибиторной активности соседних клеток. В процессе роста раковины полоса клеток формирует цветной узор на ее поверхности. Окраска чешуек ящерицы Timon lepidus описывается стохастическим клеточным автоматом .
Растения регулируют приток и отток газообразных веществ посредством механизма клеточных автоматов. Каждое устьице на поверхности листа действует подобно ячейке клеточного автомата .
Нейронные сети также могут быть использованы как клеточные автоматы. Сложный движущийся узор на коже головоногих является отражением паттернов активирования в мозгу животных.


Компьютерное моделирование реакции Белоусова — Жаботинского в тонком слое жидкости в чашке Петри.
Реакция Белоусова — Жаботинского представляет собой пространственно-временной химический осциллятор, который может быть смоделирован клеточным автоматом. В 1950-х годах А. М. Жаботинский, продолжая работу Б. П. Белоусова, обнаружил, что тонкий однородный слой смеси определенных химических веществ способен образовывать движущиеся геометрические узоры, такие как концентрические круги и спирали.
Клеточные автоматы также используются в моделировании экосистем и популяционной динамики .
Процессоры на клеточных автоматах — физическая реализация идей клеточного автомата. Элементы процессора размещены на равномерной сетке одинаковых ячеек. Состояние ячеек определяются взаимодействием со смежными клетками-соседями. В свою очередь соседство может определяться по фон Нейману или по Муру. Один из таких процессоров имеет вид систолической матрицы. Взаимодействие частиц может быть реализовано с помощью электрического тока, магнетизма, вибрации(например, фононы), либо и использованием любого другого способа передачи информации. Передача информации может быть осуществлена несколькими способами, которые не предусматривают использования проводников для передачи информации между элементами. Такой способ устройства процессора очень отличается от большинства процессоров, используемых на сегодняшний день и построенных по принципу фон Неймана, в которых процессор разделен на несколько секций, которые могут взаимодействовать между собой с использованием непосредственно проводников.
Правило 30 было предложено в качестве возможного блочного шифра для использования в криптографии. Двумерные клеточные автоматы используются для генерации случайных чисел. Клеточные автоматы предложены для использования в криптосистемах с открытым ключом. В этом случае односторонняя функция является результатом эволюции конечного клеточного автомата, первоначальное состояние которого сложно найти. По заданному правилу легко найти результат эволюции клеточного автомата, но очень сложно вычислить его предыдущие состояния.
Клеточные автоматы используются в компьютерном моделировании процессов рекристаллизации .
Как указывает Andrew Ilachinski в своей книге Клеточные автоматы (оригинальное название — Cellular Automata), многие исследователи задавались вопросом является ли наша вселенная клеточным автоматом. Andrew Ilachinski указывает, что смысл этого вопроса может быть понят лучше с помощью простого наблюдения, которое можно произвести следующим образом. Рассмотрим эволюцию Правила 110: если бы это было что-то вроде «инопланетной физики» (оригинал — alien physics), то как можно было бы описать возникающие закономерности? Если бы вы не знали, как получены конечное изображение эволюции автомата, вы могли бы предположить, что данный рисунок отражает некоторым образом движение каких-либо частиц. Тогда делается следующее предположение: возможно, наш мир, хорошо описываемый физикой элементарных частиц, может быть клеточным автоматом на фундаментальном уровне.
Однако, законченная теория, базирующаяся на этих утверждениях все еще далека от того, чтобы считаться законченной (равно как и сколько-нибудь общепринятой). Увлекаясь и развивая эту гипотезу, исследователи приходят к интересным заключениям, как можно использовать эту теорию для описания мира вокруг. Марвин Минский, пионер ИИ, разработал способ для изучения взаимодействия частиц с помощью четырехмерного клеточного автомата. Конрад Цузе, известный как создатель первого действительно работающего программируемого компьютера Z3 занимался клеточным автоматами на нерегулярных решетках для исследования вопроса информационного содержания частиц. Эдвард Фредкин представил то, что он называет «гипотезой конечной вселенной» (оригинал — finite nature hypothesis). Смысл гипотезы заключается в том, что
…всякая величина в физике, включая время и пространство, является конечной и дискретной.
Оригинальный текст
Фредкин и Вольфрам — последовательные приверженцы цифровой физики.
Герард ’т Хоофт разработал теорию квантовой физики, основывающуюся на клеточных автоматах[7
|
Игра «Жизнь» Конвея и другие клеточные автоматы |
|||||
|---|---|---|---|---|---|
| Классы конфигураций |
|
||||
| Конфигурации |
|
||||
|
|||||
| Другие КА на двумерной решетке |
|
||||
| Одномерные КА |
|
||||
| ПО и алгоритмы |
|
||||
| Исследователи КА |
|
||||
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области понятие клеточного автомата имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое понятие клеточного автомата, клеточный автомат и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем