Лекция
Привет, Вы узнаете о том , что такое электрические цепи с внешним периодическим воздействием, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электрические цепи с внешним периодическим воздействием, коэффициент пульсации , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
Исследование, описанное в статье про электрические цепи с внешним периодическим воздействием, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электрические цепи с внешним периодическим воздействием, коэффициент пульсации и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Из статьи мы узнали кратко, но содержательно про электрические цепи с внешним периодическим воздействием
Электрической цепью с внешним периодическим воздействием называют такую электрическую цепь, хотя бы одна входная переменная которой (задающее напряжение или ток) является периодической функцией времени, а остальные либо также являются периодическими функциями времени, либо постоянными величинами.
Математическая модель такой цепи, представляет собой нормальную систему обыкновенных дифференциальных уравнений первого порядка, в матричной форме имеющую вид:
где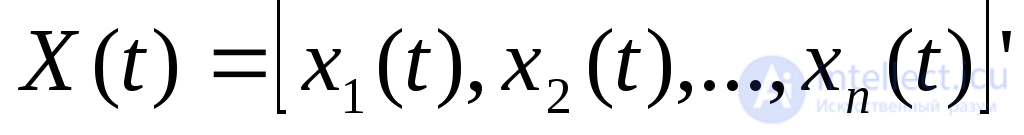 -одностолбцовая матрица (вектор) переменных состояния;
-одностолбцовая матрица (вектор) переменных состояния;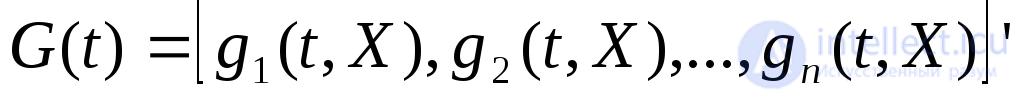 - n-мерная периодическая вектор-функция;Т -период внешнего воздействия.
- n-мерная периодическая вектор-функция;Т -период внешнего воздействия.
Для линейных электрических цепей с постоянными сосредоточенными параметрами математическая модель (2.1) может быть представлена в виде:
где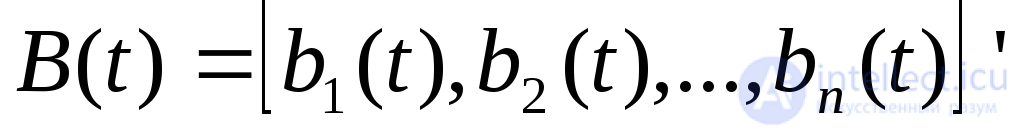 -n-мерная периодическая вектор-функция внешних воздействии;А -квадратная матрицап-гопорядка постоянных коэффициентов дифференциальных уравнений.
-n-мерная периодическая вектор-функция внешних воздействии;А -квадратная матрицап-гопорядка постоянных коэффициентов дифференциальных уравнений.
При математическом моделировании электрических цепей часто пользуются понятиями мгновенного и динамического состояний электрической цепи. Под мгновенным состоянием электрической цепи понимают совокупность значений всех переменных состояния в произвольный фиксированный момент времени. Об этом говорит сайт https://intellect.icu . Под динамическим состоянием (движением, динамикой)подразумевают поведение переменных состояния в течение некоторого временного интервала, в частности, сколь угодно большого. В зависимости от характера изменения переменных состояния, движения электрических цепей подразделяют на стационарные и нестационарные.При стационарной динамике переменные состояния либо не изменяются во времени (стационарные состояния статического типа), либо изменяются периодически (стационарные состояния периодического типа). Все остальные динамические состояния относятся к нестационарным. Среди них, в свою очередь, выделяют переходные состояния {переходные процессы) и стохастические (хаотические)состояния. К переходным относятся такие нестационарные состояния, которые в некоторый момент времени заканчиваются установлением стационарной динамики. Если же переменные состояния изменяются случайным образом (хаотически) и не устанавливается никакое стационарное состояние, то такая динамика носит название стохастической (хаотической).
Для линейных электрических цепей с постоянными сосредоточенными параметрами характерно наличие одного стационарного состояния, которое часто называют установившимся. В случае цепей с внешним постоянным воздействием это стационарное состояние статического типа, а для цепей с внешним периодическим воздействием - стационарное состояние периодического типа, период которого совпадает с периодом внешнего воздействия.
Понятие коэффициента пульсации.Пусть функция времениf(t) периодическая с периодом Г и удовлетворяет условиям Дирихле. В этом случае данную функцию можно представить в виде ряда Фурье:
где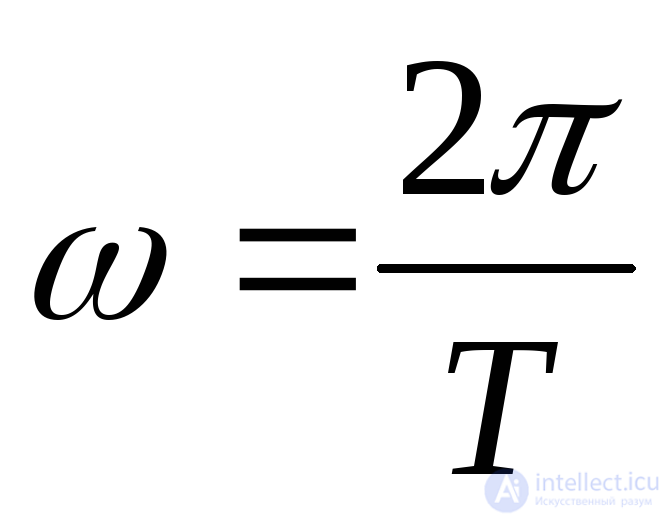 - круговая частота;
- круговая частота;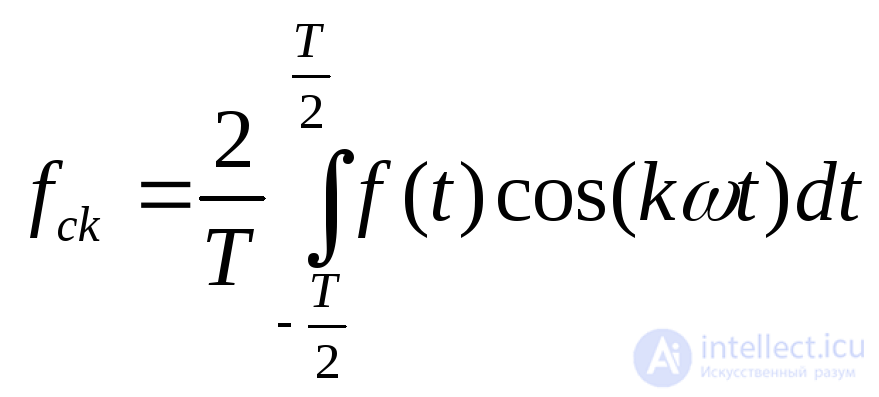 ,
,
Коэффициентам пульсации по k-ой гармонике называется величина, равная отношению амплитуды k-ой гармоники к постоянной составляющей:
С ростом порядкового номера амплитуды гармонических составляющих уменьшаются. Во многих случаях это позволяет с достаточной степенью точности представить периодическую функцию в виде суммы постоянной и первой гармонической составляющих. В силу данного обстоятельства при характеристике периодических функций коэффициент пульсации по первой гармонике используется чаще других.
+Вычисление коэффициента пульсации периодической функции по первой гармонике часто осуществляют, не прибегая к разложению функции в ряд Фурье, по формуле
где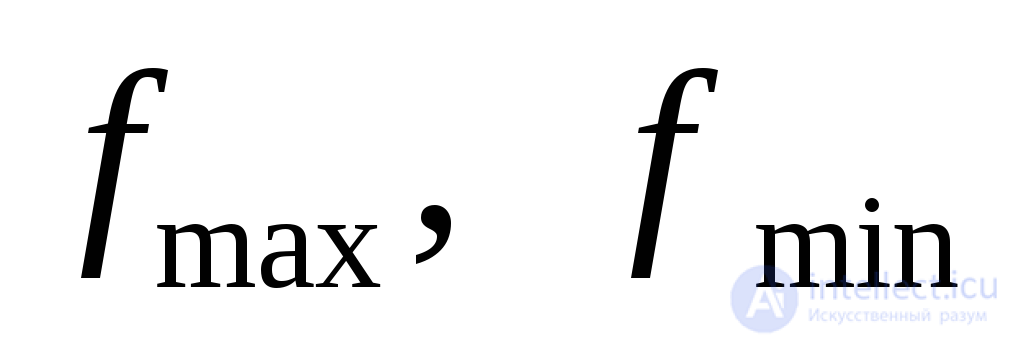 соответственно максимальное и минимальное значения функцииf (t)на периоде. Если функцияf(t)рассчитывается в дискретные моменты времени, то вычисление среднего значения можно приблизительно производить по формуле
соответственно максимальное и минимальное значения функцииf (t)на периоде. Если функцияf(t)рассчитывается в дискретные моменты времени, то вычисление среднего значения можно приблизительно производить по формуле
где M- количество точек дискретизации функцииf(t)на периоде.
Вау!! 😲 Ты еще не читал? Это зря!