каждой клетке; перемещение частиц в соответствии с правилами автомата.
трех направлений («вперед», «вправо», «влево»). При этом учитывается состояние N
модели.
где i, j – координаты текущей клетки, X – состояние соседних клеток. Об этом говорит сайт https://intellect.icu . Если при
последовательной проверке клеток встречается стенка, то все последующие клетки
считаются заполненными, так как они являются недоступными.
Найденные вероятности используются на втором этапе. Последовательно
проверяются три направления движения («вперед», или «в стороны»), если хотя бы
одно из них свободно – частица перемещается. Если три ближайшие клетки заняты –
частица передвигается «назад».
Таким образом, частицы перемещаются по клеткам автомата в соответствии со
следующими правилами:
• при возможности частица двигается вперед (по отношению к некоторому
заданному направлению);
• если движение вперед невозможно, частица двигается вправо/влево или назад;
• наличие в каком-либо направлении других частиц или стен уменьшает
вероятность движения частицы в этом направлении.
задания
21
• Поместить на поле несколько рыб. Позволить им размножиться. Далее
поместить несколько акул. Изменить параметры популяции акул так, чтобы
рыбы вымерли. Привести значения этих параметров.
• То же самое, но добиться вымирания акул, изменяя параметры рыб, привести
значения этих параметров.
9.3. Линейный автомат
• Определите размерность получаемого узора.
• Исследуйте влияние параметров на размерность и конфигурацию узора,
постройте и сохраните для отчета соответствующие графики.
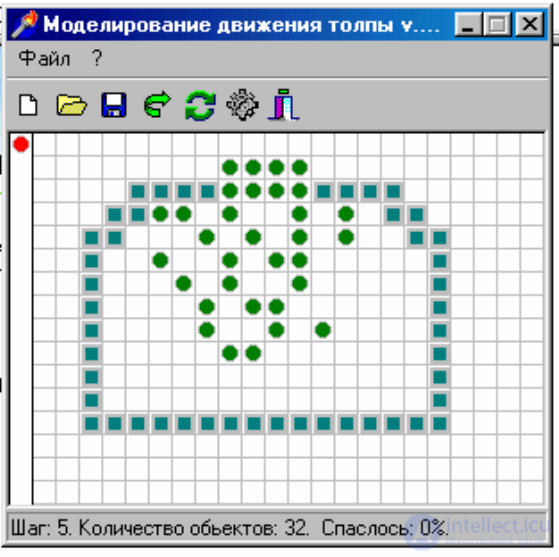
9.4. Клеточный автомат, моделирующий движение толпы
• Cоздайте замкнутую область (17х12 клеток), с единственным выходом из 3
клеток. Постройте зависимости числа вышедших людей от времени для разных
значений плотности начального заполнения. Найдите время полного выхода
людей и проанализируйте ее зависимость от времени.
• Повторите построения для различной ширины N выхода, где N меняется от
2 до 10. Постройте зависимости времени полного выхода людей от ширины
выхода.
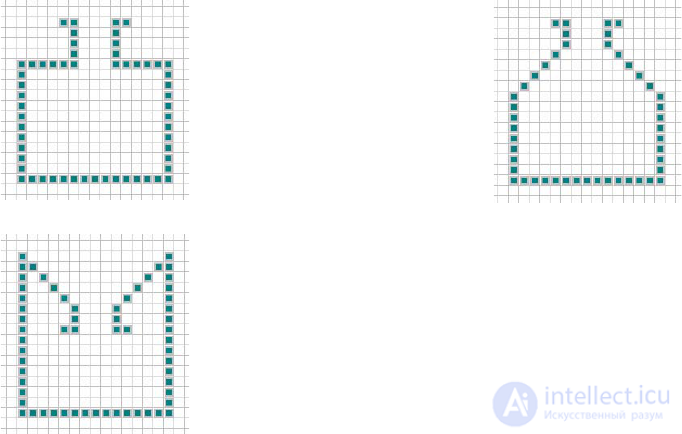
• Создайте область, похожую на бутылку с «резкими» краями (рис. 17а).
Постройте зависимости времени выхода всех людей из области от плотности
начального заполнения и от ширины выхода.
• Создайте область, похожую на бутылку (рис. 17б). Постройте зависимость
времени выхода всех людей из области от плотности начального заполнения и от
ширины выхода. Сравните результаты, с полученными в предыдущем задании.
• Создайте область, похожую на чернильницу «непроливайку» (рис. 17в).
Постройте зависимость времени выхода всех людей из области от плотности
начального заполнения и от ширины выхода. Сравните результаты, с
полученными в предыдущих заданиях.
Рис 17. Области для исследования
Контрольные вопросы.
1) Какова «скорость света» в игре «Жизнь» Конвея?
2) Какова скорость планера?
3) Из скольких клеток состоит минимальная устойчивая конфигурация?
4) Почему популяция в «Аква-Торе» при бесконечном количестве пищи растет не
безгранично?
5) Как вычисляется фрактальная размерность?
6) Чему равна размерность ковра Серпинского?
7) Какие из представленных клеточных автоматов являются обратимыми и
почему?
8) Найдите аналитическое решение уравнения Ферхюльста
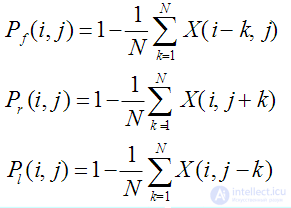 (5)
(5)


Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем